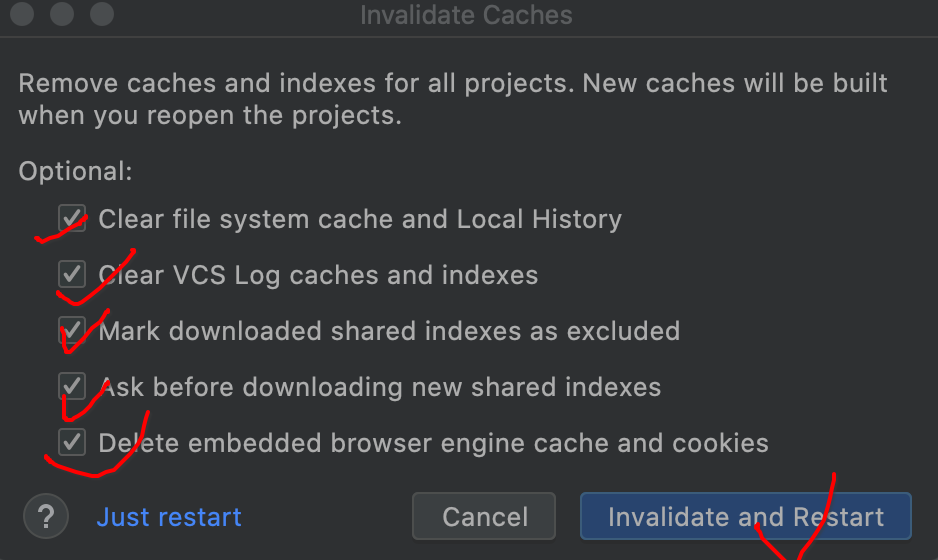
1、浮点数的表示方法
假设有以下小数,它表示的十进制数是多少呢?
00000000 00000000 00000000 1010.1010
1*2^3 + 1*2^1 + 1*2^-1 + 1*2^-3 = 10.625
1010.1010可以用科学计数法来表示为1.0101010 * 2^3。关于科学计数法再举个例子0.10101用科学计数法表示为1.10101 * 2^-1。
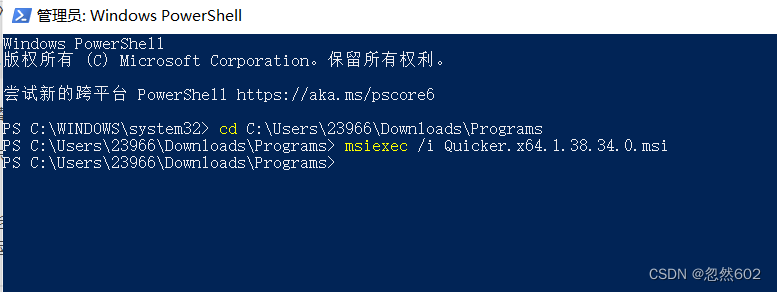
计算机中浮点数的存储方法如下:
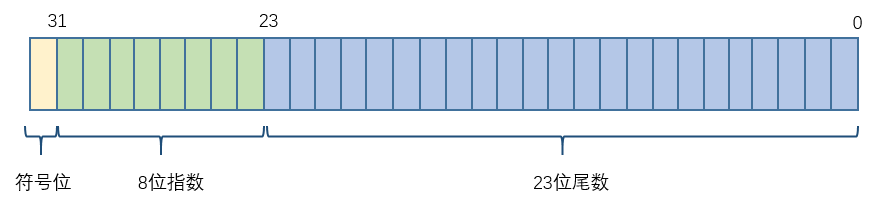
32位被划分为三个部分:1位符号、8位指数以及23位尾数。这里的符号指数尾数都是什么呢?
- 符号就是浮点数的正负,正数为0,负数为1;
- 指数位是科学计数法表示的浮点二进制数的指数,由于指数可能有正负,这里的处理方式是将指数加上127再存到这8位中,相应的读取时要减去127;
- 尾数位是科学计数法表示的浮点二进制数的小数部分;
- 由于科学计数法第一位一定是1,所以这一位存储时被舍弃,读取的时候会加上。
以10.625为例,它的二进制数表示为1.0101010 * 2^3,它在计算机中存储为:
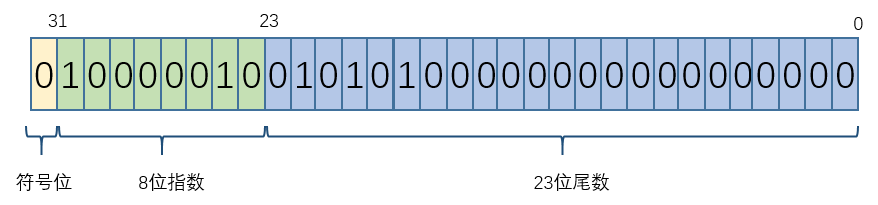
反过读取其表示的值:
(-1)^0 * (1 + 0.010101) * 2^(130 - 127) = 1.010101 * 2^3 = 1010.101
要注意这里的2^3并不是8,指的是小数点向后移动3位!如果是1.0*2^3,它表示小数点向右移动三位,表示的二进制数为0b1000,对应的十进制数为2^3=8。这很重要,看不懂就没法理解下一节的内容。
2、浮点数的范围
浮点数能表示的值的范围是多少呢?
这里有几个规定:
| 指数 | 尾数 | 值 | binary |
|---|---|---|---|
| 255 | 0 | +/- ∞ | 0 11111111 00000000000000000000000 |
| 255 | 非0 | NaN(not a number) | 0 11111111 00000000000000000000001 |
指数为255时对应的值是无穷以及NaN,所以浮点数指数不能取到255,其范围是-127 ~ 127。值的大小取决于指数,所以二进制范围约为-(1*2^127) ~ (1 * 2^127),十进制范围约为-2^127 ~ 2^127
用一个数轴来表示32位浮点数能够表示的十进制范围:

看到中间有一段十进制范围-2^-127 ~ 2^-127,这中间是浮点数所不能表示的部分即精度不够的地方,计算方式同上。
3、浮点数的精度
网上很多博文说浮点数的精度为6 - 7位,我看了很是不解!
明明浮点数能表示的十进制最小值可以大约是2^-127,你说它的精度是6-7位不是胡说吗?
我的理解是这样:
浮点数不为0最小值,或者说是最小单位长度为:
0 00000000 00000000000000000000001
对应的二进制数为(1+2^-23)*2^-127,而这个值的精度取决于括号中的2^-23,由于32位浮点数只有23位表示尾数,所以精度最高只能达到2^-23。
将二进制数2^-23 转化为十进制 为 10^(-6.9),也就是十进制小数点后6位,所以说精度是6位。
以上说法还比较抽象,这里举个例子,
0 01111111 00000000000000000000001 = (1 + 2^-23) * 2^0 = 0b1.00000000000000000000001
0 01111111 00000000000000000000010 = (1 + .....) * 2^0 = 0b1.00000000000000000000010
0 01111111 00000000000000000000011 = (1 + .....) * 2^0 = 0b1.00000000000000000000011
每次变化都是以最小单位0b0.00000000000000000000001来变化,而这个值对应的十进制数也就是2^-23约为10^(-6.9),所以精度为6位。
以上是我对浮点数的理解,如果错误欢迎指出。