实现二叉排序树

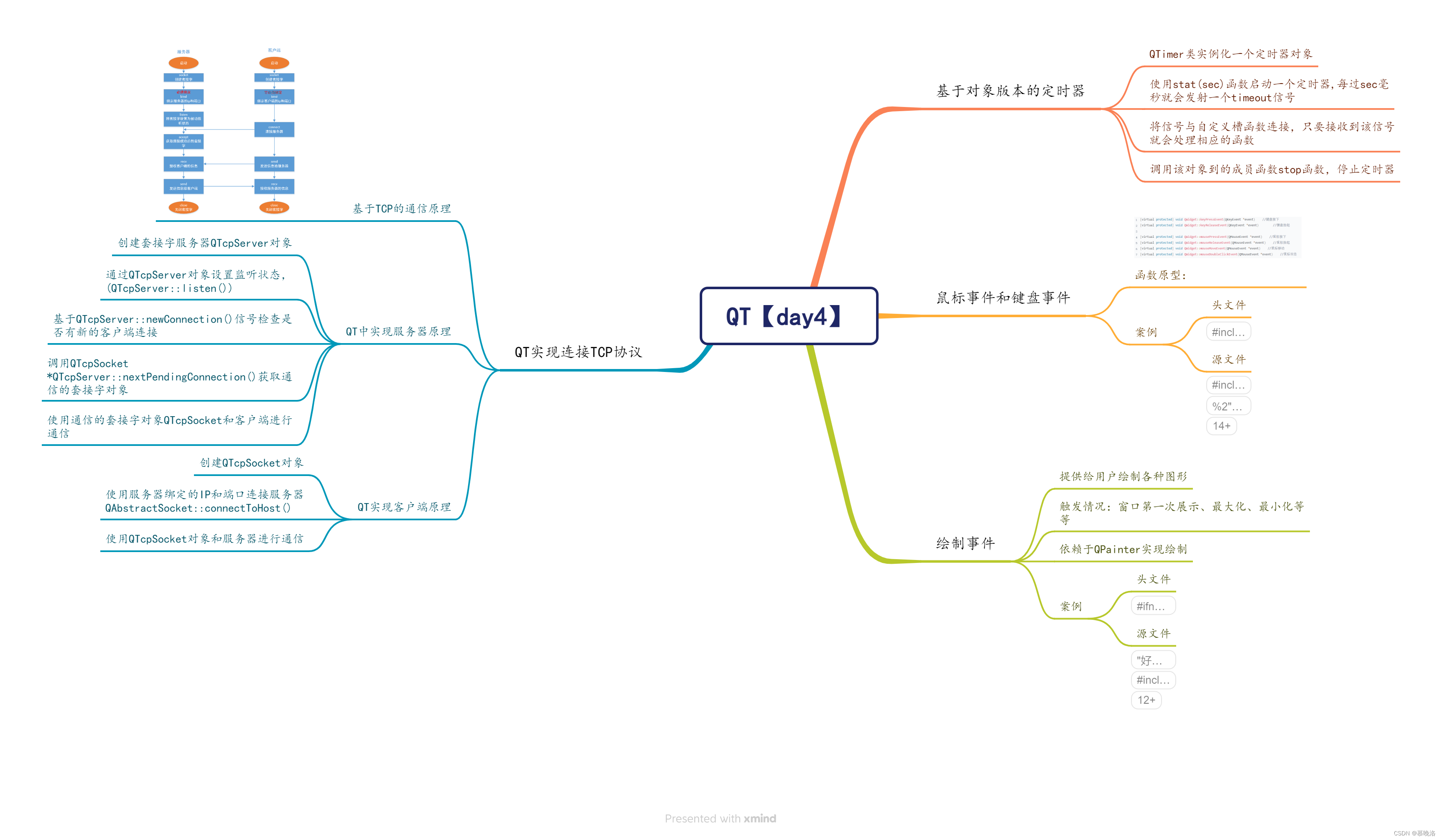
一：二叉树和二叉搜索树

二叉树中的节点最多只能有两个子节点：一个是左侧子节点，另一个是右侧子节点。这个定义有助于我们写出更高效地在树中插入、查找和删除节点的算法，二叉树在计算机科学中的应用非常广泛。
**二叉搜索树（BST）**是二叉树的一种，但是只允许你在左侧节点存储（比父节点）小的值，在右侧节点存储（比父节点）大的值。

二：实现二叉搜索树

2.1 创建Node类表示二叉搜索树中的每个节点

    //二叉树的存储结构为
    class Node
    {
      constructor(data, left, right)
      {
        this.data = data
        this.left = left
        this.right = right
        //若有相同的元素插入节点，就放弃插入，count++
        this.count = 1
      }
    }

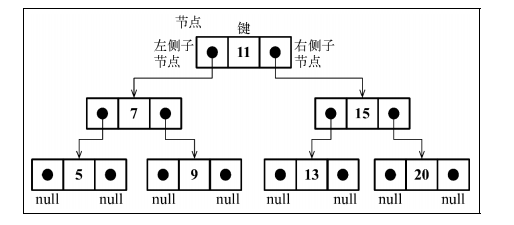
该图为二叉搜索树数据结构的组织方式，对于树，我们使用两个指针，一个指向左侧子节点，一个指向右侧右节点

2.2 创建BSTree 类的基本结构

class BSTree {
    constructor() {
        this.root = null;
    }
 
    // 删除一个节点
    _removeNode(node, data) {
       
    }
 
    // 删除给定的数据节点
    remove(data) {
        this.root = this._removeNode(this.root, data);
    }
 
    // 向二叉树中插入节点
    insert(data) {
        
    }
 
    // 寻找给定数据的节点
    find(data) {
        
    }
 
    // 获得最小值的节点
    getMinNode(node = this.root) {
        
    }
 
    // 获得最大值的节点
    getMaxNode(node = this.root) {
        
    }
}

2.3 实现insert()方法

//向二叉树插入节点
insert (data)
{
    let newNode = new Node(data, null, null)
    //更新根节点的值
    if (this.root === null) {
        this.root = newNode
    } else {
        //更新当前节点的值
        let currentNode = this.root
        //父节点就是空
        let parentNode = null
        while (true) {
            //更新父节点
            parentNode = currentNode
            //判断插入节点值在左子树还是右子树
            if (newNode.data < currentNode.data) {
                //更新当前节点
                currentNode = currentNode.left
                if (!currentNode) {
                    parentNode.left = newNode
                    break
                }
            }

            else if (newNode.data > currentNode.data) {
                currentNode = currentNode.right
                if (!currentNode) {
                    parentNode.right = newNode
                    break
                }
            }

            else if (newNode.data === currentNode.data) {
                //如果相同数据 count++ 不做处理
                currentNode.count++
                break
            }
        }
    }
}

首先创建一个新的节点newNode，该节点包含要插入的数据
检查根节点是否为空，若为空，说明这是第一个插入的节点，将根节点指向newNode
如果根节点不为空，则需要找到合适的位置插入该节点
初始化当前节点currentNode为根节点this.root，并且初始化父节点parentNode为空
进入循环，直到找到合适的位置插入节点或者遇到相同的数据
在每次循环中，更新父节点parentNode为当前节点currentNode
判断要插入的节点值和当前节点值的大小关系
- 如果要插入的节点值小于当前节点值，说明要插入的节点应该在当前节点的左子树中
  - 更新当前节点为当前节点的左子节点 currentNode.left
  - 如果当前节点的左子节点为空，说明找到了插入位置，将新节点 newNode 设置为当前节点的左子节点，并且跳出循环
- 如果要插入的节点值大于当前节点值，说明要插入的节点应该在当前节点的右子树中
  - 更新当前节点为当前节点的右子节点 currentNode.right
  - 如果当前节点的右子节点为空，说明找到了插入位置，将新节点 newNode 设置为当前节点的右子节点，并且跳出循环
- 如果要插入的节点值等于当前节点值，说明要插入的节点与当前节点的值相同。
  - 将当前节点的计数器 count 加一，表示重复出现的次数。
  - 跳出循环。

2.4 实现find()方法

//寻找给定数据的节点
find (data)
{
    let currentNode = this.root
    while (currentNode) {
        if (currentNode.data == data) {
            return currentNode
        } else if (currentNode.data < data) {
            currentNode = currentNode.right
        } else {
            currentNode = currentNode.left
        }
    }
    return null
}

2.5 实现getMinNode()和getMaxNode()方法

//获取最小值
getMinNode (node = this.root)
{
    let currentNode = node
    while (currentNode.left) {
        currentNode = currentNode.left
    }
    return currentNode
}

//获取最大值
getMaxNode (node = this.root)
{
    let currentNode = node
    while (currentNode.right) {
        currentNode = currentNode.right
    }
    return currentNode
}

2.6 实现remove()方法

//删除节点，实例中不应调用
_removeNode (node, data)
{
    if (node === null) {
        return null
    }
    //找到要删除的节点的了 
    if (data === node.data) {
        //分三种情况
        //1. 要删除的节点为叶子结点 
        if (node.left === null && node.right === null) {
            return null
        }

        //2. 没有左子节点的节点
        if (node.left === null) return node.right

        //   没有右子节点的节点
        if (node.right === null) return node.left


        //3.有两个子节点的节点
        //找到待删除节点的右子树的最小值赋值给临时节点tmpNode
        //将tmpNode赋值给node 就说明用右子树的最小值来代替待删除节点
        let tmpNode = this.getMinNode(node.right)
        //tmpNode赋值给待删除节点
        node.data = tmpNode.data
        //删除临时节点
        node.right = this._removeNode(node.right, tmpNode.data)
        return node
    } else if (data < node.data) {  //待删除节点在左子树上
        node.left = this._removeNode(node.left, data)
        return node
    } else { //待删除节点在右子树上
        node.right = this._removeNode(node.right, data)
        return node
    }
}
//删除节点
remove (data)
{
    this.root = this._removeNode(this.root, data);
}

代码接收两个参数：data表示待删除的节点的值，node表示当前递归调用的节点。
如果待删除节点的值等于当前节点的值（data == node.data），则进入条件判断。
如果当前节点是叶子节点（即没有左子节点和右子节点），则将其置为null，表示删除该节点。
如果当前节点只有左子节点而没有右子节点，则返回其左子节点，将其作为当前节点的父节点的新子节点。
如果当前节点只有右子节点而没有左子节点，则返回其右子节点，将其作为当前节点的父节点的新子节点。
如果当前节点既有左子节点又有右子节点，则需要找到待删除节点的右子树上的最小值来替代待删除节点。
通过调用getMinNode(node.right)方法，找到右子树上的最小值所在的节点，并将其赋值给临时节点tmpNode。
将临时节点tmpNode的值复制到待删除节点node，相当于用右子树上的最小值替代了待删除节点。
再次递归调用_removeNode()方法，传入当前节点的右子节点和临时节点的值，以删除右子树上的最小值节点。
最后，返回当前节点node，表示删除操作完成。
如果待删除节点的值小于当前节点的值（data < node.data），则递归调用_removeNode()方法，传入当前节点的左子节点和待删除节点的值，以在左子树上继续删除操作。
如果待删除节点的值大于当前节点的值，则递归调用_removeNode()方法，传入当前节点的右子节点和待删除节点的值，以在右子树上继续删除操作。
最终，整个删除操作完成后，返回当前节点node，并将其作为父节点的新子节点。

三：测试数据

    let myTree = new BSTree();

    myTree.insert(20);
    myTree.insert(13);
    myTree.insert(7);
    myTree.insert(9);
    myTree.insert(15);
    myTree.insert(14);
    myTree.insert(42);
    myTree.insert(22);
    myTree.insert(21);
    myTree.insert(24);
    myTree.insert(57);

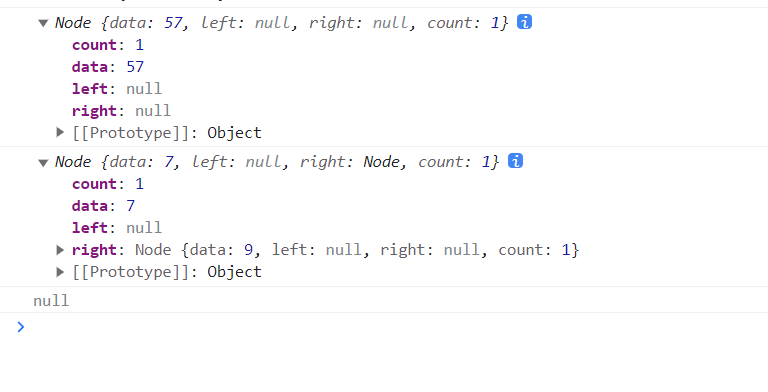
    console.log(myTree.getMaxNode());  
    console.log(myTree.getMinNode()); 
    myTree.remove(7)
    console.log(myTree.find(7));

四：全部代码

    //二叉树的存储结构为
    class Node
    {
      constructor(data, left, right)
      {
        this.data = data
        this.left = left
        this.right = right
        //若有相同的元素插入节点，就放弃插入，count++
        this.count = 1
      }
    }

    //二叉排序树
    class BSTree
    {
      constructor()
      {
        this.root = null
      }

      //向二叉树插入节点
      insert (data)
      {
        let newNode = new Node(data, null, null)
        //更新根节点的值
        if (this.root === null) {
          this.root = newNode
        } else {
          //更新当前节点的值
          let currentNode = this.root
          //父节点就是空
          let parentNode = null
          while (true) {
            //更新父节点
            parentNode = currentNode
            //判断插入节点值在左子树还是右子树
            if (newNode.data < currentNode.data) {
              //更新当前节点
              currentNode = currentNode.left
              if (!currentNode) {
                parentNode.left = newNode
                break
              }
            }

            else if (newNode.data > currentNode.data) {
              currentNode = currentNode.right
              if (!currentNode) {
                parentNode.right = newNode
                break
              }
            }

            else if (newNode.data === currentNode.data) {
              //如果相同数据 count++ 不做处理
              currentNode.count++
              break
            }
          }
        }
      }

      //获取最小值
      getMinNode (node = this.root)
      {
        let currentNode = node
        while (currentNode.left) {
          currentNode = currentNode.left
        }
        return currentNode
      }

      //获取最大值
      getMaxNode (node = this.root)
      {
        let currentNode = node
        while (currentNode.right) {
          currentNode = currentNode.right
        }
        return currentNode
      }

      //寻找给定数据的节点
      find (data)
      {
        let currentNode = this.root
        while (currentNode) {
          if (currentNode.data == data) {
            return currentNode
          } else if (currentNode.data < data) {
            currentNode = currentNode.right
          } else {
            currentNode = currentNode.left
          }
        }
        return null
      }
      //删除节点，实例中不应调用
      _removeNode (node, data)
      {
        if (node === null) {
          return null
        }
        //找到要删除的节点的了 
        if (data === node.data) {
          //分三种情况
          //1. 要删除的节点为叶子结点 
          if (node.left === null && node.right === null) {
            return null
          }

          //2. 没有左子节点的节点
          if (node.left === null) return node.right

          //   没有右子节点的节点
          if (node.right === null) return node.left


          //3.有两个子节点的节点
          //找到待删除节点的右子树的最小值赋值给临时节点tmpNode
          //将tmpNode赋值给node 就说明用右子树的最小值来代替待删除节点
          let tmpNode = this.getMinNode(node.right)
          //tmpNode赋值给待删除节点
          node.data = tmpNode.data
          //删除临时节点
          node.right = this._removeNode(node.right, tmpNode.data)
          return node
        } else if (data < node.data) {  //待删除节点在左子树上
          node.left = this._removeNode(node.left, data)
          return node
        } else { //待删除节点在右子树上
          node.right = this._removeNode(node.right, data)
          return node
        }
      }
      //删除节点
      remove (data)
      {
        this.root = this._removeNode(this.root, data);
      }
    }

    let myTree = new BSTree();

    myTree.insert(20);
    myTree.insert(13);
    myTree.insert(7);
    myTree.insert(9);
    myTree.insert(15);
    myTree.insert(14);
    myTree.insert(42);
    myTree.insert(22);
    myTree.insert(21);
    myTree.insert(24);
    myTree.insert(57);
    console.log(myTree);