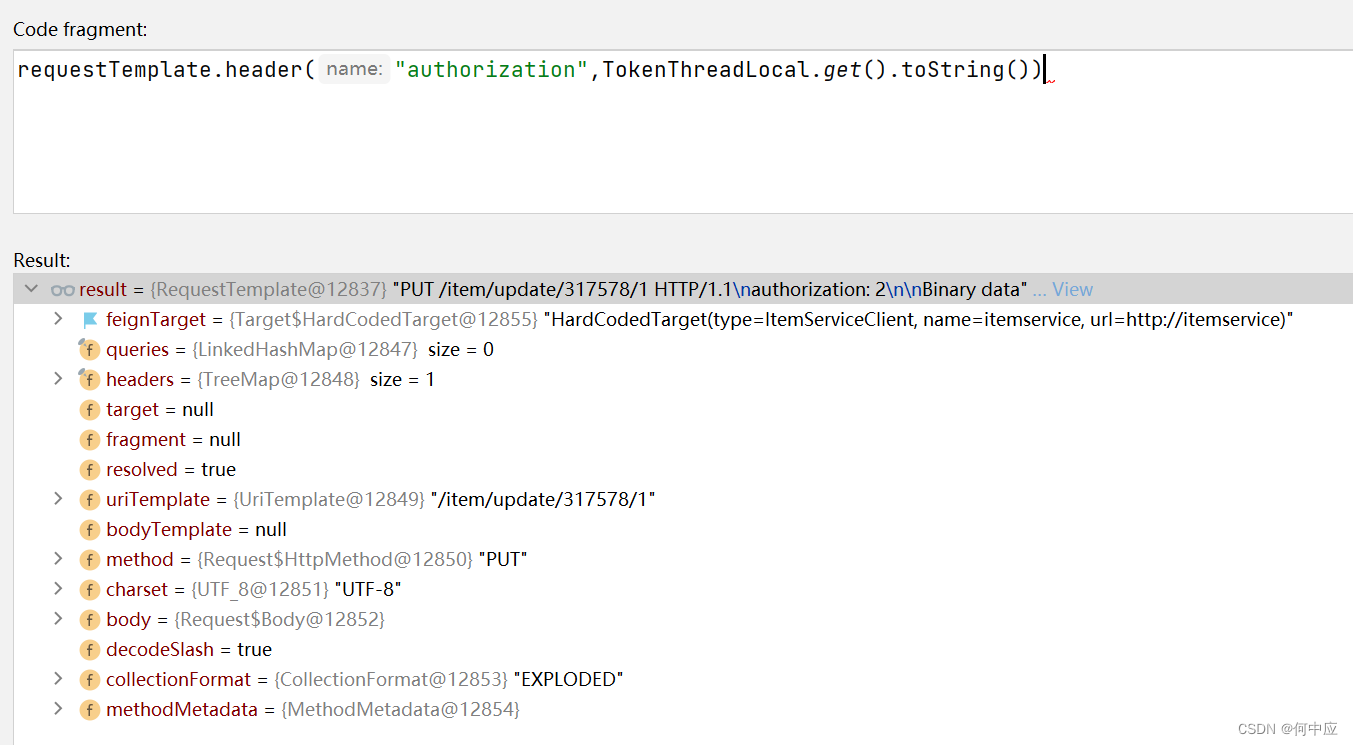
题目

给定一张n个点的带权无向图，点从0~n-1标号，求起点0到终点n-1的最短Hamilton路径。Hamilton路径的定义是从0到n-1不重不漏地经过每个点恰好一次。

输入格式

第—行输入整数n。
接下来n行每行n个整数，其中第i行第j个整数表示点i到j的距离(记为a[i.i])。对于任意的, y,z，数据保证a[x,x]=0，a[x,y]=a[y,x]并且a[x,y]+aly,z]>=a[x,z]。

输出格式

输出一个整数，表示最短Hamilton路径的长度。

数据范围

1 ≤n ≤200≤a[i,j≤107

• 输入样例

5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0

• 输出样例:

18

题解

import java.util.Arrays;
import java.util.Scanner;

/**
 * @author akuya
 * @create 2023-07-28-20:56
 */
public class hamiltion {
    static int N=20;
    static int M=1<<N;
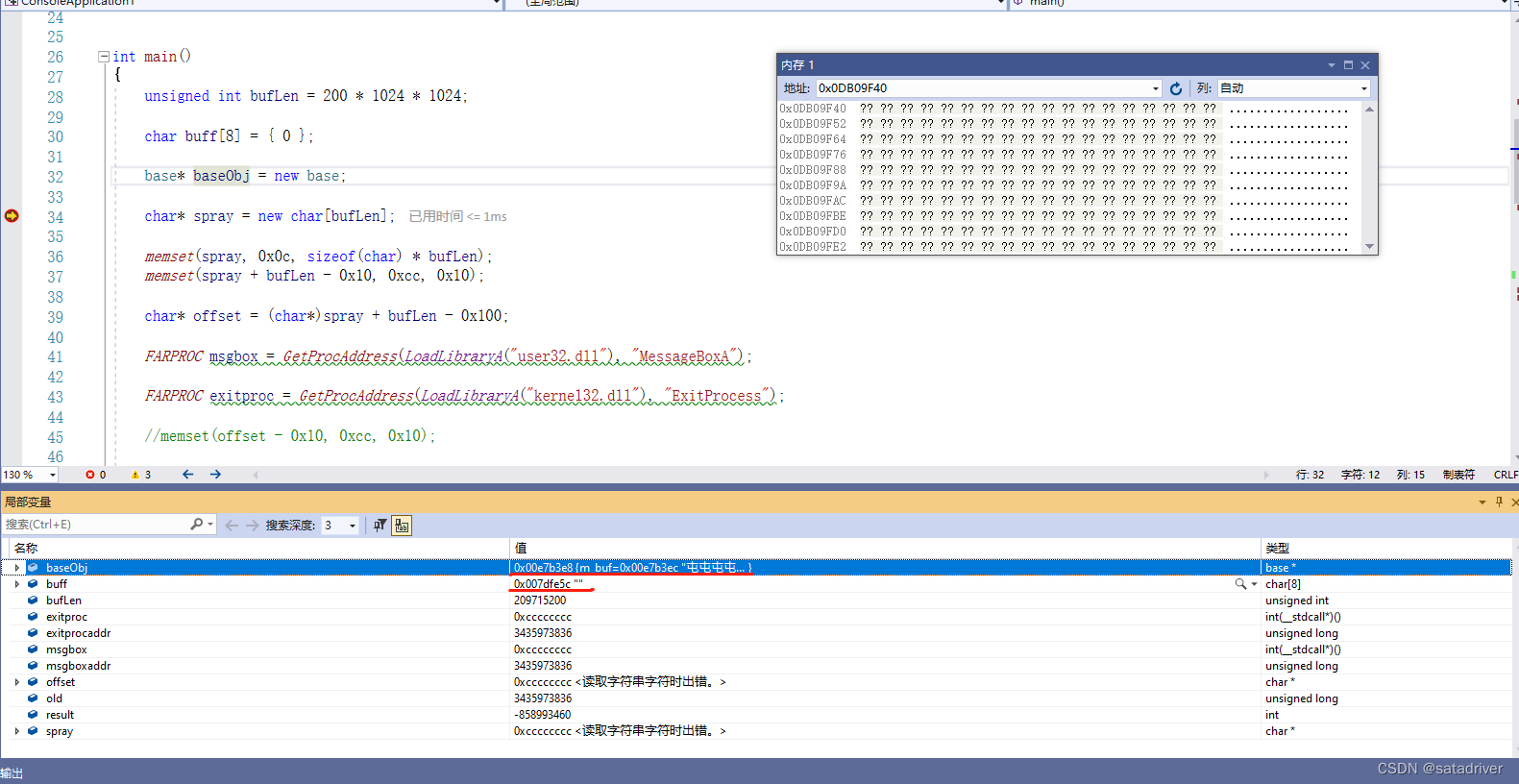
    static int n;
    static int w[][]=new int[N][N];
    static int f[][]=new int[M][N];

    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        n=scanner.nextInt();
        for(int i=0;i<n;i++)
            for (int j = 0; j < n; j++)
                w[i][j]=scanner.nextInt();

        for(int i=0;i<M;i++){
            Arrays.fill(f[i],0x3f);
        }

        f[1][0]=0;
        for(int i=0;i<1<<n;i++)
            for(int j=0;j<n;j++)
                if((i>>j&1)!=0)
                    for(int k=0;k<n;k++)
                        if(((i-(1<<j))>>k&1)!=0)
                            f[i][j]=Math.min(f[i][j],f[i-(1<<j)][k]+w[k][j]);


        System.out.println(f[(1<<n)-1][n-1]);


    }
}

思路

本题同样是状态压缩类的动态规划，具体思路如下图

i代表走过的点，状态转移用到达j点的倒数第二个点，转移方程得出为

f[i][j]=Math.min(f[i][j],f[i-(1<<j)][k]+w[k][j]);

注意边界条件即可