DFS之连通性模型
dfs 与 bfs都能判断连通性 而且bfs可以得出最短距离 而dfs不可以 dfs 代码比较简洁
迷宫
一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 n∗nn∗n 的格点组成,每个格点只有2种状态,.和#,前者表示可以通行后者表示不能通行。
同时当Extense处在某个格点时,他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上,Extense想要从点A走到点B,问在不走出迷宫的情况下能不能办到。
如果起点或者终点有一个不能通行(为#),则看成无法办到。
注意:A、B不一定是两个不同的点。
输入格式
第1行是测试数据的组数 k,后面跟着 k 组输入。
每组测试数据的第1行是一个正整数 n,表示迷宫的规模是 n∗n 的。
接下来是一个 n∗n 的矩阵,矩阵中的元素为.或者#。
再接下来一行是 4 个整数 ha,la,hb,lb,描述 A 处在第 ha 行, 第 la列,BB 处在第 hb 行, 第 lb 列。
注意到 ha,la,hb,lb全部是从 0 开始计数的。
输出格式
k行,每行输出对应一个输入。
能办到则输出“YES”,否则输出“NO”。
数据范围
1≤n≤100
输入样例:
2
3
.##
..#
#..
0 0 2 2
5
.....
###.#
..#..
###..
...#.
0 0 4 0
输出样例:
YES
NO#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=110;
char s[N][N];
bool st[N][N];
int n;
int a,b,a1,b1;
int dx[]={0,0,-1,1},dy[]={1,-1,0,0};
bool dfs(int a,int b)
{
if(s[a][b]=='#') return false;
if(a==a1&&b==b1) return true;
st[a][b]=true;
for(int i=0;i<4;i++)
{
int x=a+dx[i],y=b+dy[i];
if(x<0||x>=n||y<0||y>=n) continue;
if(st[x][y])continue;
if(dfs(x,y)) return true;
}
return false;
}
int main()
{
int t;cin>>t;
while(t--)
{
memset(st,0,sizeof st);
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++) cin>>s[i][j];
cin>>a>>b>>a1>>b1;
if(dfs(a,b)) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
}红与黑
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。
你站在其中一块黑色的瓷砖上,只能向相邻(上下左右四个方向)的黑色瓷砖移动。
请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
输入格式
输入包括多个数据集合。
每个数据集合的第一行是两个整数 W 和 H,分别表示 x 方向和 y 方向瓷砖的数量。
在接下来的 H 行中,每行包括 W 个字符。每个字符表示一块瓷砖的颜色,规则如下
1)‘.’:黑色的瓷砖;
2)‘#’:红色的瓷砖;
3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。
当在一行中读入的是两个零时,表示输入结束。
输出格式
对每个数据集合,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
数据范围
1≤W,H≤20
输入样例:
6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
0 0
输出样例:
45#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=72;
char s[N][N];
bool st[N][N];
int n,m,cnt;
int dx[]={0,0,-1,1},dy[]={1,-1,0,0};
void dfs(int x,int y)
{
cnt++;
st[x][y]=1;
for(int i=0;i<4;i++)
{
int x1=x+dx[i],y1=y+dy[i];
if(x1<0||x1>=n||y1<0||y1>=m) continue;
if(st[x1][y1]) continue;
if(s[x1][y1]!='.') continue;
dfs(x1,y1);
}
}
int main()
{
while(cin>>m>>n)
{
cnt=0;
if(n==0&&m==0) break;
int x,y;
memset(st,0,sizeof st);
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
cin>>s[i][j];
if(s[i][j]=='@')
{
x=i,y=j;
}
}
dfs(x,y);
cout<<cnt<<endl;
}
return 0;
}#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 25;
int n, m;
char g[N][N];
bool st[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dfs(int x, int y)
{
int cnt = 1;
st[x][y] = true;
for (int i = 0; i < 4; i ++ )
{
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= n || b < 0 || b >= m) continue;
if (g[a][b] != '.') continue;
if (st[a][b]) continue;
cnt += dfs(a, b);
}
return cnt;
}
int main()
{
while (cin >> m >> n, n || m)
{
for (int i = 0; i < n; i ++ ) cin >> g[i];
int x, y;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
if (g[i][j] == '@')
{
x = i;
y = j;
}
memset(st, 0, sizeof st);
cout << dfs(x, y) << endl;
}
return 0;
}DFS之搜索顺序
马走日
需要恢复现场
马在中国象棋以日字形规则移动。
请编写一段程序,给定 n∗m 大小的棋盘,以及马的初始位置 (x,y),要求不能重复经过棋盘上的同一个点,计算马可以有多少途径遍历棋盘上的所有点。
输入格式
第一行为整数 T,表示测试数据组数。
每一组测试数据包含一行,为四个整数,分别为棋盘的大小以及初始位置坐标 n,m,x,y
输出格式
每组测试数据包含一行,为一个整数,表示马能遍历棋盘的途径总数,若无法遍历棋盘上的所有点则输出 0。
数据范围
1≤T≤9
1≤m,n≤9
1≤n×m≤28
0≤x≤n−1
0≤y≤m−1
输入样例:
1
5 4 0 0
输出样例:
32 
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=12;
bool st[N][N];
int n,m,x,y;
int cnt=0;
int dx[]={-2,-1,1,2,2,1,-1,-2};
int dy[]={1,2,2,1,-1,-2,-2,-1};
int ans=0;
//用cnt表示走过的格字数
void dfs(int x,int y,int cnt)
{
if(cnt==n*m)
{
ans++;
return ;
}
st[x][y]=1;
for(int i=0;i<8;i++)
{
int x1=x+dx[i],y1=y+dy[i];
if(x1<0||x1>=n||y1<0||y1>=m) continue;
if(st[x1][y1]) continue;
//是加1 千万不要写成 cnt++;
dfs(x1,y1,cnt+1);
//恢复现场
st[x1][y1]=false;
}
}
int main()
{
int t;cin>>t;
while(t--)
{
memset(st,0,sizeof st);
cin>>n>>m>>x>>y;
ans=0;
dfs(x,y,1);
cout<<ans<<endl;
}
}单词接龙
单词接龙是一个与我们经常玩的成语接龙相类似的游戏。
现在我们已知一组单词,且给定一个开头的字母,要求出以这个字母开头的最长的“龙”,每个单词最多被使用两次。
在两个单词相连时,其重合部分合为一部分,例如 beast 和 astonish ,如果接成一条龙则变为 beastonish。
我们可以任意选择重合部分的长度,但其长度必须大于等于1,且严格小于两个串的长度,例如 at 和 atide 间不能相连。
输入格式
输入的第一行为一个单独的整数 n 表示单词数,以下 n 行每行有一个单词(只含有大写或小写字母,长度不超过20),输入的最后一行为一个单个字符,表示“龙”开头的字母。
你可以假定以此字母开头的“龙”一定存在。
输出格式
只需输出以此字母开头的最长的“龙”的长度。
数据范围
n≤20
单词随机生成。
输入样例:
5
at
touch
cheat
choose
tact
a
输出样例:
23
提示
连成的“龙”为 atoucheatactactouchoose。
#include<iostream>
#include<cstring>
using namespace std;
const int N=22;
string word[N];//用每个单词是第几个 来建立关系
//用i j建立 这两个单词间是否i的后面 与j的开头 有重合部分 若有则取最小值
int g[N][N];
//用来表示单词总共用了几次
int used[N];
int n;
//全局变量求最大值
int ans=0;
//dragon 是现在字符串 last表示上一次用了那个单词用下标来表示
void dfs(string dragon,int last)
{
//取最大值
ans = max((int) dragon.size(), ans);
//用了一次 就++
used[last]++;
for(int i=0;i<n;i++)
{
//如果 g[last][i]>0 表示下标为last的字符串与下标是i的字符串可以接龙
//并且i这个单词使用不能超过两次
if(g[last][i]&&used[i]<2)
{
//不知道为什么 这样写里面就不行 因为如果这样写 会造成最初 刚进bfs的last不能被标记
//used[i]++;
dfs(dragon+word[i].substr(g[last][i]),i);
// used[i]--;
}
}
used[last]--;
}
int main()
{
cin>>n;
for(int i=0;i<n;i++) cin>>word[i];
char start;cin>>start;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
//因为单词最多可以使用两次 所有不需要用 i!=j这个限制条件 i与i也可以有联系
string a=word[i],b=word[j];
for(int k=1;k<=min(a.size(),b.size());k++)
{
if(a.substr(a.size()-k)==b.substr(0,k))
{
g[i][j]=k;
break;
}
}
}
}
for(int i=0;i<n;i++)
{
if(word[i][0]==start) dfs(word[i],i);
}
cout<<ans<<endl;
return 0;
}分成互质组
给定 n 个正整数,将它们分组,使得每组中任意两个数互质。
至少要分成多少个组?(组合问题)组合方式搜索
输入格式
第一行是一个正整数 n。
第二行是 n 个不大于10000的正整数。
输出格式
一个正整数,即最少需要的组数。
数据范围
1≤n≤10
输入样例:
6
14 20 33 117 143 175
输出样例:
3
#include<iostream>
#include<cstring>
using namespace std;
const int N = 10;
int n;
int a[N];//n个整数
int ans = N;//由于是求最小值,这里初始化为最大值
int g[N][N];//分组
int st[N];
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
bool check(int g[],int x,int start){
for(int i=0;i<start;i++){
if(gcd(g[i],x)>1) return false;
}
return true;
}
//当前要放在哪个分组;要放在该分组的第几个位置;从哪个位置开始选择元素【组合套路(定一个遍历顺序)】;当前已分组完毕的元素个数
void dfs(int gr,int gc,int start,int cnt){
if(gr>=ans) return;//剪枝 + 防止死循环
if(cnt==n) ans=gr;
bool flag=true;//从start开始找,是否有元素不能放到gr组中
for(int i=start;i<n;i++){
if(!st[i]&&check(g[gr],a[i],gc)){
st[i]=true;
g[gr][gc]=a[i];
dfs(gr,gc+1,i+1,cnt+1);
st[i]=false;
flag=false;
}
}
//新开一个分组
//由于dfs每层之间确定了顺序,所以期间是会有元素被漏掉的,【比如一开始你找的一串序列(1)是1,2,3,4 但是第二次(2)是1,3,4 很显然此时
//(2)还有一个3没有得到分组,需要从start=0开始再把它找出来! 因此这样做仿佛有点浪费时间呢!!】
//因此当所有元素都不能放进当前分组的时候 或者 当start=n-1了但是元素没有全部分组完毕时,要重新从start=0开始找,并且一定要有st数组!!!不然会把一个元素重复的分组!
if(flag) dfs(gr+1,0,0,cnt);
}
int main(){
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
//为什么一开始gr从1开始但是分组只开了10个呢?
//首先这样的话可以直接通过gr就得到当前分了多少组;其次由于ans初始化即为10,因此当打算开第10个分组时,会被弹回,数组不会越界
dfs(1,0,0,0);
cout<<ans;
return 0;
}
DFS之剪枝与优化
剪枝方式

小猫爬山
翰翰和达达饲养了 N 只小猫,这天,小猫们要去爬山。
经历了千辛万苦,小猫们终于爬上了山顶,但是疲倦的它们再也不想徒步走下山了(呜咕>_<)。
翰翰和达达只好花钱让它们坐索道下山。
索道上的缆车最大承重量为 W,而 N 只小猫的重量分别是 C1、C2……CN
当然,每辆缆车上的小猫的重量之和不能超过 W。
每租用一辆缆车,翰翰和达达就要付 1 美元,所以他们想知道,最少需要付多少美元才能把这 N 只小猫都运送下山?
输入格式
第 1行:包含两个用空格隔开的整数,N 和 W。
第 2..N+1 行:每行一个整数,其中第 i+1 行的整数表示第 i 只小猫的重量 Ci。
输出格式
输出一个整数,表示最少需要多少美元,也就是最少需要多少辆缆车。
数据范围
1≤N≤18
1≤Ci≤W≤10^8
输入样例:
5 1996
1
2
1994
12
29
输出样例:
2这样写是错误的 不能一辆一辆车的取考虑 应该去看看你所用的车辆中剩余空间能否载下这只小猫若不能则重新开一辆
#include<iostream>
#include<algorithm>
using namespace std;
const int N=20;
int a[N];
bool st[N];
int n,w;
int ans=0;
int max1=0x3f3f3f3;
void dfs(int sum,int num,int num1)
{
if(num>=max1) return ;
if(num1==n)
{
max1=min(max1,num);
return ;
}
for(int i=1;i<=n;i++)
{
if(!st[i])
{
st[i]=1;
if(sum+a[i]<=w)
{
dfs(sum+a[i],num,num1+1);
}
else
{
dfs(a[i],num+1,num1+1);
}
st[i]=0;
}
}
}
int main()
{
cin>>n>>w;
for(int i=1;i<=n;i++) cin>>a[i];
dfs(0,1,0);
cout<<max1<<endl;
return 0;
}正解
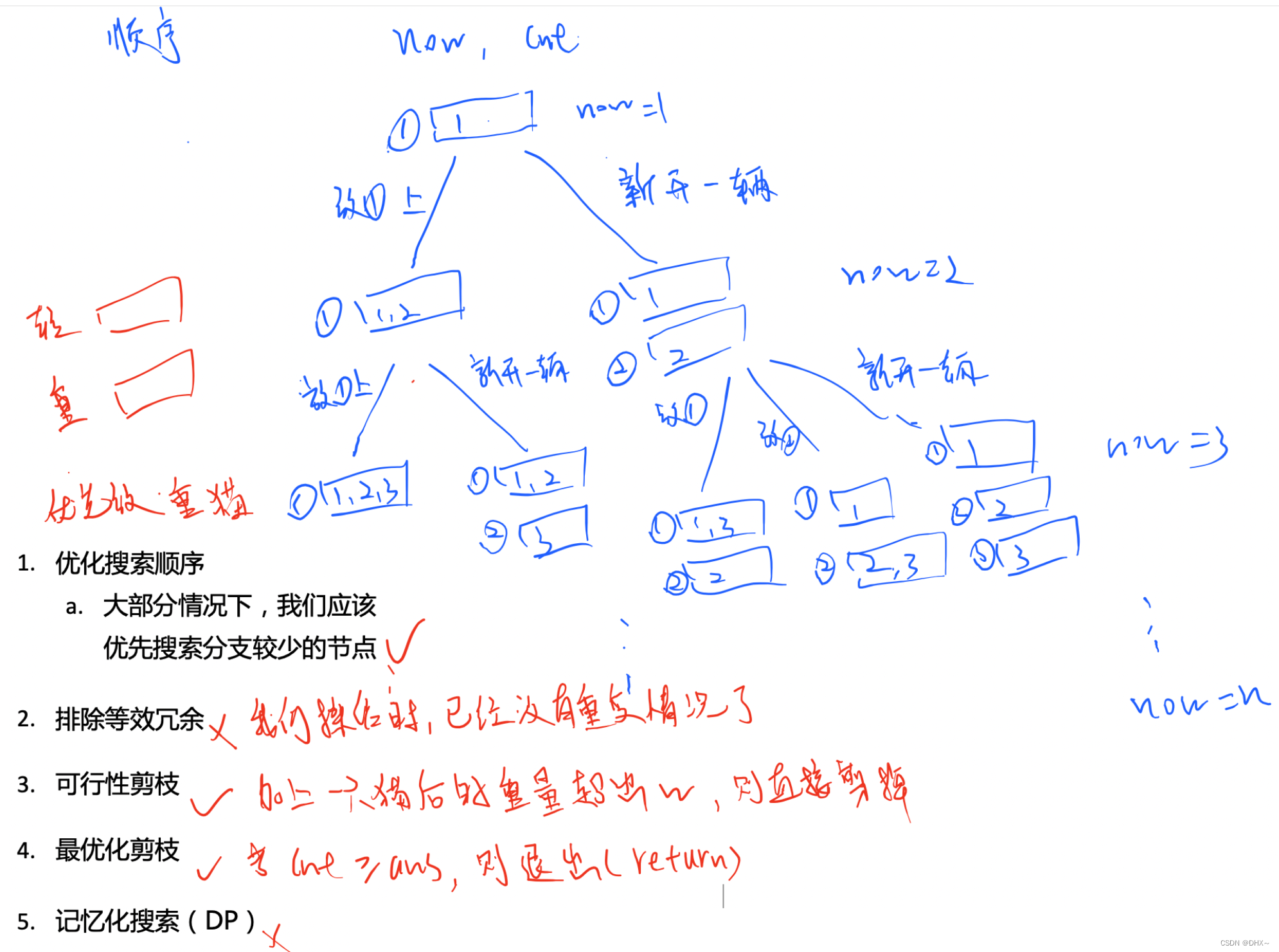

#include<iostream>
#include<algorithm>
using namespace std;
const int N=20;
int sum[N];//用来表示 在用过的缆车中 小猫的总重量
int cat[N];
int n,w;
int ans=N;//全局变量 用来找最小值
int cmp(int x,int y)
{
return x>y;
}
void dfs(int u,int num)
{
// 最优性剪枝
if(num>=ans) return ;
if(u==n+1) ans=num;
for(int i=1;i<=num;i++)
{
if(sum[i]+cat[u]<=w)// 可行性剪枝
{
sum[i]+=cat[u];
dfs(u+1,num);
sum[i]-=cat[u];// 恢复现场
}
}
//若在所使用的车辆中没有办法装载这只小猫 则重开一辆 若没有就会走到下面 然后在dfs
sum[num+1]=cat[u];
dfs(u+1,num+1);
sum[num+1]-=cat[u];//或者 sum[num+1]=0 都一样的意思 恢复现场
}
int main()
{
cin>>n>>w;
for(int i=1;i<=n;i++)cin>>cat[i];
//优化搜索顺序 从大到小排 可以减少搜索分支
sort(cat+1,cat+1+n,cmp);
dfs(1,1);
cout<<ans<<endl;
return 0;
}数独
数独 是一种传统益智游戏,你需要把一个 9×9 的数独补充完整,使得数独中每行、每列、每个 3×3 的九宫格内数字 1∼9 均恰好出现一次。
请编写一个程序填写数独。
输入格式
输入包含多组测试用例。
每个测试用例占一行,包含 81 个字符,代表数独的 81 个格内数据(顺序总体由上到下,同行由左到右)。
每个字符都是一个数字(1−9)或一个 .(表示尚未填充)。
您可以假设输入中的每个谜题都只有一个解决方案。
文件结尾处为包含单词 end 的单行,表示输入结束。
输出格式
每个测试用例,输出一行数据,代表填充完全后的数独。
输入样例:
4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......
......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3.
end
输出样例:
417369825632158947958724316825437169791586432346912758289643571573291684164875293
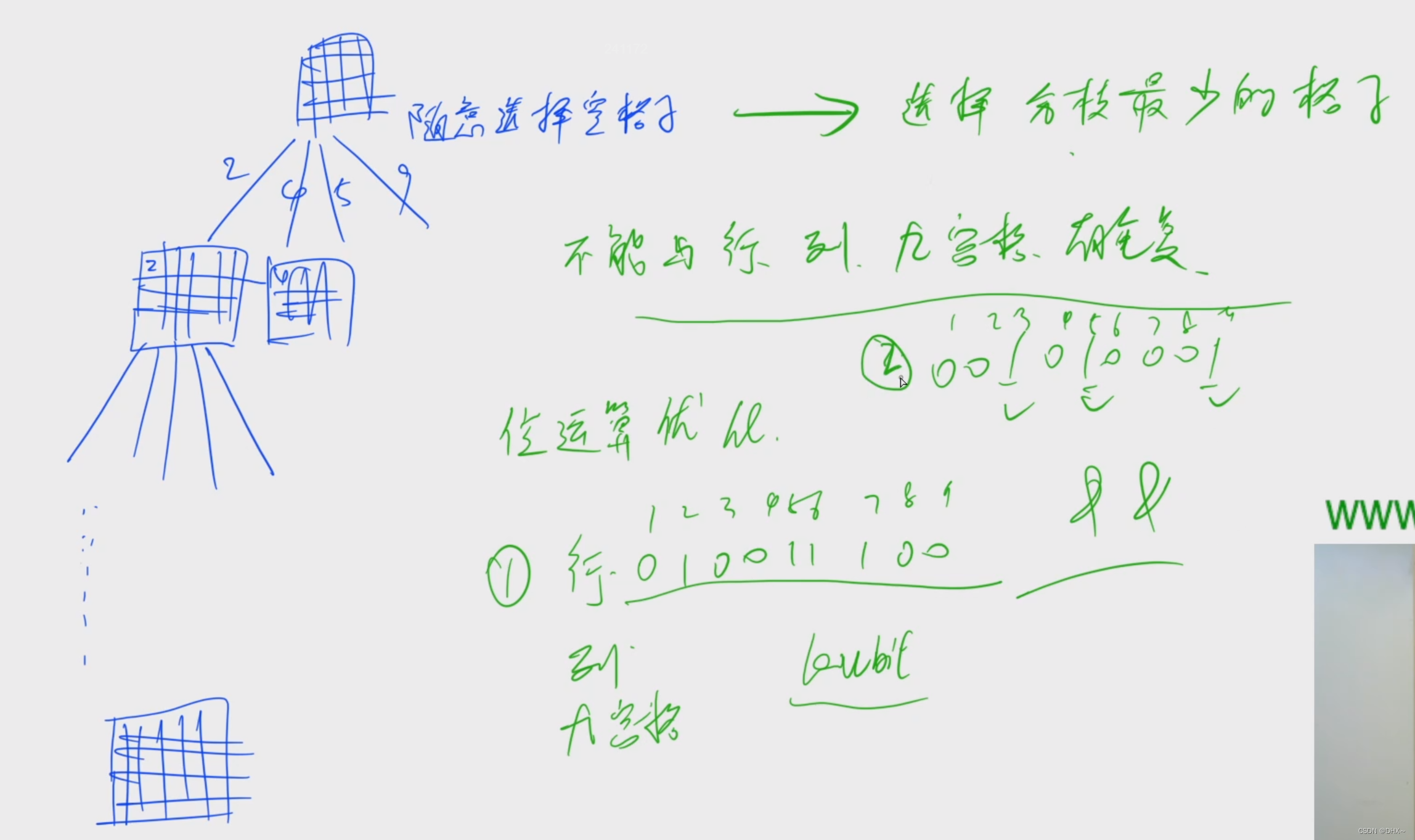
416837529982465371735129468571298643293746185864351297647913852359682714128574936位运算
(1)求n的二进制表示第k为是几
(1)先把第k位移到最后一位 n>>k
(2)看各位是几 x&1
(n>>k)&1
#include<iostream>
using namespace std;
int main()
{
int n=57;
for(int k=5;k>=0;k--) cout<<((n>>k)&1);
return 0;
}(2) lowbit(x) 返回x的最后一位1
x=1010 lowbit(x)=10;
10001000100100 lowbit(x)=100

可以计算 x中由多少1
#include<iostream>
using namespace std;
int lowbit(int x)
{
return x&-x;
}
int main()
{
int n;cin>>n;
while(n--)
{
int x;cin>>x;
int sum=0;
while(x)
{
x-=lowbit(x);
sum++;
}
cout<<sum<<" ";
}
} 
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=9,M=1<<N;//M右移9 M=(1000000000)2=512;
//one[M] 0~511 中对应的二进制中由多少个1,mp[M] 对应的是在M的状态下 那一排或哪一列可以改变 快速反应
int one[M],mp[M];
int col[N],row[N],cell[3][3];//列 行 3*3 九宫格
char str[100];//存储
void unit()
{
//初始化 所有位置都可以填数 都为1 的状态
//col[0]=row[0]=511=111111111
//col[1]=row[1]=511=111111111
for(int i=0;i<N;i++) col[i]=row[i]=(1<<N)-1;
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
{
cell[i][j]=(1<<N)-1;//每个3 * 3的小方格也用二进制来优化(刚开始也都为1)
}
}
// 在(x, y)的位置上(is_set)<是/否>填t的操作
void draw(int x,int y,int t,bool is_set)
{
if(is_set) str[x*N+y]=t+'1';//如果填数的话, 将该数转换为字符形式填入字符串中对应的位置
else str[x*N+y]='.';// 否则说明字符串该位置上填的是'.';
int v=1<<t;// 找到该数对应二进制之后的位置的数
if(!is_set) //恢复现场
{
row[x]+=v;
col[y]+=v;
cell[x/3][y/3]+=v;
}
else
{
row[x]-=v;//在这个原数对应的行减去该数的二进制数
col[y]-=v;// 在这个原数对应的列减去该数的二进制数
cell[x/3][y/3]-=v;// 在这个原数对应的小方格减去该数的二进制数
}
}
int get(int x,int y)
{
return row[x] & col[y] & cell[x/3][y/3];
}
int lowbit(int x)
{
return x & -x;
}
bool dfs(int cnt)
{
if(!cnt) return true;// 知道没有位置能填数就结束搜索
int minv=10;// 记录当前最少枚举方案
int x,y;// x, y记录枚举方案最少的位置的x, y
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
{
if(str[i*N+j]=='.')// 该位置对应的字符串位置上为'.', 才说明能填数
{
int state=get(i,j);// 找到该位置上能填的数的状态
if(one[state]<minv)// 只有当当前位置的方案少于当前最少方案才有搜索的必要
{
x=i,y=j;
minv=one[state];
}
}
}
}
int state=get(x,y);// 找到最少枚举方案对应的位置(一个格子)的能填的数的状态
for(int i=state;i;i-=lowbit(i))// 枚举该位置上能填的数,用lowbit操作
{
int t=mp[lowbit(i)];// 找到该位置上能填的数
draw(x,y,t,true);// 填数
if(dfs(cnt-1)) return true;// 继续搜索
else draw(x,y,t,false);// 恢复
}
return false;
}
int main()
{
//mp[1]=1,mp[(10)2]=mp[2]=2,mp[(100)2]=mp[4]=3,mp[(1000)2]=mp[8]=4
//预处理 可以快速得到 哪一排或者哪一列 哪个位置 有1 可以动
for(int i=0;i<N;i++) mp[1<<i]=i;
//预处理one[i]
for(int i=0;i<M;i++)
{
// i的表示 0~511->0~111111111 9位数9个状态
for(int j=0;j<N;j++)
{
//看i 的每一位是否是1 是则加上
one[i]+=(i>>j)&1;
}
}
while(cin>>str)//多组输入 字符串类型
{
if(str[0]=='e') break;
unit();
int cnt=0;//记录有几个空格需要填数
// cout<<str<<endl;
for(int i=0,k=0;i<N;i++)
{
for(int j=0;j<N;j++,k++)
{
if(str[k]!='.')
{
int t=str[k]-'1';//str[k]是 1~9 将其转化为int型的 0~8 9位数9个状态
draw(i,j,t,true);
}
else cnt++;
}
}
dfs(cnt);
cout<<str<<endl;
}
return 0;
}