思维导图

基础知识
二维随机变量
我们研究一个多维的东西,往往先从较低的维度比如说二维作为主要的研究对象,一个是因为维度低会比较简单,易于理解;另一个则是考试中低维的问题往往更加常见
定义与分布函数
定义上其实很简单,其实就是之前的一维随机变量变两个,然后用向量来表示,比如
(X,Y)
当然和一维的情况类似,二维我们也是借助分布函数来研究。
分布函数
定义:设(X,Y)是二维随机变量,对于任意实数x,y,有二元函数
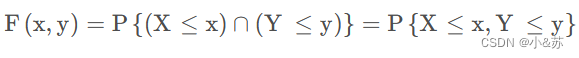 该函数就是二维随机变量(X,Y)的分布函数,这种分布函数还有另外一个名字:X和Y的联合分布函数
该函数就是二维随机变量(X,Y)的分布函数,这种分布函数还有另外一个名字:X和Y的联合分布函数
分布函数的基本性质
1.不减,其实就和一维的一样,类似于多元里的求偏导,我们固定一个维度,比如y或x,然后另外一个维度就是一个不减的情况。
2.范围是[0,1]
3.两个维度上的左右连续
4.对于任意的(x1,y1),(x2,y2),x1<x2,y1<y2。则有下列不等式
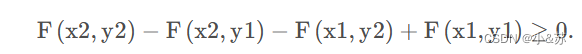
离散型
类比一维的离散型,其实还是有限对或者可列无限多对情况。
然后和一维的一样,也有分布律,在本节中主要是联合分布律。
联合分布律
其实就是求P{X=i,Y=j},结合分布函数或许比较好理解。
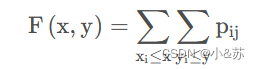
连续型
回想一维的,其实从概率密度到分布函数是一个积分的过程,而二维也是类似,不过用到了重积分
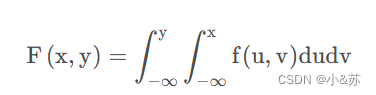
和上面的联合分布律类似,概率密度也有联合概率密度。
至于它的基本性质类比一维。
联合概率密度
基本性质:
1.非负
2.规范性
3.几何性质
4.点的连续性
边缘分布
前面的
F(X,Y)
是联合分布函数,当我们只选取其中的一个变量的时候,得到的函数如
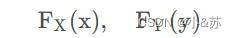
就叫做边缘分布函数,由于联合分布的其中一个性质
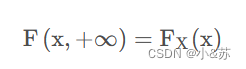
FY(y)同理
我们还是分离散型和连续型两类来考虑边缘分布函数。
离散型
离散型分布对应的边缘分布律,我们通过前面的公式可以得到
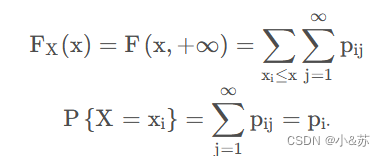
离散型二维随机变量(X,Y)关于X的边缘分布函数和边缘分布律,Y同理。
连续型
结合一维的情况,离散型从分布律到分布函数是用加和,而连续型从概率密度到分布函数用积分,边缘分布也是如此。
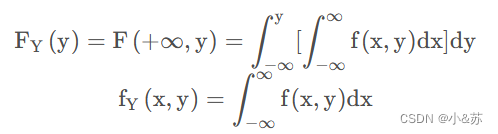
公式的理解
其实很好理解,当我们需要求边缘的时候,肯定需要忽略其他因素,这时就是只考虑边缘因素将联合概率重分配,或者划分,就可以得到边缘分布的情况。
条件分布
我们联系第一章的条件概率
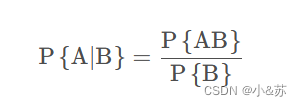
再看下面的条件概率公式
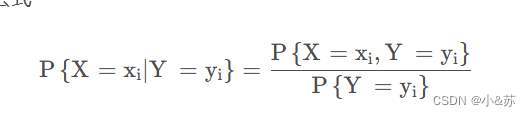 分子是联合概率,分母是边缘概率,即条件。
分子是联合概率,分母是边缘概率,即条件。
注意分母不能为0!!!
离散型
对于离散,我们只要思考两个东西:分布函数和分布律。
而分布函数其实就是分布律的加和,所以我们只研究分布律即可。
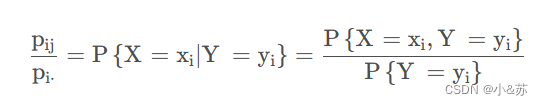
这个其实就是条件分布律。
连续型
离散研究分布律,连续就看概率密度
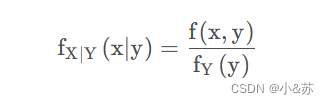
这就是条件概率密度。
相互独立的随机变量
这一部分的知识点其实也是很简单的,就是一个二维随机变量的两个分量在几何上属于绝对垂直的i情况,即互无影响,互相独立,
对于独立事件,有
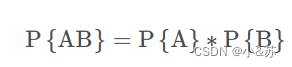
而在本节中,变成了
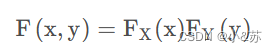
即联合分布维两个边缘分布的乘积,此时X和Y相互独立。
两个随机变量的函数的分布
**注意:**本节内容只涉及
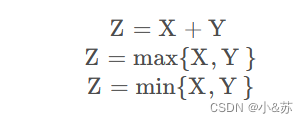 除此之外,以下都是关于连续型,而离散型只需要我们把分布律列出来即可。
除此之外,以下都是关于连续型,而离散型只需要我们把分布律列出来即可。
Z=X+Y
z=x+y这个条件,我们可以做出替换,比如,x=z-y,或者y=z-x,然后得到下列关于z的概率密度
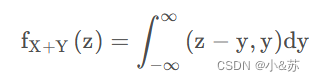
通过积分后就可以得到只与z相关的概率密度函数。
如果X和Y独立,那么有
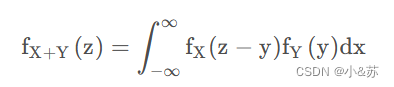
这种公式又称为卷积公式。
小定理
有限个相互独立的正态随机变量的线性组合仍然服从正态分布。
Z = max{X, Y} 和 Z= min{X,Y}
手写笔记




课后习题

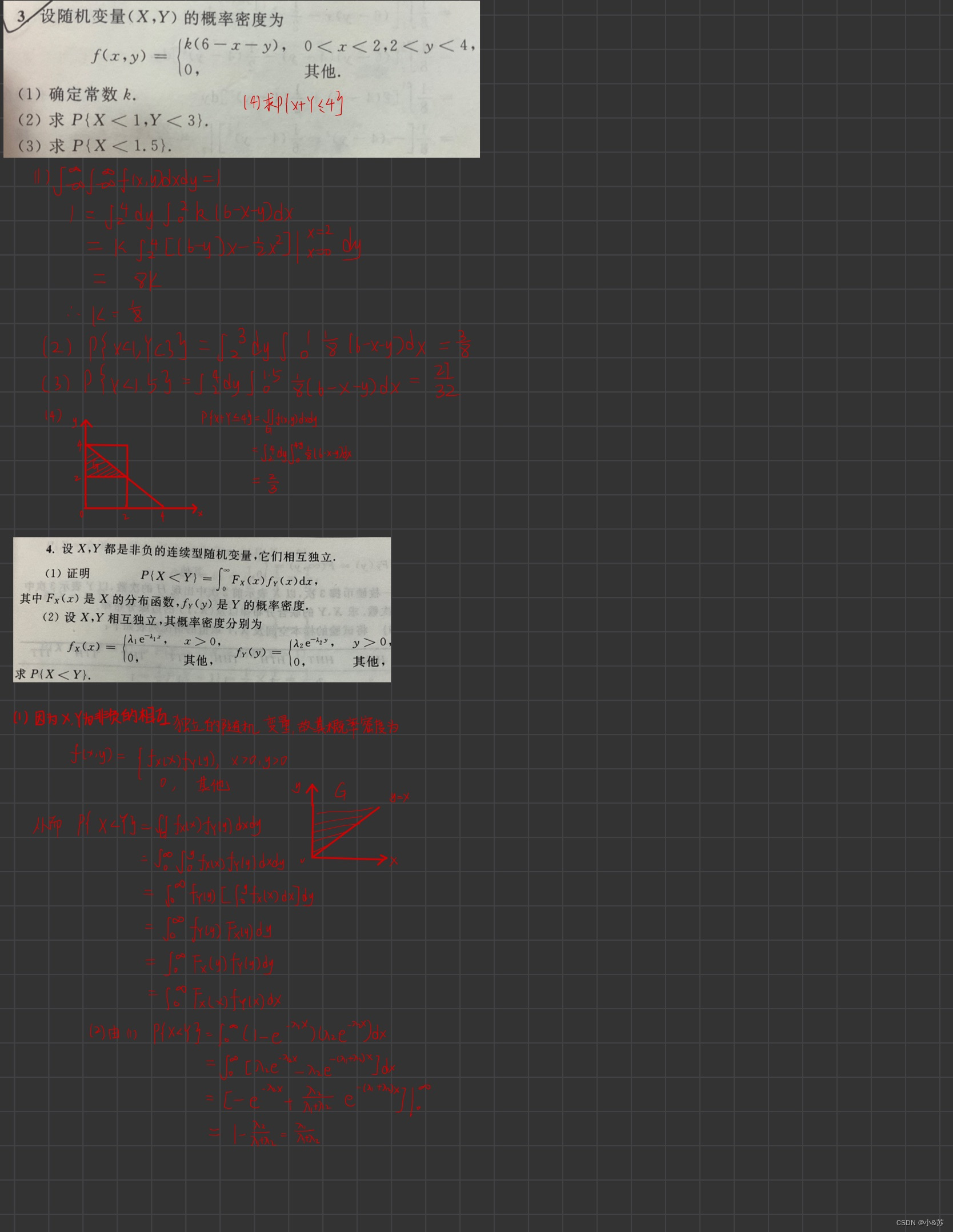
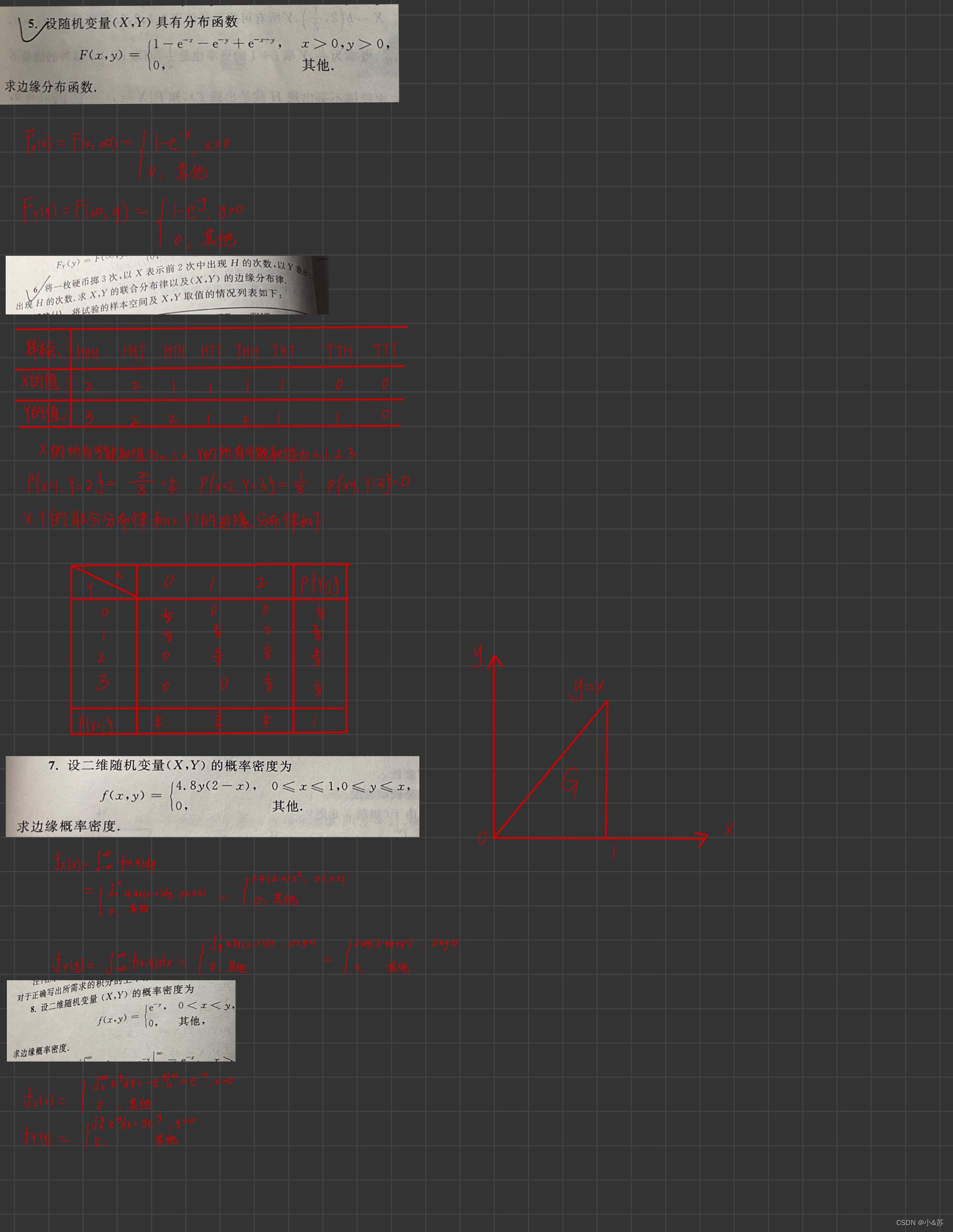
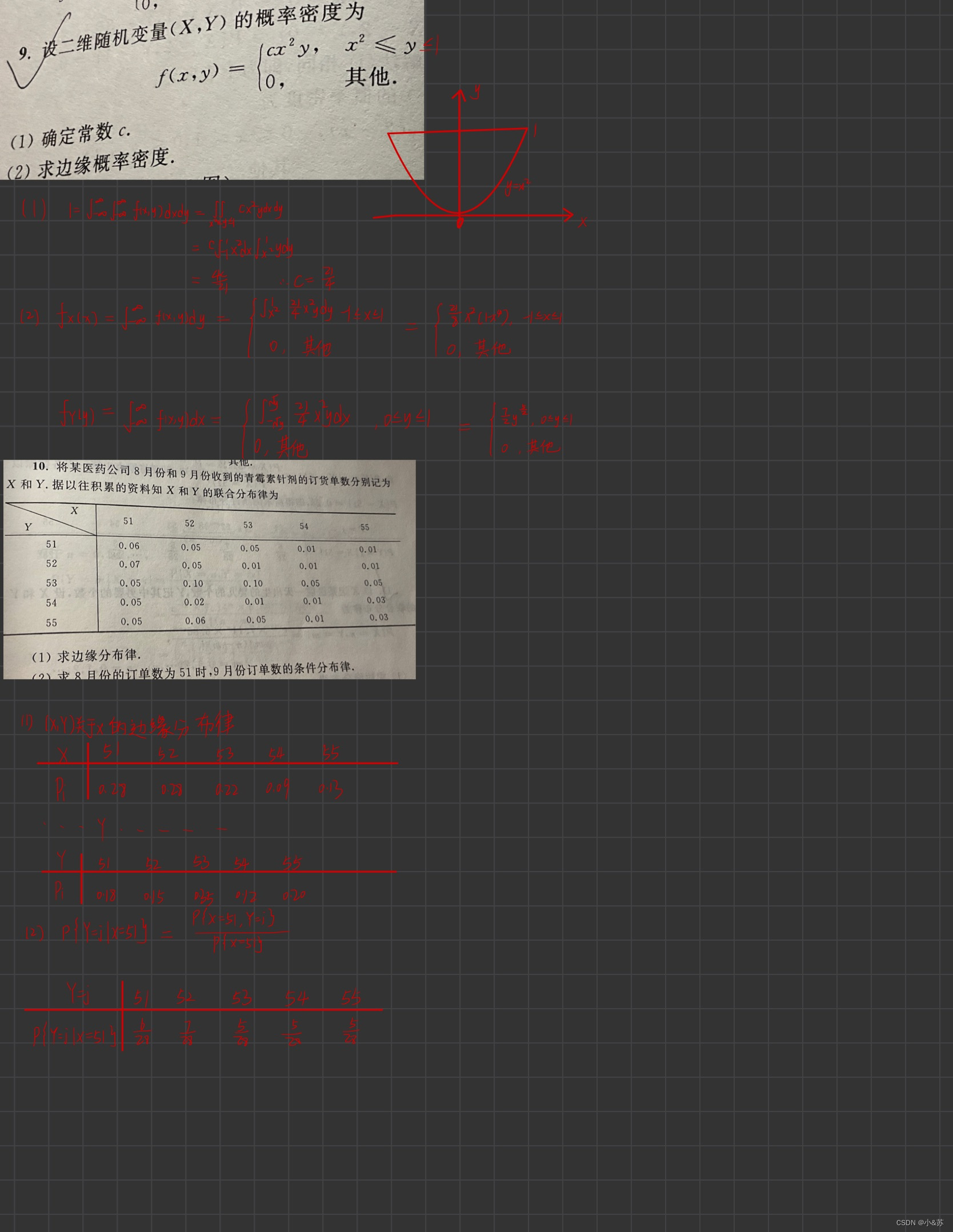
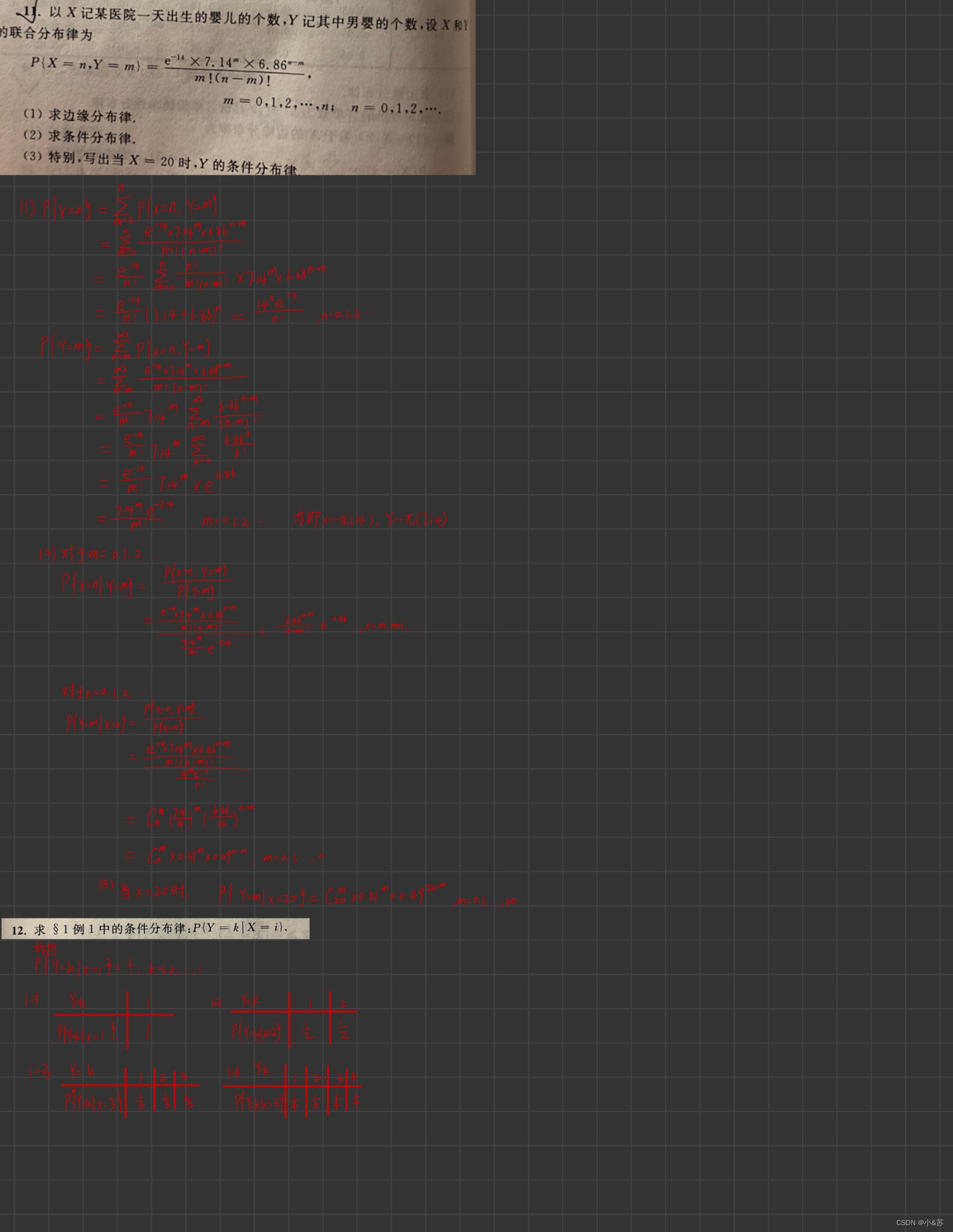

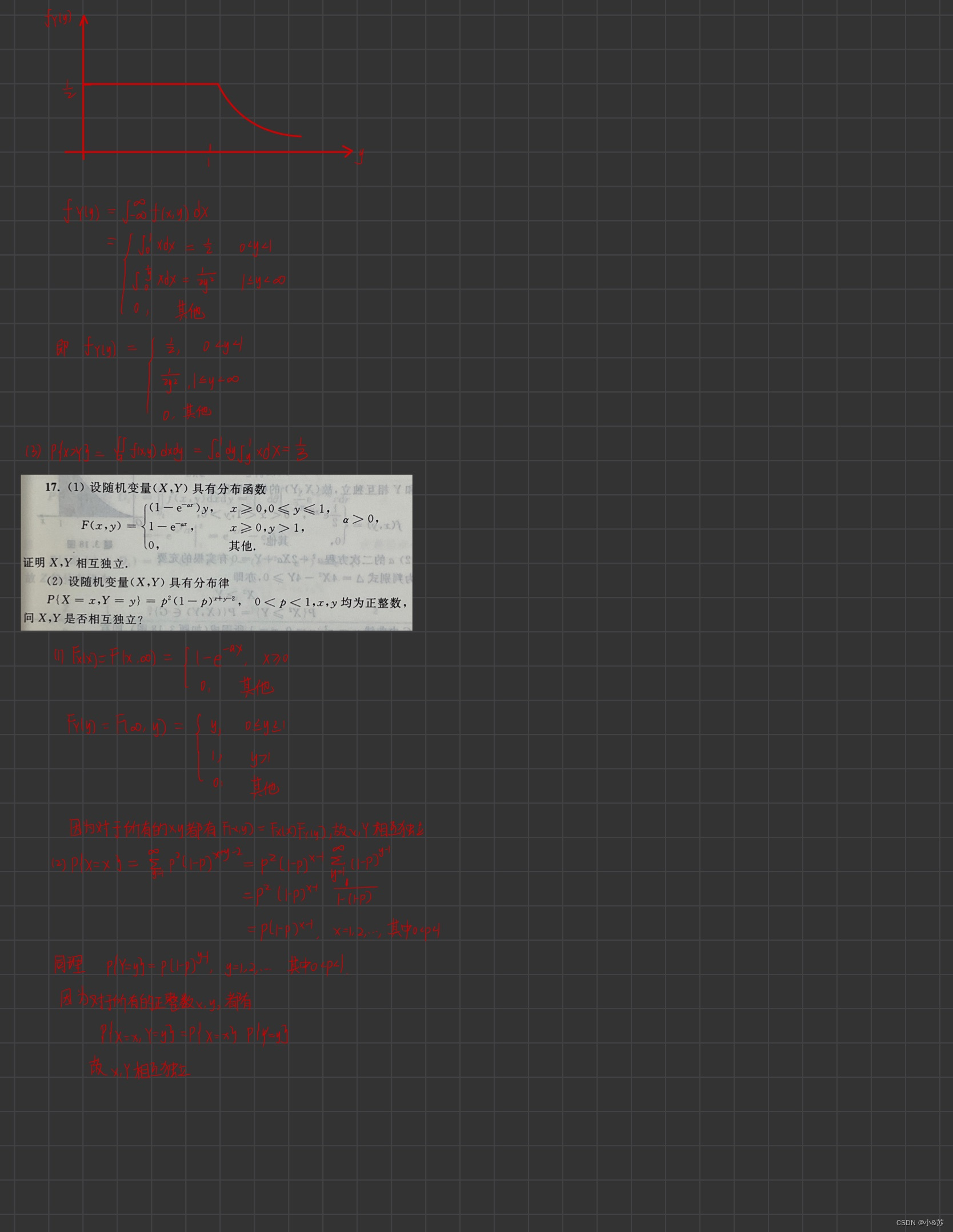
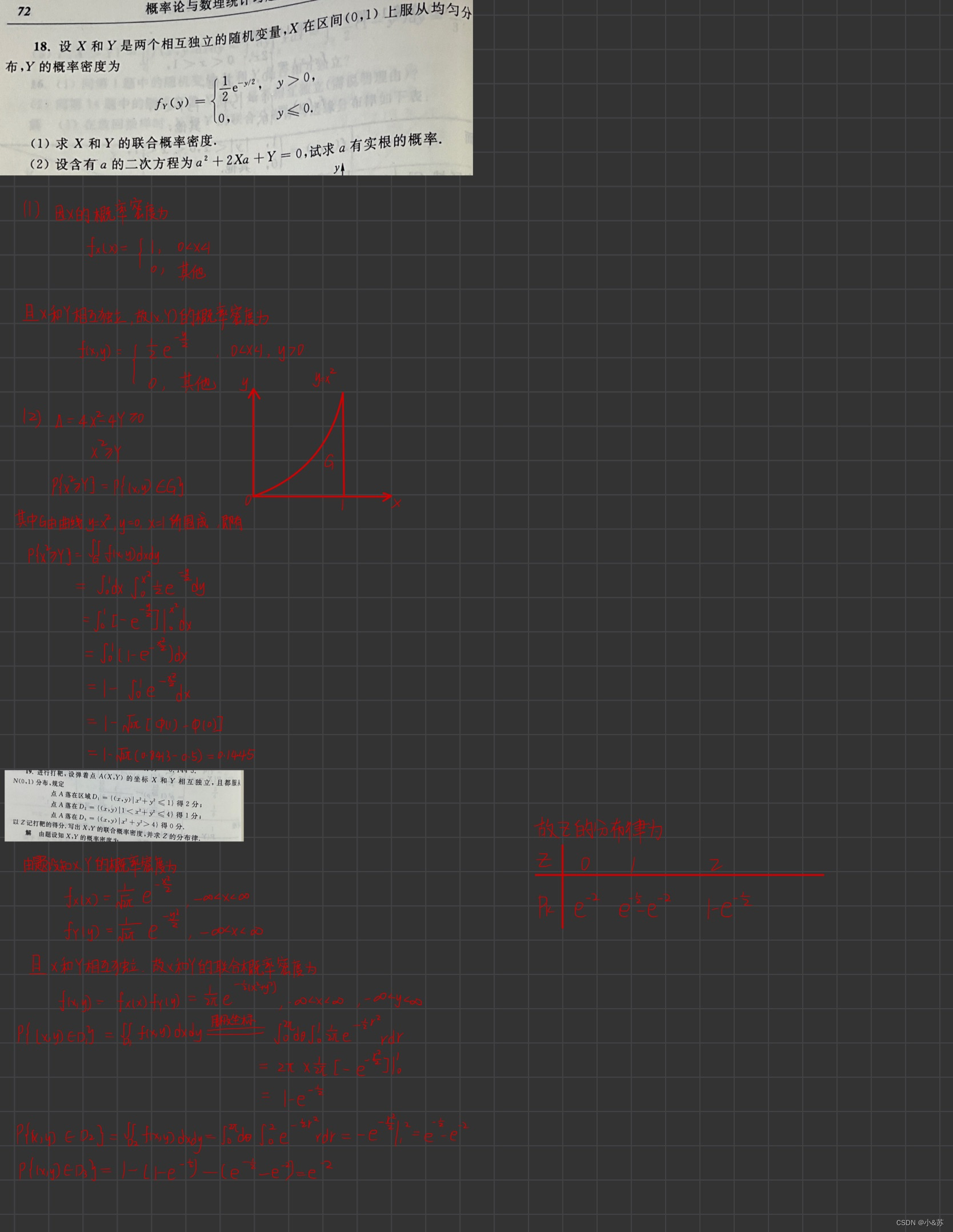
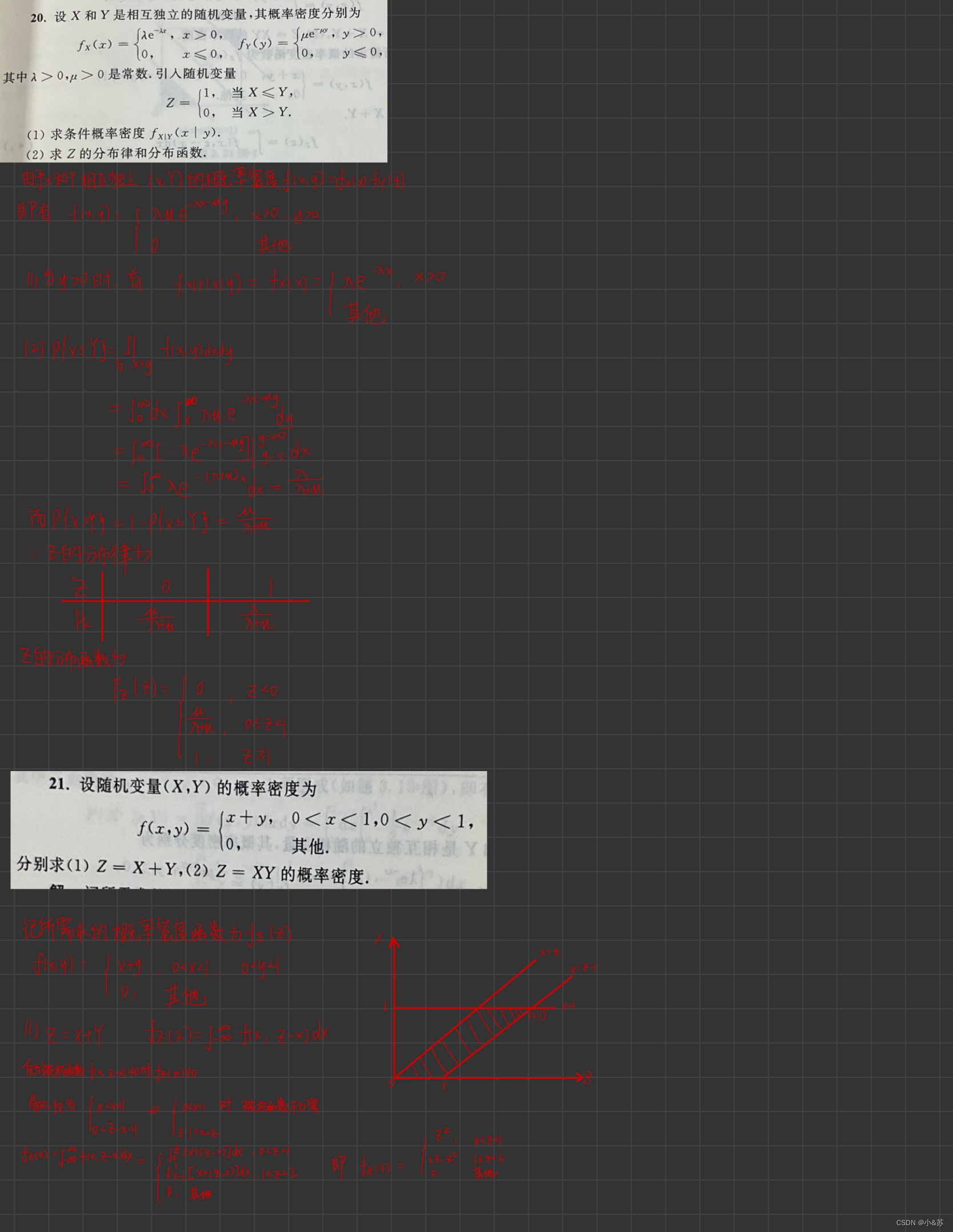
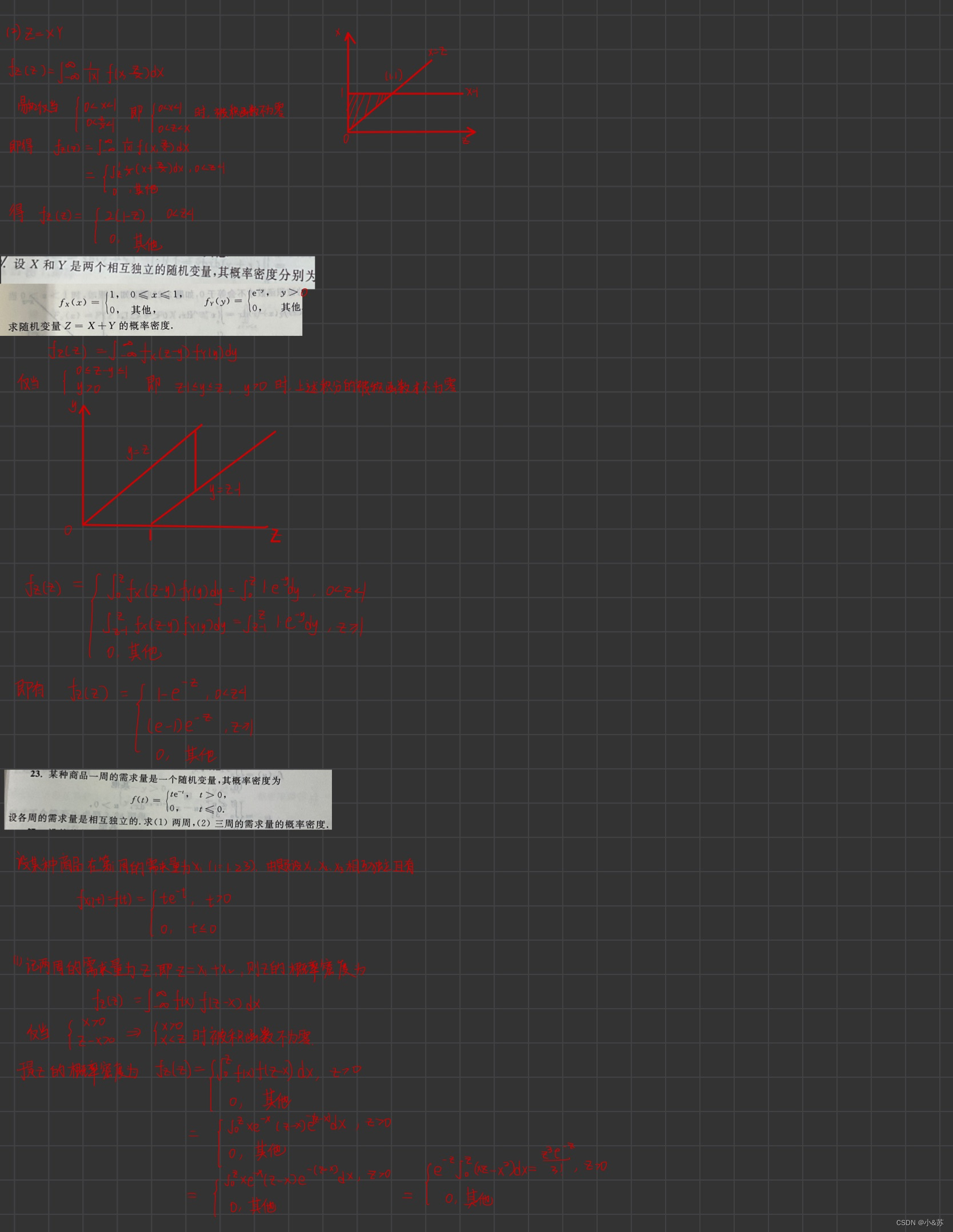
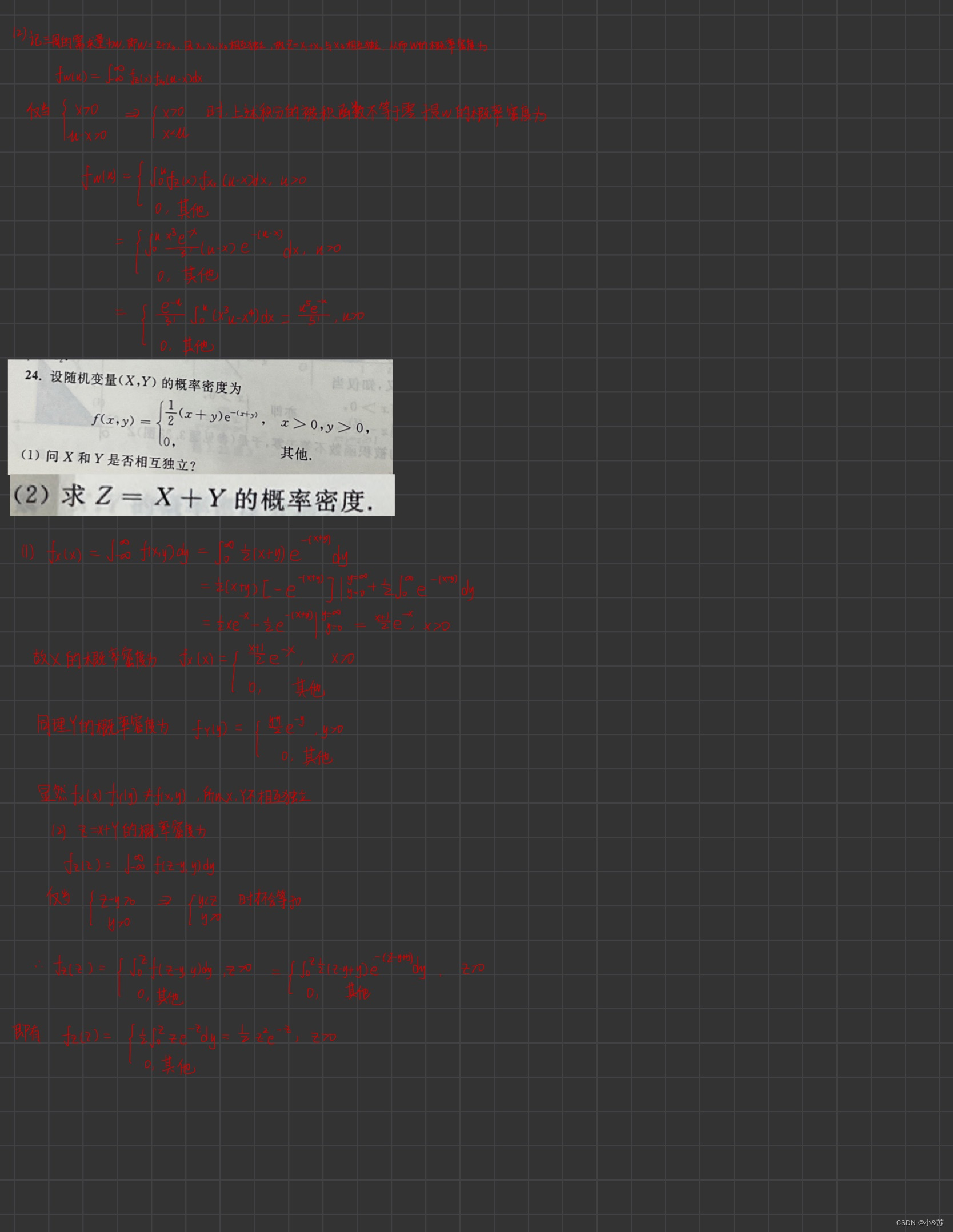


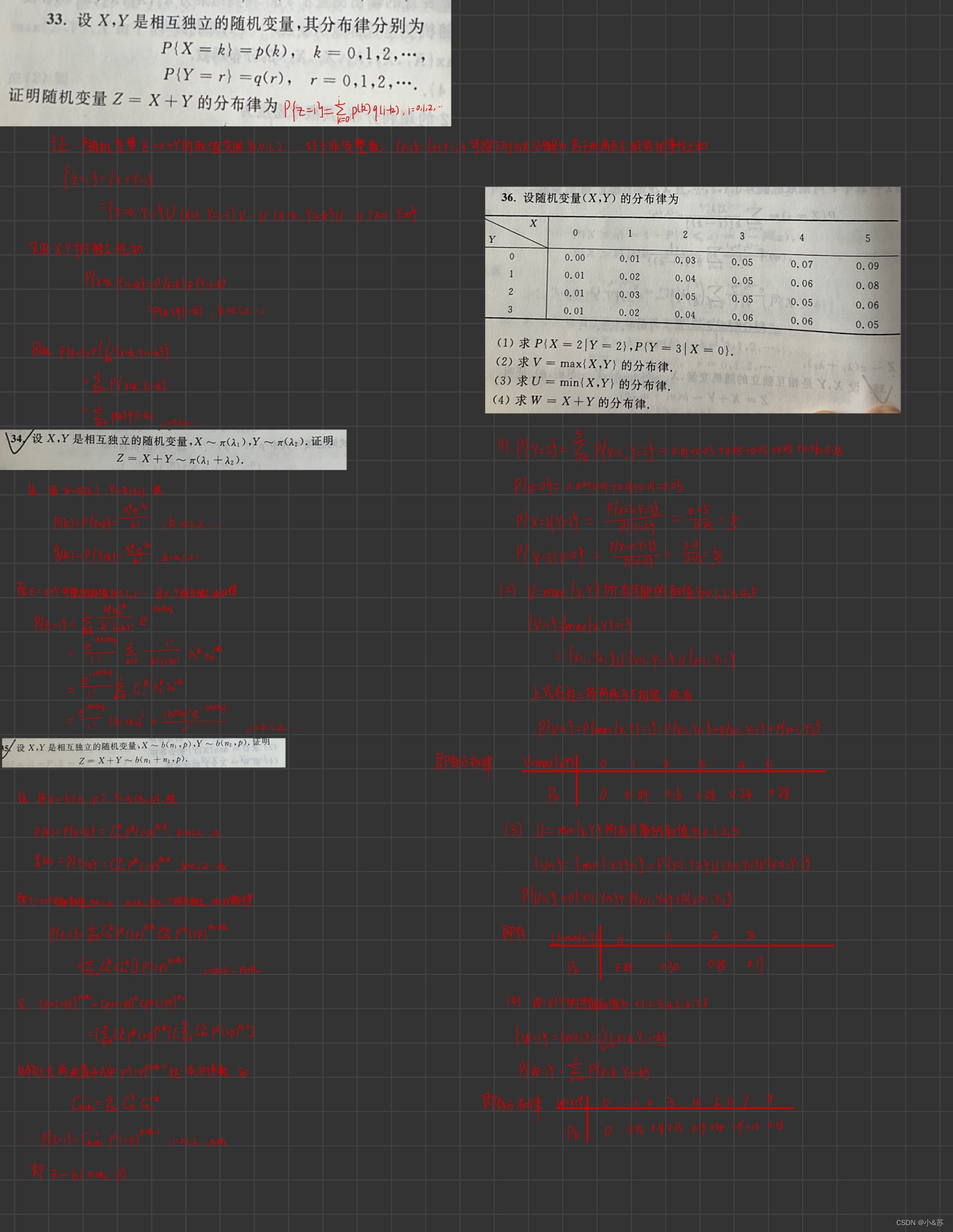





![[附源码]java毕业设计基于的楼盘销售管理系统论文2022](https://img-blog.csdnimg.cn/0b6bd4677d5a40dc8aa9674e198c5845.png)