前言
量子计算机不仅有望在某些重要任务上超越经典计算机,而且还能保护计算的隐私。例如,盲量子计算协议支持安全委托量子计算,其中客户端可以保护其数据和算法的隐私,不受分配来运行计算的量子服务器的影响。然而,这种安全性带来了实际的限制,即客户端和服务器必须在每一步计算之后进行通信。一种实用的替代方案是同态加密,它不需要任何交互,同时为各种计算提供量子增强的数据安全性。在这个场景中,服务器指定要执行的计算,客户机只提供输入数据,从而支持安全的非交互式计算。本文将展示具有单个量子比特的幺正变换的同态加密量子计算,以及使用单光子态和非双折射集成光学的多量子比特量子行走计算。客户端在光子偏振状态下加密它们的输入,而服务器使用路径自由度执行计算。
背景
安全委托计算一直是经典计算界和量子计算界长期以来的研究目标。其目的是为客户端(Alice)提供对远程计算资源(Bob)的访问,同时保护Alice的数据和Bob的算法的隐私。在他2009年的开创性论文中,Gentry描述了第一个用于经典计算的计算安全的、完全同态的加密方案。这里,“计算安全”意味着协议的隐私保证是基于对对手计算能力的假设;“完全”意味着任何计算都是可能的。盲量子计算也在2009年被引入,该协议解决了一种不同的情况,在这种情况下,数据和算法都属于Alice, Alice想要使用Bob的远程计算资源而不泄露它们。盲量子计算具有信息理论上安全的优点(即,它不依赖于对对手技术能力的假设),并且允许在计算过程中Alice和Bob之间进行多轮通信。它的效率受到交互需求的限制:Alice和Bob必须在计算的每一步之后在经典信道内交换信息。量子同态加密中,量子计算是在量子信息上执行的,消除了交互计算的要求并增加了通信效率,但根据一个不可行定理(如果需要完美的隐私和非指数资源开销,则完全同态加密是不可能的),必须牺牲安全性或计算能力来实现完美隐私与开销减少。
Rohde等人的提议表明,放宽对(1)通用量子计算和(2)完美隐私的要求,可以使用光子量子处理器实现新的量子同态加密方法。光子具有多个自由度来编码量子信息,从而实现同态加密量子行走。尽管量子行走只提供通用量子计算的子集,但由于其适用性,从机器学习算法到搜索算法和玻色子采样,这些计算引起了人们的极大兴趣。关于安全性,还表明,在任何实际的加密应用程序中,只要攻击者可能获得的最大信息量足够小,就不需要完美的隐私。请注意,正在讨论的是量子加密量子计算的任务,因此不应将其安全性与经典计算的现有经典技术进行比较。
环境说明
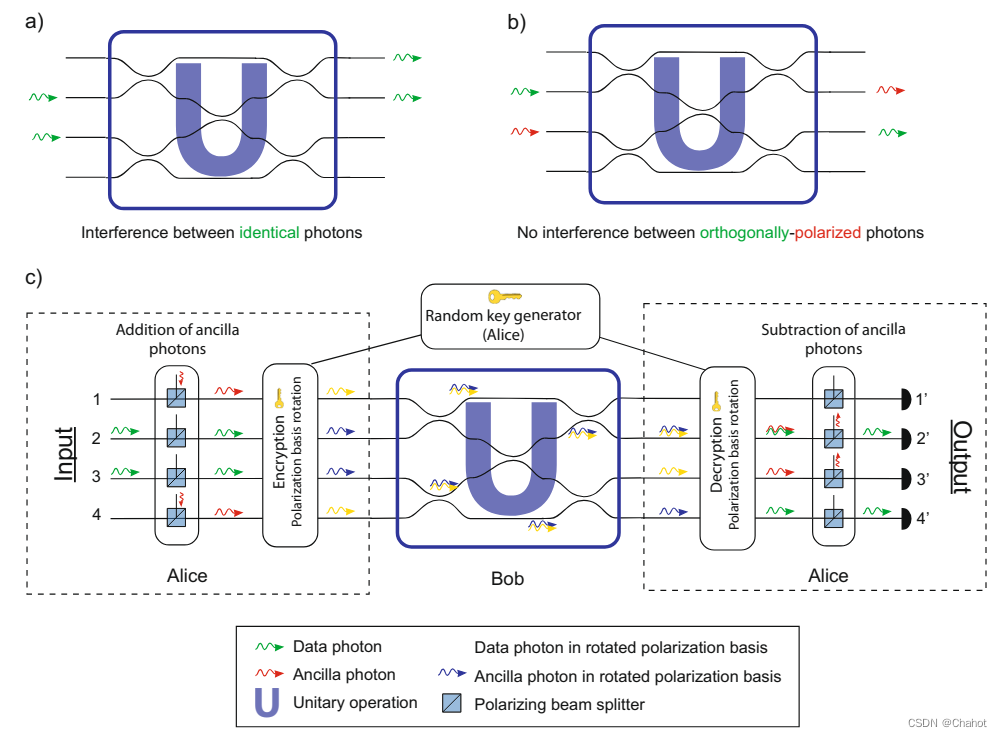
在本实验中,我们使用单光子量子比特输入状态和集成光学服务器来实验证明由Rohde等人描述的量子同态协议。量子行走输入通常是分布在m个空间模式上的n个光子,每个模式中不超过一个光子。协议通过使用光子的偏振来编码Alice的量子行走输入,从而隐藏了这些光子的分布(利用正交偏振光子不干涉的事实)。否则,空模式会被辅助光子填充。因此,为了实现n个“游走”光子的m模量子行走,我们也输入m- n,而不是在n个模式中每个模式输入一个光子并留下剩余的m- n个在其他空模式中的“假”光子,其偏振与代表游走的n个光子正交。
假设输入状态为
∣
ψ
i
n
⟩
=
∣
1000
⟩
|\psi_{in}\rangle=|1000\rangle
∣ψin⟩=∣1000⟩,且编码模式为
∣
ψ
i
n
−
e
n
c
o
d
e
d
⟩
=
∣
H
V
V
V
⟩
|\psi_{in-encoded}\rangle=|HVVV\rangle
∣ψin−encoded⟩=∣HVVV⟩,其中H和V分别表示水平和垂直的极化。测量{H, V}基的输出光子,然后得到与传统的经典数量子行走相同的结果。这种方法的目的是对Alice的输入状态进行极化加密:在不知道Alice的输入被编码的基础的情况下,Bob可以猜测Alice的输入状态,并且成功的概率有限。为了加密这个输入态,从Poincaré球取一个均匀分布点d中选择一个极化基
∣
X
⟩
|X\rangle
∣X⟩。为了加密这个数据,Alie旋转他的量子比特(
∣
H
⟩
|H\rangle
∣H⟩to
∣
X
⟩
|X\rangle
∣X⟩or
∣
V
⟩
|V\rangle
∣V⟩to
∣
X
⊥
⟩
|X^⊥\rangle
∣X⊥⟩)。Alice将这个加密状态发送给Bob, Bob执行量子行走。Bob将输出的光子返回给Alice,她在
X
,
X
⊥
{X, X^⊥}
X,X⊥基中测量它们,得到量子行走的结果。
如果Bob试图破译Alice的加密状态,他能提取的信息量就受Holevo量的限制。Bob可以采用的一种直接攻击是随机选择一个基,在其中测量所有m个光子:事实上,这种攻击接近最优,几乎饱和了Holevo边界。在大d和m的极限下,该攻击的成功概率为
p
B
=
1
/
π
m
p_B=1/\sqrt{πm}
pB=1/πm。该协议还保证了Bob算法的隐私性。由于Alice只知道计算的输入和输出状态,她可以提取的关于Bob算法的信息量与“黑箱”函数的信息量成正比:她被允许发送的查询越多,她对函数的猜测就越准确。值得注意的是,Alice和Bob都希望对特定的输入状态执行一次特定的计算,因为随着计算重复次数的增加,他们各自的秘密的隐私被损害的概率会越来越大。不可能定理断言这种限制是不可避免的。
Poincaré球:Poincaré球是用于表示偏振光状态的一种图形工具。它可以用来可视化不同类型的偏振光,并计算偏振元件的影响。Poincaré球由亨利·庞加莱(Henri Poincaré)于1892年提出,是一种在偏振光学中常用的表示方法。这个球形图示了偏振光的各种状态,并可以用其球面和笛卡尔坐标来描述。在Poincaré球上,每个偏振状态都由唯一的点表示,该点由方位角α、椭圆度tan(ε)和偏振旋转方向(左旋或右旋)定义。垂直偏振方向位于球的两端,而水平线性偏振方向则位于球的赤道。通过旋转球体,可以表示通过各种偏振元件后的偏振状态。Poincaré球的使用可以简化偏振光学计算,并使得可视化偏振状态更加直观。
Holevo边界:Holevo边界是量子信息理论中的一个重要概念,它是由俄罗斯物理学家阿耶·霍列沃(A. S. Holevo)在1973年提出的。Holevo边界是用于限制量子信道中信息传输的最大容量的一个重要界限。Holevo边界告诉我们,在给定的量子信道中,我们最多可以传输多少量子比特的信息。具体来说,Holevo边界给出了通过量子信道传输的最大量子信息容量。这个容量是由信道的特性和信号之间的关系所决定的。
实现细节
在实验演示中,Alice使用两个自发参数下转换(SPDC)源产生四个光子,并为每个光子使用偏振器、半波片(HWP)和四分之一波片(QWP)在随机选择的偏振状态下制备它们。Alice可以创建任意偏振的输入态,保真度为(99.5±0.1)%,主要误差来源是通向芯片的单模光纤偏振补偿不完善。在准备好加密的输入状态后,Alice将光子发送给Bob, Bob执行量子行走。为了使方案有效,Bob的芯片必须对光子的路径自由度实现相同的统一,否则,结果将取决于Alice选择的密钥。虽然激光写入波导支持所有偏振的传播,但它们通常具有H和V偏振的稍微不同的折射率(Δn≈10−5),这使得实现非平凡的偏振无关路径单一化成为一项挑战。为了实现这一点,使用退火程序来制造双折射波导
Δ
<
1
0
−
6
\Delta<10^{-6}
Δ<10−6将是一个合理且可行的方案。
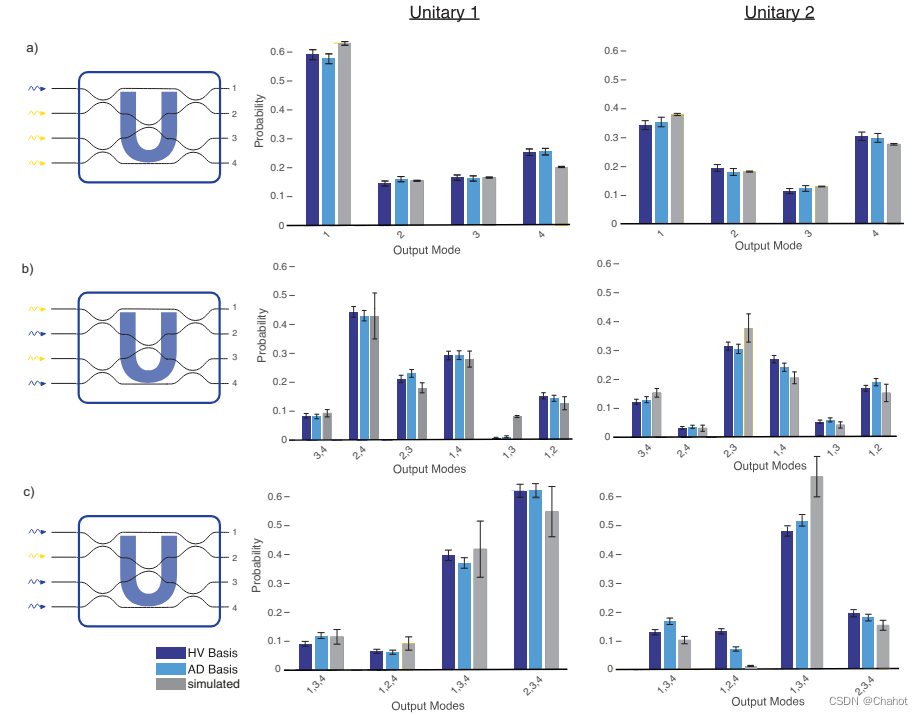
在量子行走之后,Bob将光子返回给Alice, Alice使用QWPs、HWPs、偏振分束器(PBSs)和单光子探测器以她之前选择的偏振基投射光子。为了证明同态加密量子行走的保真度,可以选择了一个由两个相互无偏极化基组成的规范集,并使用两个不同的酉进行了一个、两个和三个步行者的量子行走,每个步行者有m = 4个输入和输出。
安全性分析
对Alice明文输入状态的安全保证可以通过多种方式进行量化。她可以用四个光子产生的不同输入状态之间的迹距在汉明距离1和3下为0.81,在汉明距离2下为0.85。结果,Bob不能完全区分任何一对可能的明文。此外,她的明文字符串和Bob之间的互信息由Holevo量限定为大于1.96bits。为了实验验证Alice输入的安全性,我们实现了上面描述的攻击:Bob在随机选择的基础上测量Alice的所有四个光子(这里我们选择
∣
H
⟩
|H\rangle
∣H⟩)。Alice加密她的明文输入状态(这里我们使用
∣
1111
⟩
=
∣
H
H
H
H
⟩
|1111\rangle=|HHHH\rangle
∣1111⟩=∣HHHH⟩)通过在d = 2,3,4,6,12个不同的线极化基(密钥)之间进行选择。Bob猜测Alice明文输入状态的概率可以从Bob用偏振测量的四重重合检测的分数中确定
∣
H
H
H
H
⟩
|HHHH\rangle
∣HHHH⟩。在m = 4和d = 2的情况下,Bob有50%的机会猜出正确的极化基。随着基数的增加,Bob确定输入状态的概率逐渐接近p = 0.27。Alice输入状态的隐私性随着模式数m和密钥数d的增加而增加:下图显示了这种依赖关系。值得注意的是,由于集成光学的快速发展,目前的技术已经可以使用高质量的相位延迟器实现几乎任意大的d,并且m可以达到几十个量级。
我们已经展示了单光子变换和多达三个游走量子的量子游走的同态加密量子计算。我们的光子系统的特殊设计功能使我们能够加密爱丽丝的偏振明文输入状态,同时使用路径自由度进行计算。Alice明文输入的安全性必然受到所使用的模式数量的限制,也就是说,受到可用光子数量的限制——然而,光子源技术的持续进步将使将来使用更多模式的类似演示成为可能。如前所述,在此协议中,计算只能尝试一次,因为每次连续尝试都会降低双方的安全性;要使这项技术成为现实,我们需要在量子纠错方面取得进展,以增加在存在损耗的情况下成功操作的可能性。进一步的改进可以通过在两个以上能级的不同光子自由度中进行加密来实现。例如,轨道角动量原则上使任意高维编码成为可能,并且这种状态在光纤中的传输已经得到证实。使用a级自由度进行编码,而不是极化,可以将隐藏信息的数量从
l
o
g
2
(
m
)
log_2(m)
log2(m)缩放到
[
m
l
o
g
2
(
a
/
m
)
+
m
l
o
g
(
2
)
]
−
1
[mlog_2(a/m)+mlog(2)]^{-1}
[mlog2(a/m)+mlog(2)]−1。
数学支持
Holevo信息边界
为了分析Bob可以从Alice状态的单个副本中获得的信息量,可以如下计算Holevo量:
X
(
m
)
=
−
T
r
(
ρ
l
o
g
2
ρ
)
+
1
2
m
∑
i
=
0
2
m
−
1
T
r
(
ρ
i
l
o
g
2
ρ
i
)
X(m)=-Tr(ρlog_2ρ)+\frac{1}{2^m}\sum_{i=0}^{2^m-1}Tr(ρ_ilog_2ρ_i)
X(m)=−Tr(ρlog2ρ)+2m1i=0∑2m−1Tr(ρilog2ρi)
上式中,当i的第j位为0时,有
ρ
=
1
2
m
∑
i
=
1
2
m
ρ
i
ρ=\frac{1}{2^m}\sum_{i=1}^{2^m}ρ_i
ρ=2m1∑i=12mρi且
ρ
i
=
∑
k
=
0
d
−
1
⊗
R
k
π
d
∣
P
i
j
⟩
×
⟨
P
i
j
∣
R
(
−
k
π
d
)
,
∣
P
i
j
⟩
=
∣
H
⟩
ρ_i=\sum_{k=0}^{d-1}\otimes R\frac{kπ}{d}|P_{ij}\rangle\times\langle P_{ij}|R(-\frac{kπ}{d}), |P_{ij}\rangle=|H\rangle
ρi=∑k=0d−1⊗Rdkπ∣Pij⟩×⟨Pij∣R(−dkπ),∣Pij⟩=∣H⟩,否则
∣
P
i
j
⟩
=
∣
V
⟩
|P_{ij}\rangle=|V\rangle
∣Pij⟩=∣V⟩。如果m=4和12,则
X
(
4
)
=
1.9694
X(4)=1.9694
X(4)=1.9694。注意,对于椭圆偏振编码,Holevo信息减半,但m的缩放保持不变。
Bob的攻击试图概率
Bob推断出正确状态的概率公式如下:(用空间模数m和可能极化基数d表示。)
p
=
1
d
∑
j
=
0
d
−
1
c
o
s
2
m
j
π
d
p=\frac{1}{d}\sum_{j=0}^{d-1}cos^{2m}\frac{j\pi}{d}
p=d1j=0∑d−1cos2mdjπ
测量误差
下转换光源的主要缺点是其发射是概率性的。因为在每个晶体中同时产生一对晶体的概率,等于在其中一个晶体中恰好产生两对晶体的概率。由于们通过极化来区分两个光源的对,进而避免了这个问题。对于输入态,其中一个光子的偏振与其他三个光子的偏振正交,输入偏振可以设置为
∣
H
H
⟩
|HH\rangle
∣HH⟩或
∣
V
V
⟩
|VV\rangle
∣VV⟩为源1,根据需要,
∣
H
V
⟩
|HV\rangle
∣HV⟩表示源2:那么爱丽丝最后的偏振测量将会把想要获得的事件与一个晶体产生全部四个光子的事件区分开来。我们也可以处理输入态有两个
∣
H
⟩
|H\rangle
∣H⟩光子和两个
∣
V
⟩
|V\rangle
∣V⟩光子通过源1和源2产生
∣
H
H
⟩
|HH\rangle
∣HH⟩和
∣
V
V
⟩
|VV\rangle
∣VV⟩,并根据需要将输入通道重新连接到芯片。输入态双对发射
∣
V
V
V
V
⟩
|VVVV\rangle
∣VVVV⟩和
∣
H
H
H
H
⟩
|HHHH\rangle
∣HHHH⟩不能用这种方式处理,但是这些状态对于量子行走来说并不重要。
抑制了双对发射的误差后,我们现在必须考虑三对发射。这些事件贡献的噪声与源的每脉冲发射概率相同,为0.14%。为了量化光子的光谱可分辨性,我们测量了信号源1的所有四种信号和闲散子组合与信号源2的信号和闲散子组合的Hong-Ou-Mandel干涉可见性。在减去统计上期望的高阶噪声后,我们测量的能见度为0.88±0.05(弱不消除高阶噪声则为0.77±0.05)。这是主要的贡献误差,减少了随机漫步中与模拟输出分布的重叠,并且它解释了随着光子数量的增加而降低保真度的原因。如果假设泊松误差适用于所有的单光子探测率,所以对于N次探测,我们假设误差为
ϵ
=
N
\epsilon=\sqrt{N}
ϵ=N。重建的酉波的误差是从强度测量的误差中传播出来的,而强度测量的误差又被用来推断振幅和相位。在这里,我们能够将推断的传输幅度和相位的误差分别限制在1%和50 mrad。各种输出可能性的误差条大小的差异源于一元的性质:相位误差可以导致某些输出概率的巨大变化,而对其他输出概率几乎没有任何影响。
小结
正如我们在这里所展示的,尽管通用计算的完美安全性(没有指数级的资源开销)是被禁止的,但是放宽这些条件可以启用有趣的应用程序。确定计算的安全性、性能和通用性的理想组合仍然是一个活跃的研究主题。