目录
桶排序
图示
伪代码
时间复杂度
基数排序
多关键字排序
代码(C语言)
次位优先
主位优先
桶排序
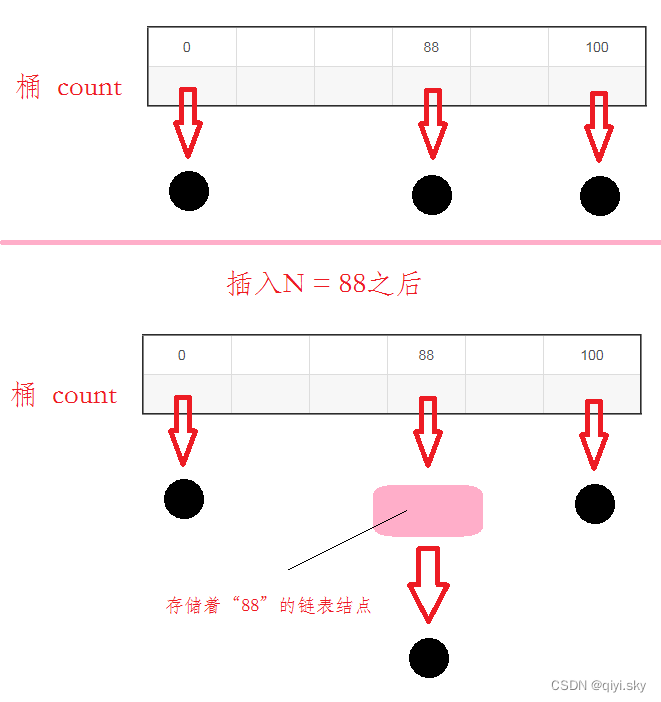
假设有N个学生,他们的成绩是0到100之间的整数(于是有M=101个不同的成绩值)。如何在线性时间内将学生按成绩排序?
桶排序的处理方法是:
建立M个桶,一开始初始化为空链表;插入成绩值时,找到对应的桶,链接到对应的桶里面。
图示
伪代码
void Bucket_Sort(ElementType A[], int N)
{
count[]初始化;
while(读入1个学生的成绩grade)
{
将该生插入count[grade]链表;
}
for(i = 0; i < M; i++)
{
if(count[i])
输出整个count[i]链表;
}
}时间复杂度
这个桶排序的时间复杂度很好分析,从伪代码上看是两个循环,一个读入N个学生的成绩,一个输出链表里的M个元素,所以:
如果,例如有101个不同的成绩值,但是要排序的学生只有5个,那么再用桶排序去建立101个桶就显得很浪费了,这个时候就引进我们的基数排序~
基数排序
事实上,基数排序是桶排序的升级版。我们先看一个例子:
假设我们有N = 10个整数,每个整数的值在0到999之间(于是有M=1000个不同的值)。还有可能在线性时间内排序吗?
输入序列:64,8,216,512,27,729,0,1,343,125。
这里用“次位优先”(Least Significant Digit) ,简称LSD。
次位优先的意思是说:从个位开始往高位比较。例如:一个三位数就是先比较个位,再比较十位,最后比较百位;与之相反的则是先比较百位,再比较十位,最后比较个位,即
“主位优先”(Most Significant Digit),简称MSD。
据题意可知,我们需要排序十个整数,故而建立十个桶,然后第一趟依据个位数进行排序:
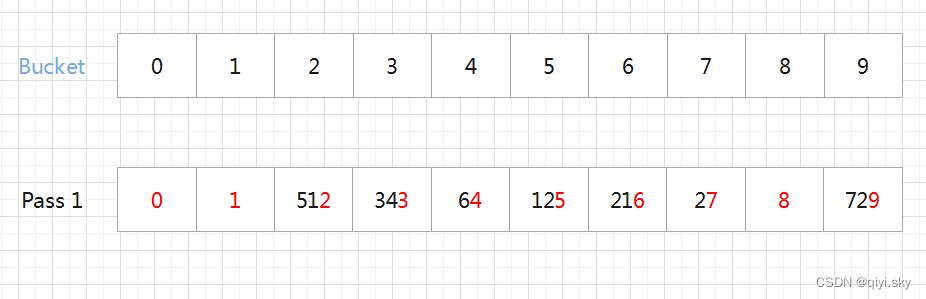
第二趟依据十位数进行排序: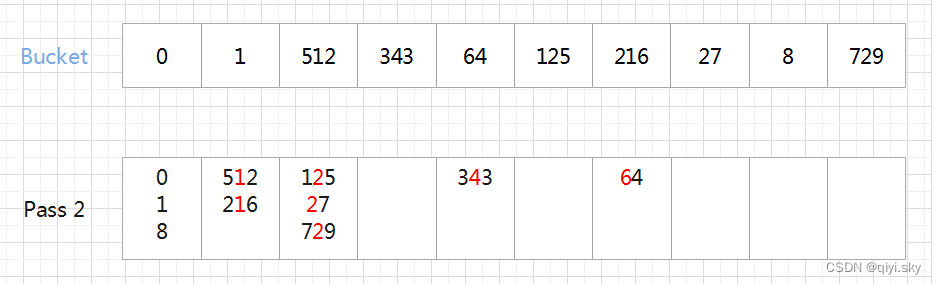
将排序结果收集起来:
最后一趟依据百位数来进行排序:

最后再收集结果,就得到我们的有序序列了:

如此,就完成了一次次位优先的基数排序。
时间复杂度:
N为需要收集排序的整数个数,B为桶的个数,P为排序的趟次。
多关键字排序
类似于扑克牌,一副扑克牌是按2种关键字排序的:
[花色]
![]()
[面值]
![]()
有序结果:![]()
用“主位优先”MSD排序:先为花色建4个桶,在每个桶内分别排序,最后合并结果。
用“次位优先”LSD排序:先为面值建13个桶,将结果合并,然后再为花色建4个桶。
代码(C语言)
代码链接:数据结构_浙江大学_中国大学MOOC(慕课)
次位优先
/* 基数排序 - 次位优先 */
/* 假设元素最多有MaxDigit个关键字,基数全是同样的Radix */
#define MaxDigit 4
#define Radix 10
/* 桶元素结点 */
typedef struct Node *PtrToNode;
struct Node {
int key;
PtrToNode next;
};
/* 桶头结点 */
struct HeadNode {
PtrToNode head, tail;
};
typedef struct HeadNode Bucket[Radix];
int GetDigit ( int X, int D )
{ /* 默认次位D=1, 主位D<=MaxDigit */
int d, i;
for (i=1; i<=D; i++) {
d = X % Radix;
X /= Radix;
}
return d;
}
void LSDRadixSort( ElementType A[], int N )
{ /* 基数排序 - 次位优先 */
int D, Di, i;
Bucket B;
PtrToNode tmp, p, List = NULL;
for (i=0; i<Radix; i++) /* 初始化每个桶为空链表 */
B[i].head = B[i].tail = NULL;
for (i=0; i<N; i++) { /* 将原始序列逆序存入初始链表List */
tmp = (PtrToNode)malloc(sizeof(struct Node));
tmp->key = A[i];
tmp->next = List;
List = tmp;
}
/* 下面开始排序 */
for (D=1; D<=MaxDigit; D++) { /* 对数据的每一位循环处理 */
/* 下面是分配的过程 */
p = List;
while (p) {
Di = GetDigit(p->key, D); /* 获得当前元素的当前位数字 */
/* 从List中摘除 */
tmp = p; p = p->next;
/* 插入B[Di]号桶尾 */
tmp->next = NULL;
if (B[Di].head == NULL)
B[Di].head = B[Di].tail = tmp;
else {
B[Di].tail->next = tmp;
B[Di].tail = tmp;
}
}
/* 下面是收集的过程 */
List = NULL;
for (Di=Radix-1; Di>=0; Di--) { /* 将每个桶的元素顺序收集入List */
if (B[Di].head) { /* 如果桶不为空 */
/* 整桶插入List表头 */
B[Di].tail->next = List;
List = B[Di].head;
B[Di].head = B[Di].tail = NULL; /* 清空桶 */
}
}
}
/* 将List倒入A[]并释放空间 */
for (i=0; i<N; i++) {
tmp = List;
List = List->next;
A[i] = tmp->key;
free(tmp);
}
}主位优先
/* 基数排序 - 主位优先 */
/* 假设元素最多有MaxDigit个关键字,基数全是同样的Radix */
#define MaxDigit 4
#define Radix 10
/* 桶元素结点 */
typedef struct Node *PtrToNode;
struct Node{
int key;
PtrToNode next;
};
/* 桶头结点 */
struct HeadNode {
PtrToNode head, tail;
};
typedef struct HeadNode Bucket[Radix];
int GetDigit ( int X, int D )
{ /* 默认次位D=1, 主位D<=MaxDigit */
int d, i;
for (i=1; i<=D; i++) {
d = X%Radix;
X /= Radix;
}
return d;
}
void MSD( ElementType A[], int L, int R, int D )
{ /* 核心递归函数: 对A[L]...A[R]的第D位数进行排序 */
int Di, i, j;
Bucket B;
PtrToNode tmp, p, List = NULL;
if (D==0) return; /* 递归终止条件 */
for (i=0; i<Radix; i++) /* 初始化每个桶为空链表 */
B[i].head = B[i].tail = NULL;
for (i=L; i<=R; i++) { /* 将原始序列逆序存入初始链表List */
tmp = (PtrToNode)malloc(sizeof(struct Node));
tmp->key = A[i];
tmp->next = List;
List = tmp;
}
/* 下面是分配的过程 */
p = List;
while (p) {
Di = GetDigit(p->key, D); /* 获得当前元素的当前位数字 */
/* 从List中摘除 */
tmp = p; p = p->next;
/* 插入B[Di]号桶 */
if (B[Di].head == NULL) B[Di].tail = tmp;
tmp->next = B[Di].head;
B[Di].head = tmp;
}
/* 下面是收集的过程 */
i = j = L; /* i, j记录当前要处理的A[]的左右端下标 */
for (Di=0; Di<Radix; Di++) { /* 对于每个桶 */
if (B[Di].head) { /* 将非空的桶整桶倒入A[], 递归排序 */
p = B[Di].head;
while (p) {
tmp = p;
p = p->next;
A[j++] = tmp->key;
free(tmp);
}
/* 递归对该桶数据排序, 位数减1 */
MSD(A, i, j-1, D-1);
i = j; /* 为下一个桶对应的A[]左端 */
}
}
}
void MSDRadixSort( ElementType A[], int N )
{ /* 统一接口 */
MSD(A, 0, N-1, MaxDigit);
}end
学习自:MOOC数据结构——陈越、何钦铭