一、前缀树是什么

前缀树是一种查找结构，常用于指定字符串或是数组、线性表等连续信息的存储和查找。
他的作用类似于哈希表，但是它相对于哈希表来说，限制更多，通用性较差，但是它的功能更加强大，可定制性也更强。

二、简单前缀树的结构分析

如需理解以下内容，首先你需要了解树的结构；

比如二叉树，父节点之下包含两个节点，分别为左右子节点，分别开辟空间，进行数据存储。
前缀树的结构也是类似的，它的每个节点包含两个部分: 值部分和指针部分。
它的存储方式为：在一棵树上，从根到子节点，分别存储所有目标数据的每一个下标位置上的数据
值部分主要又包含两个数据: 路过该节点的数量为pass， 以该节点为结尾的数量为end。
指针部分主要包含它的所有子节点，记为next

以存储26个小写英文字母为例，现在需要存储英文单词"ass"，则存储路径如下：
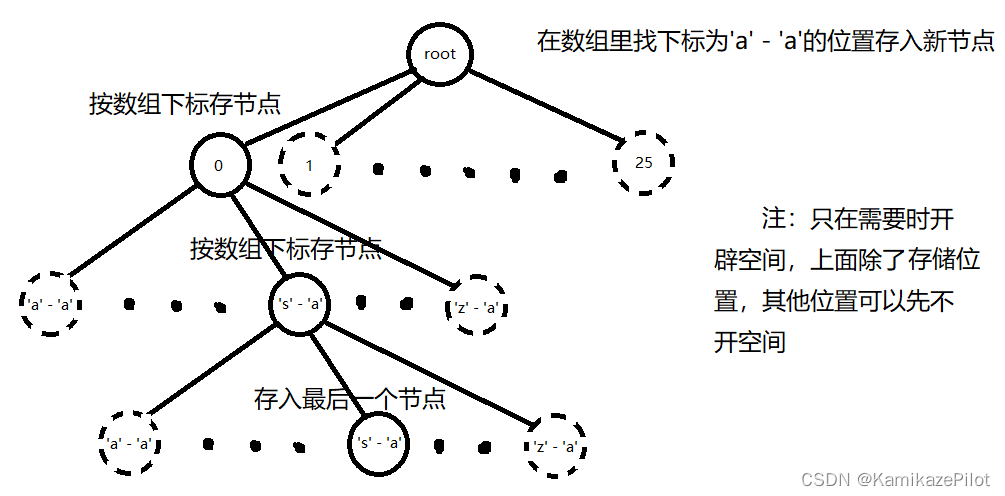
上图中，每经过一个节点，将该节点的pass值加一，将末尾节点的end值加一。通过这种操作记录所有经过的数据记录。
同时在树中，需要一个根节点来管理所有子节点，根节点中不存数据（除非是空字符串）
接下来就只需要用代码将所有方法实现即可

下面给出实现，一共四个接口：

insert插入字符串，给前缀树添加一组数据
find查找已存入的字符串个数
findContain 输入前缀查找已存在的前缀相同的字符串个数
erase 从前缀树中擦除一个字符串及其所存在数据

其中insert方法需要注意pass的数据增加
erase方法需要注意的是：
需要先检查字符串是否存在；
当一个节点的经过数量等于0时，即pass == 0 时，代表其下没有任何可能存在的字符串，所以直接将整棵树删除即可；
移除节点时，需要提前写好析构函数，将其所有子节点的内存全部释放，以免出现内存泄漏

代码：

#include <iostream>
using namespace std;
//26 个小写英文字母
#define NUMBER 26

// 节点的结构
class TrieNode
{
public:
	int pass;
	int end;
	TrieNode* nexts[NUMBER];
	TrieNode()
	{
		pass = 0;
		end = 0;
		for (int i = 0; i < NUMBER; i++)
		{
			nexts[i] = nullptr;
		}
	}
	~TrieNode()
	{
		for (int i = 0; i < NUMBER; i++)
		{
			if (nexts[i]) delete nexts[i];
		}
	}
};

// 所调用的树结构
class TrieTree
{
	TrieNode* root = nullptr;
public:
	TrieTree()
	{
		root = new TrieNode();
	}
	// 插入
	void insert(string word)
	{
		TrieNode* cur = root;
		cout << word;
		for (int i = 0; i < word.size(); i++)
		{
			
			int num = word[i] - 'a';
			if (cur->nexts[num] == nullptr)
			{
				cur->nexts[num] = new TrieNode();
			}
			cur = cur->nexts[num];
			cur->pass++;
		}
		cur->end++;
	}
	//查找字符串数量
	int find(string word)
	{
		TrieNode* cur = root;
		for (int i = 0; i < word.size(); i++)
		{
			int num = word[i] - 'a';
			if (cur->nexts[num] == nullptr) return 0;

			cur = cur->nexts[num];
		}
		return cur->end;
	}
	//查找前缀数量
	int findContain(string word)
	{
		TrieNode* cur = root;
		for (int i = 0; i < word.size(); i++)
		{
			int num = word[i] - 'a';
			if (cur->nexts[num] == nullptr) return 0;

			cur = cur->nexts[num];
		}
		return cur->pass;
	}
	//删除
	bool erase(string word)
	{
		if (find(word) == 0) return false;
		TrieNode* cur = root;
		for (int i = 0; i < word.size(); i++)
		{
			int num = word[i] - 'a';

			if (cur->nexts[num]->pass <= 1)
			{
				delete cur->nexts[num];
				cur->nexts[num] = nullptr;
				return true;
			}
			cur = cur->nexts[num];
			cur->pass--;
		}
		cur->end--;
		return true;
	}
};