前言
因为各种各样的原因要开始学习深度学习了,跟着吴恩达老师的深度学习视频,自己总结一些知识点,以及学习中遇到的一些问题,以便记录学习轨迹以及以后复习使用,为了便于自己理解,我会将一些知识点用以个人的理解用通俗的语言表达出来,如果有错误,请大家指出。
线性回归
说到逻辑回归,不得不提一下与逻辑回归思想相类似的线性回归
定义
线性回归是一种用于建立输入特征和输出之间线性关系的统计学和机器学习算法。它的目标是通过已知的特征值和相应的输出值(或称为标签、响应变量),拟合一条直线(在一维情况下)或超平面(在多维情况下),以最好地预测未知样本的输出值。
用处
那么线性回归要解决一个什么问题呢?线性回归可以用于预测一个或多个连续数值型的目标变量。例如:预测房价,温度,销售额。
条件
-
目标变量是连续的
-
特征与目标变量之间存在线性关系
什么叫线性相关呢?举一个只包含一个自变量和一个因变量的例子,例如:房价与房子面积,控制其他变量的情况下,房子面积越大,房价越高,且如果将 面积作为x,房价作为y,在坐标轴上画出函数曲线将是一条直线。
房价不仅仅只是由于一个因素影响,因此光通过面积来预测房价,显然是不准确的,可能还有地理位置,客厅数,层高等等,而这些因素里面,可能包含着因变量和自变量非线性关系的因素,例如:层高过低和过高,房价较低,层高在中间段的房价较高,显然,这不是一个线性关系,线关系至少应该是单调的。因此我们不能将层高作为参数放在线性回归模型中。
综上,判断一个问题是否适合线性回归法的时候,因先估测 自变量 与 因变量之间的关系是否符合线性相关。
-
特征之间相互独立
线性回归要求特征之间相互独立。如果特征之间存在较强的相关性,可能会影响线性回归模型的稳定性和解释性。举例:
假设我们有一个数据集,其中包含学生的学习成绩和每周学习时间两个特征,以及他们最终考试成绩作为目标变量。数据可能如下所示:
学习时间(小时/周) 学习成绩(分) 最终考试成绩(分) 5 80 85 6 90 88 3 70 78 4 75 80 在这个例子中,学习时间和学习成绩之间可能存在一定程度的相关性,因为通常情况下,学习时间越长,学习成绩可能越好。然而,如果学习时间和学习成绩之间存在高度的相关性,比如说学习时间和学习成绩完全线性相关(一个完全可以由另一个预测得出),那么这两个特征就不是相互独立的。
相互独立的特征在线性回归中是非常重要的,因为线性回归模型是基于特征之间的线性组合来建模的。如果特征之间存在多重共线性(高度相关),那么模型就可能变得不稳定,而且在预测新数据时可能会产生较大的误差。
对于上述例子,如果学习时间和学习成绩之间存在高度的线性相关性,那么线性回归模型可能会过度依赖其中一个特征,而忽略另一个特征的影响。这将导致模型失去泛化能力,对新的未知数据表现较差。
-
数据的误差项满足常态分布
-
数据中不存在明显的异常值
线性回归对异常值敏感,特别是在样本量较小时更容易受到影响。因此,在使用线性回归之前,需要对数据进行异常值检测和处理。
-
数据量较大
线性回归通常在大样本量下表现较好。样本量较小时,模型可能过于简单,拟合效果不佳。
-
问题的复杂性
线性回归适用于简单的问题,当问题非常复杂且特征与目标之间存在非线性关系时,其他更复杂的模型可能更为合适。
公式
y = w T x + b y = w^T x + b y=wTx+b
以上为线性回归的矩阵形式的公式,其中 w ,x ,b都是向量
-
y是输出
-
x 是输入特征的向量,表示为 [ x 1 , x 2 , . . . x m ] [x_1,x_2,...x_m] [x1,x2,...xm]
-
w 是权重参数的向量,表示为 [ w 1 , w 2 , . . . w n ] [w_1,w_2,...w_n] [w1,w2,...wn]
-
w T w^T wT是权重参数向量的转置
-
b 是偏置参数(截距)
为什么w要转置呢?w与x都是行向量,矩阵乘法的规则要求第一个矩阵的列数和第二个矩阵的行数相等,因此要将w转置,才可以进行矩阵运算
y
=
w
1
×
x
1
+
w
2
×
x
2
+
.
.
.
+
w
n
×
x
n
+
b
y = w1 \times x1 + w2 \times x2 + ... + w_n \times x_n + b
y=w1×x1+w2×x2+...+wn×xn+b
。不使用矩阵的公式 结果更易于理解,
w
n
w_n
wn越大代表第n个特征在y中的权重越高,即因素n对于预测y越重要。
训练方法
最小二乘法:通过最小化预测值与实际观测值之间的残差平方和来拟合回归系数。
思路:找到一条直线,使得所有数据点到这条直线的距离之和最小,也就是使得所有数据点的残差平方和最小
逻辑回归
定义
逻辑回归是一种用于解决二分类问题的监督学习算法。在逻辑回归中,我们试图建立一个线性模型,将自变量(特征)与因变量(目标变量)之间的关系映射为一个概率值,然后根据概率值进行分类预测。
用途
解决二分类问题,即预测样本属于两个类别中的哪一个,例如,判断一封电子邮件是垃圾邮件还是非垃圾邮件,判断患者是否患有某种疾病等。
公式
z = w T x + b z = w^T x + b z=wTx+b
逻辑回归的前提与线性回归类似,需要特征与目标变量之间存在线性关系,可以看出与线性回归是完全相同的,由此函数得出的是一个数值,该数值可以是任意实数。
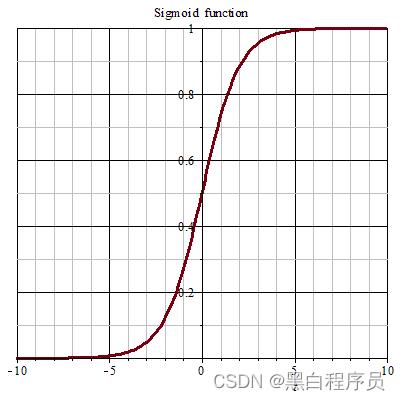
由于我们要解决一个二分类问题,实现的手段是需要样本在经过模型计算后,输出是否属于该类的概率值。概率的取值范围是**[0-1]**,因此需要将线性函数,映射到一个值域范围为0-1的函数上,因此我们需要使用 sigmoid函数,其函数表达式与图像如下
σ
(
x
)
=
1
1
+
e
−
t
\sigma(x) = \frac{1}{1+e^{-t}}
σ(x)=1+e−t1
使用 sigmoid函数的原因
- 概率解释:**sigmoid函数是一个将实数映射到 0 到 1 之间的函数。**在逻辑回归中,我们希望输出的结果可以解释为样本属于某一类别的概率。通过sigmoid函数,线性模型的输出值可以被解释为样本属于正类的概率。例如,当sigmoid函数的输出值为0.7时,表示样本属于正类的概率是0.7,属于负类的概率是0.3。
- 易于分类:通过设定一个阈值,通常是0.5,我们可以将sigmoid函数的输出结果二值化,使得样本可以被分为两个类别(0或1)。当sigmoid函数的输出大于阈值时,将样本预测为正类(1),否则预测为负类(0)。这样,逻辑回归可以用于二分类问题。
- 平滑性:sigmoid函数具有平滑的性质,在0和1两端有平缓的曲线。这样的平滑性使得逻辑回归在数值计算和优化过程中更加稳定和高效。
- 可微性:sigmoid函数是一个可微函数,这在梯度下降等优化算法中是必要的。逻辑回归使用梯度下降来估计回归系数,使得模型能够逐步优化拟合训练数据。
- 凸性:逻辑回归的损失函数在回归系数空间中是一个凸函数,这保证了在训练过程中能够找到全局最优解,而不会陷入局部最优解。
y ^ = σ ( w T + b ) \hat{y} = \sigma(w^T+b) y^=σ(wT+b)
将函数z映射到sigmoid函数上,得到概率 y ^ \hat{y} y^ , y ^ \hat{y} y^ 代表该样本属于该类的概率,这就是我们逻辑回归的模型。
训练过程
目标
目的是找出最佳的参数集合
{
w
1
,
w
2
,
.
.
.
,
w
n
}
\{w_1,w_2,...,w_n\}
{w1,w2,...,wn}(n为特征的维度)以及偏差b,使得
y
^
\hat{y}
y^ 更接近于 实际标签
y
(
i
)
y^{(i)}
y(i),上标(i)代表第i个特征,
y
(
i
)
y^{(i)}
y(i)代表第i个特征的是否属于该类,属于则数值为1,不属于则数值为0。
G
i
v
e
n
{
(
x
1
,
y
1
)
,
.
.
.
,
(
x
m
,
y
m
)
}
,
w
a
n
t
y
^
≈
y
(
i
)
Given\{(x^1,y^1),...,(x^m,y^m)\},want\,\hat{y}\approx y^{(i)}
Given{(x1,y1),...,(xm,ym)},wanty^≈y(i)
损失函数
损失函数用来衡量算法在单个训练样本中得表现如何,通过最小化(或最大化)损失函数来找到模型的最优参数或最优解。
逻辑回归中,要使用到的损失函数是
L
(
y
^
,
y
)
=
−
y
log
(
y
^
)
−
(
1
−
y
)
log
(
1
−
y
^
)
L(\hat{y},y) = -y\log(\hat{y}) - (1-y)\log(1-\hat{y})
L(y^,y)=−ylog(y^)−(1−y)log(1−y^)
首先看这个函数 符不符合要求。
当 y = 1 时 L = − log ( y ^ ) L = -\log(\hat{y}) L=−log(y^) ,如果要想使得损失函数L尽可能小,则 y ^ \hat{y} y^要尽可能大,由于 y ^ \hat{y} y^的取值是0-1,因此 y ^ \hat{y} y^无限接近于1时,此时L无限接近0
当y = 0 时 L = − log ( 1 − y ^ ) L = -\log(1-\hat{y}) L=−log(1−y^),如果要想使得损失函数L尽可能小,则 y ^ \hat{y} y^要尽可能小,由于 y ^ \hat{y} y^的取值是0-1,因此 y ^ \hat{y} y^无限接近于0 时,此时L无限接近0
该函数,满足上述条件 G i v e n { ( x 1 , y 1 ) , . . . , ( x m , y m ) } , w a n t y ^ ≈ y ( i ) Given\{(x^1,y^1),...,(x^m,y^m)\},want\,\hat{y}\approx y^{(i)} Given{(x1,y1),...,(xm,ym)},wanty^≈y(i),因此可以作为损失函数使用。
损失函数推导
再看看上述损失函数是如何得出的
y
^
=
σ
(
z
)
=
σ
(
w
T
x
+
b
)
=
1
1
+
e
−
z
\hat{y} = \sigma(z) = \sigma(w^Tx+b) = \frac{1}{1+e^{-z}}
y^=σ(z)=σ(wTx+b)=1+e−z1
上式中的
y
^
\hat{y}
y^ 代表训练样本x条件下 y = 1的概率
换句话说 1 − y ^ 1-\hat{y} 1−y^ 即训练样本x条件下 y = 0 的概率
此时,概率满足 伯努利分布(0-1分布)
P
{
X
=
k
}
=
p
k
(
1
−
p
)
1
−
k
,
k
=
0
,
1
P\{ X = k \} = p^k(1-p)^{1-k},k = 0,1
P{X=k}=pk(1−p)1−k,k=0,1
将
p
=
y
^
,
k
=
y
p = \hat{y} ,k =y
p=y^,k=y 代入上式,得到
p
(
y
∣
x
)
=
y
^
y
(
1
−
y
^
)
1
−
y
,
y
=
0
,
1
p(y|x)= \hat{y}^y(1-\hat{y})^{1-y},y = 0,1
p(y∣x)=y^y(1−y^)1−y,y=0,1
由于假设所有的m个训练样本服从同一分布且相互独立,也即独立同分布的,所有这些样本的联合概率就是每个样本概率的乘积:
P
(
l
a
b
e
l
s
i
n
t
r
a
i
n
i
n
g
s
e
t
)
=
∏
1
=
i
m
P
(
y
(
i
)
∣
x
(
i
)
)
P(labels\,in\,training\,set)=\prod_{1=i}^{m}P(y^{(i)}|x^{(i)})
P(labelsintrainingset)=1=i∏mP(y(i)∣x(i))
此时,对该函数进行 最大似然估计(寻找一组参数,使得给定样本的观测值概率最大,即寻找一组
{
w
1
,
w
2
,
.
.
.
w
n
}
\{w1,w2,...w_n\}
{w1,w2,...wn},使得输入
{
x
1
,
x
2
,
.
.
.
x
m
}
\{x1,x2,...x_m\}
{x1,x2,...xm}得到
y
^
\hat{y}
y^的概率最大),为了方便运算,取对数似然函数,化乘法为加法
log
P
(
l
a
b
e
l
s
i
n
t
r
a
i
n
i
n
g
s
e
t
)
=
log
∏
1
=
i
m
P
(
y
(
i
)
∣
x
(
i
)
)
=
log
∑
i
=
1
m
P
(
y
(
i
)
∣
x
(
i
)
)
\log P(labels\,in\,training\,set)=\log\prod_{1=i}^{m}P(y^{(i)}|x^{(i)}) =\log\sum_{i=1}^{m}P(y^{(i)}|x^{(i)})
logP(labelsintrainingset)=log1=i∏mP(y(i)∣x(i))=logi=1∑mP(y(i)∣x(i))
我们发现对第i个样本取对数
log
p
(
y
(
i
)
∣
x
(
i
)
)
=
log
(
y
^
y
(
i
)
(
1
−
y
^
)
1
−
y
(
i
)
)
=
y
(
i
)
l
o
g
(
y
^
)
+
(
1
−
y
(
i
)
)
log
(
1
−
y
^
)
=
−
L
(
y
^
,
y
(
i
)
)
\log p(y^{(i)}|x^{(i)})= \log(\hat{y}^{y^{(i)}}(1-\hat{y})^{1-{y^{(i)}}})=y^{(i)}log(\hat{y})+(1-y^{(i)})\log(1-\hat{y}) = -L(\hat{y},y^{(i)})
logp(y(i)∣x(i))=log(y^y(i)(1−y^)1−y(i))=y(i)log(y^)+(1−y(i))log(1−y^)=−L(y^,y(i))
因此对数似然估计可简化为
log
P
(
l
a
b
e
l
s
i
n
t
r
a
i
n
i
n
g
s
e
t
)
=
−
log
∑
i
=
1
n
L
(
y
^
,
y
(
i
)
)
\log P(labels\,in\,training\,set) =-\log\sum_{i=1}^{n}L(\hat{y},y^{(i)})
logP(labelsintrainingset)=−logi=1∑nL(y^,y(i))
为了使用梯度下降法,我们需要将问题转化为最小化问题,因此我们的问题转化为求
∑
i
=
1
n
L
(
y
^
,
y
(
i
)
)
\sum_{i=1}^{n}L(\hat{y},y^{(i)})
∑i=1nL(y^,y(i))的最小值
代价函数
为了衡量算法在全部训练样本上得表现如何,我们需要定义一个算法得代价函数,使得算法在所有样本上表现的最好,因此我们取所有样本的损失函数的平均值。
J
(
w
,
b
)
=
1
n
∑
i
=
1
n
L
(
y
^
,
y
(
i
)
)
J(w,b) = \frac{1}{n}\sum_{i = 1}^{n}L(\hat{y},y^{(i)})
J(w,b)=n1i=1∑nL(y^,y(i))
得到上述公式后,我们最后的目标就转化为了找到一组w和b,使得代价函数最小。
梯度下降法
逻辑回归使用梯度下降法进行训练,核心思想是沿着函数的负梯度方向进行迭代更新,从而逐步接近或到达最优解。梯度是函数在某一点处的变化率和方向,负梯度方向指向函数下降最快的方向。在梯度下降法中,通过计算函数的梯度,确定当前点的下降方向,并根据**学习率(步长)**控制每一步的大小,逐步调整自变量的取值,直至找到最优解或达到迭代次数上限。
根据梯度下降法的核心思想,我们可以得出公式
w
:
=
w
−
a
∂
J
(
w
,
b
)
∂
w
,
b
:
=
b
−
a
∂
J
(
w
,
b
)
∂
b
w:=w-a\frac{\partial{J(w,b)}}{\partial{w}},b:=b-a\frac{\partial{J(w,b)}}{\partial{b}}
w:=w−a∂w∂J(w,b),b:=b−a∂b∂J(w,b)
只考虑单个样本的情况,损失函数L对
y
^
\hat{y}
y^求导得
d
L
d
y
^
=
−
y
y
^
+
1
−
y
1
−
y
^
(
1
)
\frac{dL}{d\hat{y}} = - \frac{y}{\hat{y}}+\frac{1-y}{1-\hat{y}} \ \ (1)
dy^dL=−y^y+1−y^1−y (1)
d y ^ d z = d ( 1 1 + e − z ) z = − 1 ( 1 + e − z ) 2 + ( − e ) − z = 1 1 + e − z × e − z 1 + e − z = 1 1 + e − z × ( 1 − 1 1 + e − z ) = y ^ ( 1 − y ^ ) ( 2 ) \frac{d\hat{y}}{dz} = \frac{d(\frac{1}{1+e^{-z}})}{z} = - \frac{1}{(1+e^{-z})^2} + (-e)^{-z} =\frac{1}{1+e^{-z}}\times\frac{e^{-z}}{1+e^{-z}} =\frac{1}{1+e^{-z}}\times(1-\frac{1}{1+e^{-z}}) = \hat{y}(1-\hat{y}) \ \ (2) dzdy^=zd(1+e−z1)=−(1+e−z)21+(−e)−z=1+e−z1×1+e−ze−z=1+e−z1×(1−1+e−z1)=y^(1−y^) (2)
由(1)(2)式可得
d
L
d
z
=
(
d
L
d
y
^
)
(
d
y
^
d
z
)
=
(
−
y
y
^
+
1
−
y
1
−
y
^
)
(
y
^
(
1
−
y
^
)
)
=
−
y
(
1
−
y
^
)
+
y
^
(
1
−
y
)
=
y
^
−
y
\frac{dL}{dz} = (\frac{dL}{d\hat{y}})(\frac{d\hat{y}}{dz}) = (- \frac{y}{\hat{y}}+\frac{1-y}{1-\hat{y}} )(\hat{y}(1-\hat{y}) )=-y(1-\hat{y})+\hat{y}(1-y) = \hat{y} - y
dzdL=(dy^dL)(dzdy^)=(−y^y+1−y^1−y)(y^(1−y^))=−y(1−y^)+y^(1−y)=y^−y
由于
∂
L
∂
w
1
=
(
d
L
d
z
)
(
d
z
d
w
1
)
=
x
1
d
L
d
z
=
x
1
(
y
^
−
y
)
\frac{\partial{L}}{\partial{w_1}} = (\frac{dL}{dz})(\frac{dz}{dw_1}) =x_1 \frac{dL}{dz} = x_1(\hat{y}-y)
∂w1∂L=(dzdL)(dw1dz)=x1dzdL=x1(y^−y)
∂ L ∂ b = ( d L d z ) ( d z d b ) = d L d z = y ^ − y \frac{\partial{L}}{\partial{b}} = (\frac{dL}{dz})(\frac{dz}{db}) =\frac{dL}{dz} = \hat{y}-y ∂b∂L=(dzdL)(dbdz)=dzdL=y^−y
考虑所有样本得
∂
J
∂
w
1
=
1
m
x
1
(
i
)
∑
i
=
1
m
(
y
^
(
i
)
−
y
(
i
)
)
\frac{\partial{J}}{\partial{w_1}} = \frac{1}{m}x_1^{(i)}\sum_{i = 1}^{m}(\hat{y}^{(i)}-y^{(i)})
∂w1∂J=m1x1(i)i=1∑m(y^(i)−y(i))
其余参数以此类推
∂
J
∂
w
n
=
1
m
x
n
(
i
)
∑
i
=
1
m
(
y
^
(
i
)
−
y
(
i
)
)
\frac{\partial{J}}{\partial{w_n}} = \frac{1}{m}x_n^{(i)}\sum_{i = 1}^{m}(\hat{y}^{(i)}-y^{(i)})
∂wn∂J=m1xn(i)∑i=1m(y^(i)−y(i))
∂
J
∂
b
=
1
m
∑
i
=
1
m
(
y
^
(
i
)
−
y
(
i
)
)
\frac{\partial{J}}{\partial{b}} = \frac{1}{m}\sum_{i = 1}^{m}(\hat{y}^{(i)}-y^{(i)})
∂b∂J=m1i=1∑m(y^(i)−y(i))
最后带入最初的公式,即为一次梯度下降的结果
w
1
:
=
w
1
−
a
×
1
m
x
1
(
i
)
∑
i
=
1
m
(
y
^
(
i
)
−
y
(
i
)
)
w1:=w1-a\times\frac{1}{m}x_1^{(i)}\sum_{i = 1}^{m}(\hat{y}^{(i)}-y^{(i)})
w1:=w1−a×m1x1(i)i=1∑m(y^(i)−y(i))
以此类推
w
n
:
=
w
n
−
a
×
1
m
x
1
(
i
)
∑
i
=
1
m
(
y
^
(
i
)
−
y
(
i
)
)
w_n:=w_n-a\times\frac{1}{m}x_1^{(i)}\sum_{i = 1}^{m}(\hat{y}^{(i)}-y^{(i)})
wn:=wn−a×m1x1(i)∑i=1m(y^(i)−y(i))
b
:
=
b
−
a
×
1
m
∑
i
=
1
m
(
y
^
(
i
)
−
y
(
i
)
)
b:=b-a\times \frac{1}{m}\sum_{i = 1}^{m}(\hat{y}^{(i)}-y^{(i)})
b:=b−a×m1i=1∑m(y^(i)−y(i))