典型相关分析(Canonical Correlation analysis)研究两组变量(每组变量中都可能有多个指标)之间相关关系的一种多元统计方法。它能够揭示出两组变量之间的内在联系。
例子:

典型相关分析定义:
列题分析:
思路:
多元统计:(本部分只做一些了解,博主目前还涉及统计概率学,只能放一些ppt)
- 引言:

- 典型相关分析的基本思想:




(下面这两幅图符合我们高中数学的ka方检验)当计算结果<ka方时则没有相关性,反之有相关性。


标准化后的相关变量:
典型荷载分析: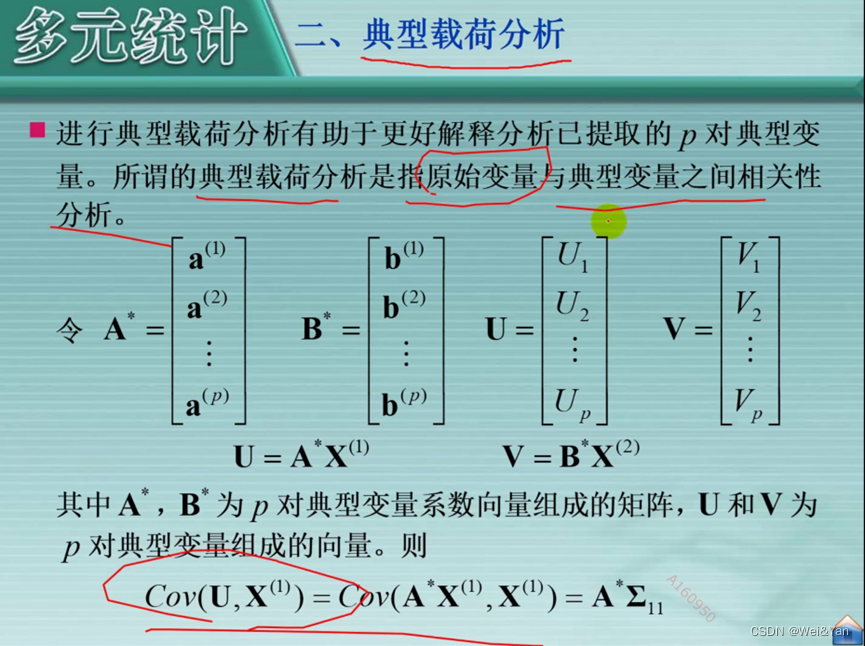
典型冗余分析:

典型相关分析的关键步骤:






典型相关分析在spss中的应用
(我们在解决问题的时候通常利用spss来帮我们进项计算,统计)
步骤:

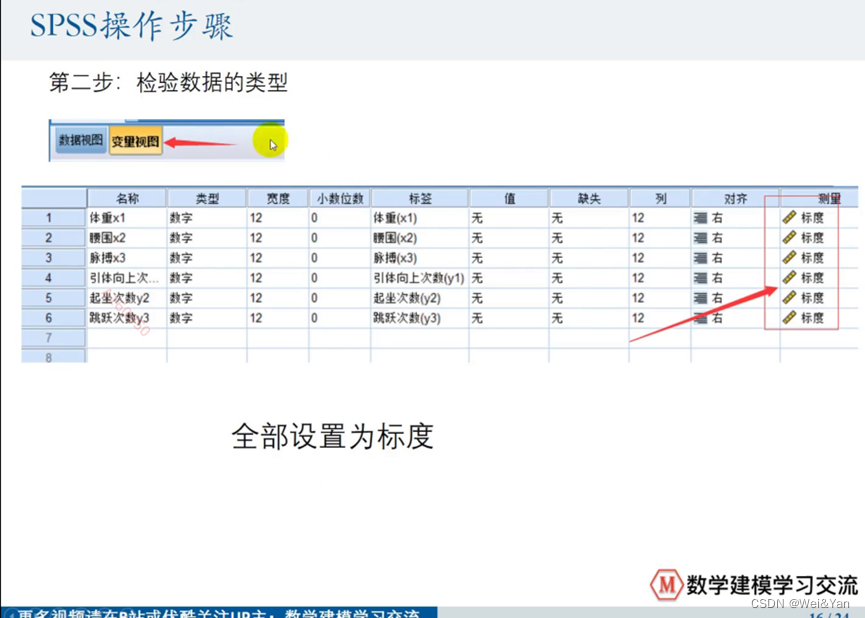



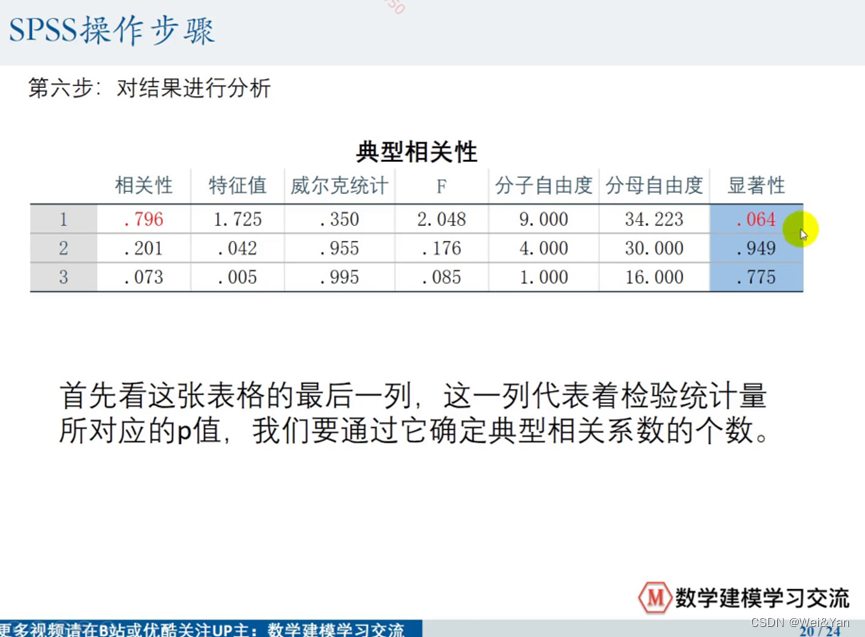
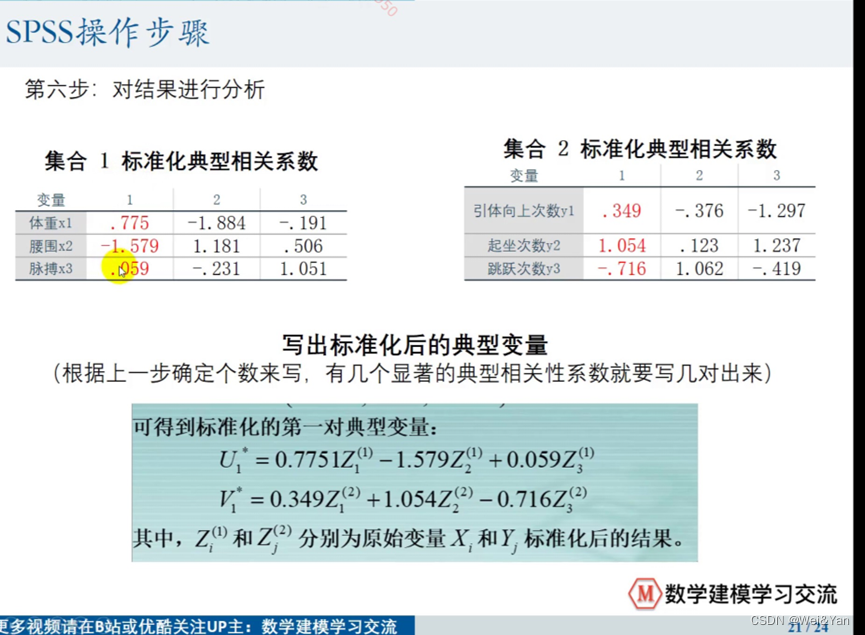
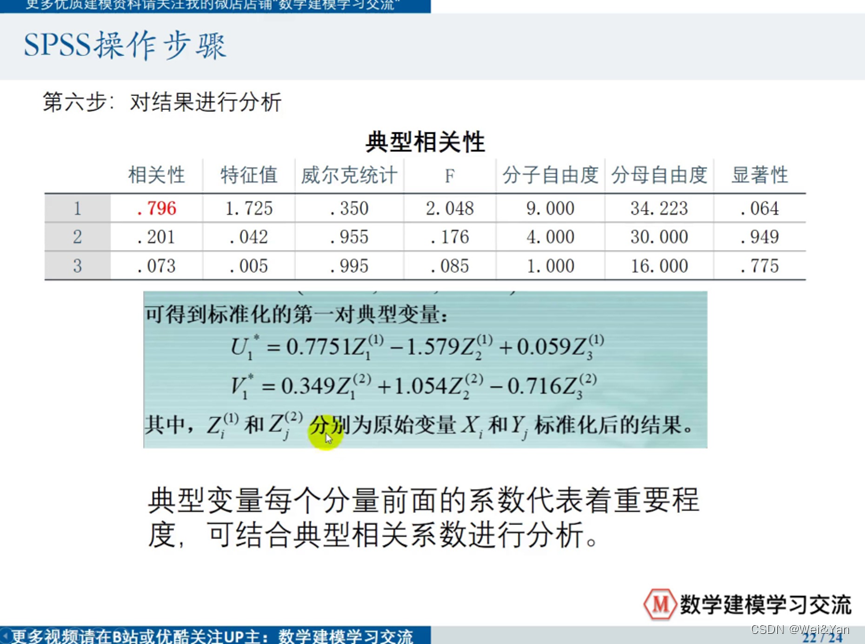

spss导出后,如果要写在论文中需要一些名称的修改:
讲典型相关性修改为->典型相关系数,显著性->p值
标准化典型相关系数->标准化典型相关变量对应的线性组合
我们讲最开始电视评分作为例子用spss实现:
GET DATA
/TYPE=XLSX
/FILE='C:\Users\kay21\OneDrive\文档\典型相关分析.xlsx'
/SHEET=name 'Sheet1'
/CELLRANGE=FULL
/READNAMES=ON
/DATATYPEMIN PERCENTAGE=95.0
/HIDDEN IGNORE=YES.
EXECUTE.
DATASET NAME 数据集1 WINDOW=FRONT.
STATS CANCORR SET1=led hed net SET2=arti com man
/OPTIONS COMPUTECVARS=NO
/PRINT PAIRWISECORR=NO LOADINGS=YES VARPROP=YES COEFFICIENTS=YES.
Canonical Correlations
| 备注 | ||
| 已创建输出 | 19-JUL-2023 10:45:14 | |
| 注释 | ||
| 输入 | 活动数据集 | 数据集1 |
| 过滤器 | <无> | |
| 权重 | <无> | |
| 拆分文件 | <无> | |
| 语法 | BEGIN PROGRAM '# '. | |
| 资源 | 处理程序时间 | 00:00:00.02 |
| 耗用时间 | 00:00:00.05 | |
[数据集1]
| 典型相关性设置 | |
| 值 | |
| 集合 1 变量 | led hed net |
| 集合 2 变量 | arti com man |
| 集中的数据集 | 无 |
| 评分语法 | 无 |
| 用于评分的相关性 | 3 |
| 典型相关系数 | |||||||
| 相关性 | 特征值 | 威尔克统计 | F | 分子自由度 | 分母自由度 | P值 | |
| 1 | .995 | 108.911 | .000 | 141.580 | 9.000 | 58.560 | .000 |
| 2 | .953 | 9.854 | .055 | 40.940 | 4.000 | 50.000 | .000 |
| 3 | .637 | .684 | .594 | 17.784 | 1.000 | 26.000 | .000 |
| H0 for Wilks 检验是指当前行和后续行中的相关性均为零 |
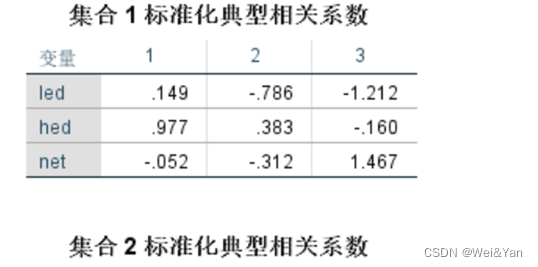
| 集合 1 标准化典型相关变量对应的线性组合 | |||
| 变量 | 1 | 2 | 3 |
| led | .149 | -.786 | -1.212 |
| hed | .977 | .383 | -.160 |
| net | -.052 | -.312 | 1.467 |
| 集合 2 标准化典型相关变量对应的线性组合 | |||
| 变量 | 1 | 2 | 3 |
| arti | .858 | .911 | -1.983 |
| com | .019 | -1.046 | -1.114 |
| man | .145 | -.337 | 2.833 |
| 集合 1 非标准化典型相关变量对应的线性组合 | |||
| 变量 | 1 | 2 | 3 |
| led | .007 | -.035 | -.054 |
| hed | .032 | .012 | -.005 |
| net | -.002 | -.013 | .059 |
| 集合 2 非标准化典型相关变量对应的线性组合 | |||
| 变量 | 1 | 2 | 3 |
| arti | .029 | .030 | -.066 |
| com | .001 | -.046 | -.049 |
| man | .006 | -.014 | .117 |
| 集合 1 典型载荷 | |||
| 变量 | 1 | 2 | 3 |
| led | .333 | -.925 | -.185 |
| hed | .993 | .101 | .057 |
| net | .383 | -.753 | .535 |
| 集合 2 典型载荷 | |||
| 变量 | 1 | 2 | 3 |
| arti | .997 | .065 | -.043 |
| com | .571 | -.811 | -.126 |
| man | .922 | -.274 | .273 |
| 集合 1 交叉载荷 | |||
| 变量 | 1 | 2 | 3 |
| led | .331 | -.881 | -.118 |
| hed | .989 | .096 | .036 |
| net | .381 | -.718 | .341 |
| 集合 2 交叉载荷 | |||
| 变量 | 1 | 2 | 3 |
| arti | .992 | .062 | -.028 |
| com | .568 | -.773 | -.080 |
| man | .918 | -.261 | .174 |
| 已解释的方差比例 | ||||
| 典型变量 | 集合 1 * 自身 | 集合 1 * 集合 2 | 集合 2 * 自身 | 集合 2 * 集合 1 |
| 1 | .415 | .411 | .723 | .717 |
| 2 | .478 | .434 | .246 | .223 |
| 3 | .108 | .044 | .031 | .012 |




![[微信小程序] 关于自定义字体的坑](https://img-blog.csdnimg.cn/29fe463468d548dc9f53e830bda8e212.png)