C++进阶：map和set

news2025/5/16 21:48:42

map和set

STL容器分为序列式容器和关联式容器。

  • 序列式容器vector、list等底层为线性数据结构，数据元素之间没有联系，一般用来存储数据。
  • 关联式容器map、set等底层采用平衡搜索树，存储的是<key/value>式的键值对，数据检索效率高。

1.容器

1.1 set

template < class T,                        // T 元素数据类型
           class Compare = less<T>,        // compare 该数据类型的比较函数
           class Alloc = allocator<T>>     // Alloc 空间配置器
class set;

set就是K模型的容器，按照搜索树的规则存储元素，具有排序和去重的功能。

set等搜索树容器都不支持修改元素，会破坏搜索树结构。find的返回值被const修饰。

接口

增加解释
pair<iterator,bool> insert (const value_type& val)单个插入
iterator insert (iterator position, const value_type& val)迭代器插入
void insert (InputIterator first, InputIterator last)范围插入
set<int> s;
s.insert(3);
s.insert(1);
s.insert(5);
s.insert(8);
s.insert(8);
s.insert(2);
s.insert(2);

std::set<int>::iterator it = s.begin();
while (it != s.end()) {
    cout << *it << " ";
    ++it;
}
// 1 2 3 5 8 //set底层是平衡搜索树，所以可以去重和排序
删除解释
size_type erase (const value_type& val)指定值删除
void erase (iterator position)迭代器删除
void erase (iterator first, iterator last)范围删除

值删除接口返回的是删除元素的个数，可通过此判断是否删除成功。

size_t ret = s.erase(30);
std::cout << ret << std::endl; // 使用值删除时，返回值是删除元素的个数
查找解释
iterator find (const value_type& val) const值查找
size_type count (const value_type& val) const返回个数
set<int>::iterator pos = s.find(30);
if (pos != s.end())
    s.erase(pos);

int cnt = s.count(30);
if (cnt == 1)
    cout << "ok" << endl;

1.2 multiset

**multiset没有去重机制，允许键值重复。**其底层也是搜索树，插入相同元素时，可以放到该节点的任意子节点。

对于键值重复的节点，查找返回的是中序遍历遇到的第一个节点。

比如查找值为10的节点，在找到第一个10时，会到他的左子树去找，直到遇到比10小的数。

std::multiset<int> s;
s.insert(3);
s.insert(1);
s.insert(5);
s.insert(5);
s.insert(2);
s.insert(2);

multiset<int>::iterator it = s.begin();
while (it != s.end()) {
    std::cout << *it << " ";
    ++it;
}
// 1 2 2 3 5 5

接口

multiset<int>::iterator pos = s.find(1);
while (pos != s.end() && *pos == 1)
{
    s.erase(pos);
    ++pos;
}

删除和迭代器遍历操作不可以放在一起，删除就改变了原有树的结构，再++pos就访问非法空间了。可以用下面更简单的方式。

while (pos != s.end())
{
    s.erase(pos);
    std::cout << "找到了" << std::endl;
    pos = s.find(1);
}

int ret = 1;
while (ret)
{
    ret = s.erase(1);
    std::cout << "找到了" << std::endl;
}

 

1.3 map

map底层也是平衡搜索树，map的元素按照键值key进行排序。map支持下标访问符，可以找到与key对应的value。

定义

键值对是表示具有对应关系的一种结构，一般只有两个成员key和value，key代表键值，value表示对应的数据。

template <class T1, class T2>
struct pair
{
  typedef T1 first_type;
  typedef T2 second_type;
  first_type first;
  second_type second;
    
  pair(const T1& a, const T2& b) : first(a = T1()), second(b = T2())
  {}
};

pair就是键值对，实际上是一个结构体，被map当作元素类型使用。

template < class Key,                                     // map::key_type
           class T,                                       // map::mapped_type
           class Compare = less<Key>,                     // map::key_compare
           class Alloc = allocator<pair<const Key,T> >    // map::allocator_type
         > class map;

接口

typedef Key key_type;
typedef T mapped_type;
typedef pair<const Key, T> value_type;
增加解释
pair<iterator,bool> insert (const value_type& val)单个插入
dict.insert(pair<string, string>("arrary", "数组"));
dict.insert(make_pair("string", "字符串"));
dict.insert({"sort", "排序"});

auto ret = m.insert({"sort", "[[排序]]"});
cout <<(ret.first)->first << (ret.first)->second << ret.second << endl; // sort 排序 0

插入返回的是迭代器和布尔值的键值对。布尔值表示插入是否成功。

  • 树中无重复key值的元素则插入成功，迭代器表示插入位置。
  • 树中存在相同key值的元素则插入失败，迭代器表示该相同key值元素的位置。
查找解释
iterator find (const key_type& k)查找
string str;
while (cin >> str) {
    map<string, string>::iterator it = m.find(str);
    if (it != m.end()) {
        cout << it->first << "-" << it->second << endl;
    }
}
删除解释
size_type erase (const key_type& k)指定值删除
void erase (iterator position)迭代器删除
void erase (iterator first, iterator last)范围删除

erase删除节点可以传迭代器，也可以传key进行遍历删除。

下标访问解释
mapped_type& operator[] (const key_type& k)下标访问
mapped_type& at (const key_type& k)下标访问

[]基本功能是查找，此外兼具插入和修改。

count_map["pg"];         // 插入
cout << count_map["pg"]; // 查找
count_map["pg"] = 111;   // 修改
count_map["tz"] = 888;   // 插入+修改

调用insert，无则插入有则查找，返回value的引用表示支持修改。

他的内部实现是：

mapped_type& operator[] (const key_type& k)
{
    return insert(make_pair(k,mapped_type())).first->second;
    // pair<iterator, bool> ret = insert(make_pair(k, mapped_type()));
    // return ret.first->second;
}

string arr[] = {"西瓜","西瓜","苹果","西瓜","苹果","苹果","西瓜","苹果","香蕉","苹果","香蕉","梨"};
map<string, int> count_map;

for (auto& e : arr)
	count_map[e]++;
for (auto& kv: count_map)
	cout << kv.first << ": " << kv.second << endl;

1.4 multimap

multimap和map的区别是可存在重复数据。所以multimap无法重载[]操作符。

count可以用来统计同一key值元素的出现次数。

 

2. 底层结构

2.1 AVL树

AVL树的定义

搜索树的查找效率高，但如果数据有序或接近有序，搜索树就会退化成单支树，查找效率就会变成线性的。

使用AVL树插入新结点时会对树进行调整，保证每个结点的左右子树高度之差的绝对值不超过1。从而降低树的高度，减少平均搜索长度。

一棵AVL树要么是空树，要么是具有如下性质的搜索树：

  • 该树的左右子树都是AVL树，
  • 左右子树的高度之差（简称平衡因子）的绝对值不超过1。

在这里插入图片描述

使用平衡因子只是AVL树的一种实现方式。

这样的树是高度平衡的，它的高度维持在 l o g n logn logn 左右，搜索的时间复杂度就是 O ( l o g n ) O(logn) O(logn)。

template<class K, class V>
struct avl_node
{
    avl_node<K, V>* _left;
    avl_node<K, V>* _right;
    avl_node<K, V>* _parent;

    pair<K, V> _kv;
    int _bf; // balance factor

    avl_node<K, V>(const pair<K, V>& kv)
    	: _kv(kv), _bf(0), _left(nullptr), _right(nullptr), _parent(nullptr)
    {}
};

template<class K, class V>
class avl_tree
{
    typedef avl_node<K, V> node;
private:
    node* _root = nullptr;
};

AVL树的性能

AVL是一棵严格平衡的二叉搜索树，可以保证查询效率 O ( l o g n ) O(logn) O(logn) 。但插入删除时要维护平衡，会出现多次旋转，性能很低下。

因此，如果需要一种查询高效且有序的数据结构，且不常改变结构，可以考虑AVL树。AVL树在实际中不太常用，因为存在红黑树。

更新平衡因子

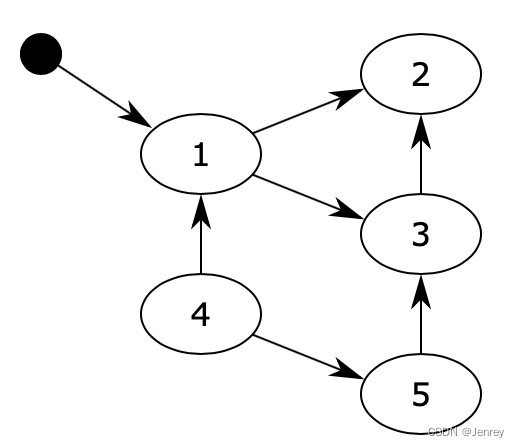
如图所示，插入节点会改变新节点到根的路径上所有节点的平衡因子。所以要先更新平衡因子，再对树旋转处理。

在这里插入图片描述

如果插入在父节点的左边，父节点的平衡因子要减1；如果插入在父节点的右边，父节点的平衡因子要加1。

  1. 如果父节点的平衡因子更新为0，说明所在树已经平衡且高度未变，不会影响到上层节点。
  2. 如果父节点的平衡因子更新为1/-1，说明所在树高度发生变化；
  3. 如果父节点的平衡因子更新为2/-2，说明子树已经不平衡，需要旋转处理。
bool Insert(const pair<K, V>& kv)
{
    if (_root == nullptr) 
    {
        _root = new Node(kv);
        return true;
    }

    Node* parent = nullptr;
    Node* curr = _root;

    while (curr) 
    {
        if (curr->_kv.first < kv.first) {
            parent = curr;
            curr = curr->_right;
        }
        else if (curr->_kv.first > kv.first) {
            parent = curr;
            curr = curr->_left;
        }
        else {
            return false;
        }
    }

    curr = new Node(kv);
    if (parent->_kv.first < kv.first)
        parent->_right = curr;
    else
        parent->_left = curr;
    curr->_parent = parent;

    // 控制平衡
    // 1. 更新平衡因子
    // 2. 旋转处理异常平衡因子

    while (parent) // 更新到根
    { 
        // 更新
        if (curr == parent->_left)
            parent->_bf--;
        else if (curr == parent->_right)
            parent->_bf++;
        
        // 检测
        if (parent->_bf == 0) { // 已经平衡，更新结束
            break;
        }
        else if (parent->_bf == 1 || parent->_bf == -1) // 向上更新
        {
            curr = parent;
            parent = parent->_parent;
        }
        else if (parent->_bf == 2 || parent->_bf == -2) // 平衡被打破，开始旋转
        {
            if (parent->_bf == -2 && curr->_bf == -1)
                RotateR(parent);
            else if (parent->_bf == 2 && curr->_bf == 1)
                RotateL(parent);
            else if (parent->_bf == -2 && curr->_bf == 1)
                RotateLR(parent);
            else if (parent->_bf == 2 && curr->_bf == -1)
                RotateRL(parent);
            break;
        }
        else { 
            assert(false); // 树构建出错
        }
    }
    return true;
}

AVL树的旋转

先看如图所示的树结构的抽象图，节点下方的矩形代表多种可能，分别是a，b，c子树，其高度都是h。

在这里插入图片描述

旋转的方式有四种，目的是在搜索树规则下平衡二叉树，平衡的结果就是树的整体高度减1，提高搜索效率。

旋转后树中各节点的平衡因子达到最佳状态，不需要继续向上更新平衡因子。

右单旋

在这里插入图片描述

左树新增节点，高度+1，导致父节点bf=–1，爷节点bf=–2。此时平衡被破坏，就会引发右单旋。

右单旋就是把bf=-2的节点旋转至bf=-1的节点的右子树上。此时，bf=-1的节点是否存在右子树，有两种情况但可以统一处理。

在这里插入图片描述

  1. 先把bf=-1的节点的右子树链接到bf=-2的节点的左边，
  2. 再将bf=-2的节点链接到bf=-1的节点的右边。
  3. 最后bf=-1的节点作当前树的根，和整棵树链接。

在这里插入图片描述

void rotate_r(node* parent)
{
    node* subl = parent->_left;
    node* sublr = subl->_right;

    parent->_left = sublr;
    if (sublr) sublr->_parent = parent;

    node* pparent = parent->_parent;

    subl->_right = parent;
    parent->_parent = subl;

    if (parent == _root)
    {
        _root = subl;
        subl->_parent = nullptr;
    }
    else
    {
        if (pparent->_left == parent)
            pparent->_left = subl;
        else
            pparent->_right = subl;
        subl->_parent = pparent;
    }

    parent->_bf = 0;
    subl->_bf = 0;
}

在这里插入图片描述

左单旋

在这里插入图片描述

左单旋和右单旋正好相反。左单旋就是把bf=2的节点旋转至bf=1的节点的左子树上。

  1. 先把bf=1的节点的左子树链接到bf=2的节点的右边。
  2. 再将bf=2的节点链接到bf=1的节点的左边。
  3. 最后bf=-1的节点作当前树的根，和整棵树链接。

在这里插入图片描述

void rotate_l(node* parent)
{
    node* subr = parent->_right;
    node* subrl = parent->_left;

    parent->_right = subrl;
    if (subrl) subrl->_parent = parent;

    node* pparent = parent->_parent;

    subr->_left = parent;
    parent->_parent = subr;

    if (parent == _root)
        _root = subr;
    else
    {
        if (pparent->_left == parent)
            pparent->_left = subr;
        else
            pparent->_right = subr;
    }
    subr->_parent = pparent;

    parent->_bf = 0;
    subr->_bf = 0;
}

在这里插入图片描述

左右双旋

左单旋右单旋分别是左高左旋和右高右旋。

左右双旋的情况如下图所示，对于下半部分来说左边高，对于上半部分来说右边高。

在这里插入图片描述

在这里插入图片描述

  1. 先以bf=1的节点为轴进行左单旋；
  2. 再以bf=-2的节点为轴进行右单旋。
void RotateLR(Node* parent) { // 双旋就是由两个单旋组成
    RotateL(parent->_left);
    RotateR(parent);
    //...
}
更新平衡因子

两个单旋会把节点的平衡因子都变成0，显然是不正确的。根据插入节点的位置不同，左右双旋的平衡因子更新有三种情况：

可以通过subLR节点的平衡因子的值来判断三种情况。不管树有多高，我们只在乎新节点在subLR的左右。

插入情况如何判断结果
subLR本身就是新节点subLR.bf=0parent.bf=0,subL.bf=0,subLR.bf=0
新节点在subLR的左边subLR.bf=-1parent.bf=0,subL.bf=-1,subLR.bf=0
新节点在subLR的右边subLR.bf=1parent.bf=1,subL.bf=0,subLR.bf=0
void rotate_lr(node* parent)
{
    node* subl = parent->_left;
    node* sublr = subl->_right;

    int bf = sublr->_bf; // 记录sublr的平衡因子用以判断

    rotate_l(parent->_left);
    rotate_r(parent);

    if (bf == 0) // sublr就是新节点
    {
        parent->_bf = 0;
        subl->_bf = 0;
        sublr->_bf = 0;
    }
    else if (bf == 1) // 插入在sublr的左边
    {
        parent->_bf = 0;
        subl->_bf = -1;
        sublr->_bf = 0;
    }
    else if (bf == -1) // 插入在sublr的右边
    {
        parent->_bf = 1;
        subl->_bf = 0;
        sublr->_bf = 0;
    }
    else
    {
        assert(false);
    }
}

右左双旋

右左双旋和左右双旋正好相反，对于下半部分来说右边高，对于上半部分来说是左边高。

  1. 先以bf=-1的节点为轴进行右单旋；
  2. 再以bf=2的节点为轴进行左单旋。

在这里插入图片描述

在这里插入图片描述

更新平衡因子

右左双旋同样存在如下三种情况：

插入情况如何判断结果
subRL本身就是新节点subRL.bf=0parent.bf=0,subR.bf=0,subRL.bf=0
新节点在subRL的左边subRL.bf=-1parent.bf=0,subR.bf=1,subRL.bf=0
新节点在subRL的右边subRL.bf=1parent.bf=-1,subR.bf=0,subRL.bf=0

在这里插入图片描述

void rotate_rl(node* parent)
{
    node* subr = parent->_right;
    node* subrl = subr->_left;

    int bf = subrl->_bf;

    rotate_r(parent->_right);
    rotate_l(parent);

    if (bf == 0)
    {
        parent->_bf = 0;
        subr->_bf = 0;
        subrl->_bf = 0;
    }
    else if (bf == -1)
    {
        parent->_bf = 0;
        subr->_bf = 1;
        subrl->_bf = 0;
    }
    else if (bf == 1)
    {
        parent->_bf = -1;
        subr->_bf = 0;
        subrl->_bf = 0;
    }
    else
    {
        assert(false);
    }
}

AVL树的验证

void inorder()
{
    _inorder(_root);
    cout << endl;
}
void _inorder(node* root)
{
    if (!root) return;

    _inorder(root->_left);
    cout << root->_kv.first << ":" << root->_kv.second << " ";
    _inorder(root->_right);
}

bool is_balance()
{
    return _is_balance(_root);
}
bool _is_balance(node* root)
{
    if (!root)
        return true;

    int lh  = height(root->_left);
    int rh = height(root->_right);

    if (rh - lh != root->_bf)
    {
        cout << root->_kv.first << "  but now:" << root->_bf << endl;
        cout << root->_kv.first << "should be:" << rh - lh << endl;
        return false;
    }

    return abs(rh - lh) < 2
        && _is_balance(root->_left) && _is_balance(root->_right);
}

int height(node* root)
{
    if (!root)
        return 0;

    int lh = height(root->_left);
    int rh = height(root->_right);

    return rh > lh ? rh + 1 : lh + 1;
}

AVL树、红黑树、B树都是了解性的数据结构，到此足矣。

 

2.2 红黑树

红黑树的定义

红黑树也是一种二叉搜索树，每个结点上都带有红或黑两种颜色。

通过限制整条从根到叶路径上的结点的着色方式，确保整棵树中最长路径的长度不超过最短路径的两倍，因而是接近平衡的。

在这里插入图片描述

红黑树的性质

  1. 每个结点不是红色就是黑色。
  2. 根节点是黑色的。
  3. 红色节点的子结点必须都是黑色的。（不能出现连续的红色节点）
  4. 每条路径所含的黑色结点数量相等。
  5. 每个空结点都是黑色的，空节点也认为是叶结点。
  6. 对于红黑树，我们认为从根到空算一条路径。

搜索效率推导

从红黑树的性质看，最短路径肯定全是黑色节点，最长路径肯定是黑红相间的。

假设黑节点数量为 X X X，则路径的长度满足 X ≤ p a t h _ l e n g t h ≤ 2 X X≤path\_length≤2X X≤path_length≤2X，即红黑树的高度满足 X ≤ h ≤ 2 X X≤h≤2X X≤h≤2X。

首先完全二叉树的高度和节点数量的关系是 2 h − 1 = N 2^h-1=N 2h−1=N。推导到红黑树的节点个数满足：
2 X − 1 ≤ N ≤ 2 2 X − 1 = > 1 2 × l o g 2 N ≤ X ≤ l o g 2 N = > l o g 4 N ≤ X ≤ l o g 2 N 2^{X}-1≤N≤2^{2X}-1\\ => \frac{1}{2}×log_2N≤X≤log_2N \quad => \quad log_4N≤X≤log_2N 2X−1≤N≤22X−1=>21​×log2​N≤X≤log2​N=>log4​N≤X≤log2​N

红黑树的搜索效率为 l o g N ≤ O ( N ) ≤ 2 l o g N logN≤O(N)≤2logN logN≤O(N)≤2logN。

红黑树是接近平衡，AVL树是严格平衡。但CPU的速度快，二者差距不明显，且维护AVL树结构更花时间，所以红黑树应用更多。

红黑树的结构

enum COLOR {
    RED,
    BLACK
};

template <class K, class V>
struct rbtree_node {
    rbtree_node* _left;
    rbtree_node* _right;
    rbtree_node* _parent;
    pair<K, V> _kv;
    COLOR _col;
};

template <class K, class V> 
class rb_tree {
    rbtree_node<K, V>* _root;
    // ...
};

红黑树的插入

红黑树也是搜索二叉树，插入的步骤都是一样的，不同的是维护插入后树的结构。

由于红黑树的性质，每条路径的黑节点数量必须相同，故新插入节点统一采用红色，对整个树的影响最小。

bool insert(const pair<K, V> kv)
{
    if (_root == nullptr) {
        _root = new Node(kv);
		cur->_col = BLACK;
        return true;
    }

    node* parent = nullptr;
    node* cur = _root;

    while (cur) {
        if (cur->_kv.first < kv.first) {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_kv.first > kv.first) {
            parent = cur;
            cur = cur->_left;
        }
        else {
            return false;
        }
    }

    cur = new Node(kv);
    if (parent->_kv.first < kv.first)
        parent->_right = cur;
    else
        parent->_left = cur;
    cur->_parent = parent;

    // 控制平衡
    // ...
}

处理红黑树我们需要确认三个节点：插入新节点 c u r cur cur、父节点 p p p、叔节点 u u u、爷节点 g g g。

插入后，如果父节点是黑节点，则无需处理。只有当父节点是红节点时，就出现了连续红节点，需要处理：

情况解决方案
p为红，g为黑，u为红变色
p为红，g为黑，u为黑或不存在旋转+变色

变色情况

p为红，g为黑，u为红

  • 将父节点叔节点变黑，爷节点变红。
  • cur指向爷节点，继续向上遍历。直到父节点为空或条件不满足。

在这里插入图片描述

if (grandpa->_left == parent) // 父在左
{
    Node* uncle = grandpa->_right;

    /* 情况一：u存在且为红 */
    if (uncle && uncle->_col == RED) // 叔节点存在且为红
    {
        // 变色
        parent->_col = uncle->_col = BLACK;
        grandpa->_col = RED;

        // 向上调整
        curr = grandpa; // 越过父节点直接跳到爷节点
        parent = grandpa->_parent;
    }
    //...
}
else // 父在右
{
    Node* uncle = grandpa->_left;

    /* 情况一：u存在且为红 */
    if (uncle && uncle->_col == RED) // 叔节点存在且为红
    {
        // 变色
        parent->_col = uncle->_col = BLACK;
        grandpa->_col = RED;

        // 向上调整
        curr = grandpa; // 越过父节点直接跳到爷节点
        parent = grandpa->_parent;
    }
    //...
}

旋转情况

p为红，g为黑，u为黑或不存在。

此时我们根据爷父子三个节点呈现出的“形状”而选择旋转方式。

情况旋转方案
子是父的左，父是爷的左右单旋
子是父的右，父是爷的右左单旋
子是父的右，父是爷的左左右双旋
子是父的左，父是爷的右右左双旋

旋转后需要改色，上面的一个改为黑色，下面的两个改红色。

在这里插入图片描述

if (grandpa->_left == parent)
{
    node* uncle = grandpa->_right;

    if (uncle && uncle->_col == RED)
    {}
    else
    {
        if (parent->_left == cur)
        {
            rotate_r(grandpa);
            cur->_col = grandpa->_col = RED;
            parent->_col = BLACK;
        }
        else
        {
            rotate_l(parent);
            rotate_r(grandpa);
            grandpa->_col = parent->_col = RED;
            cur->_col = BLACK;
        }
        break;
    }
}
else
{
    node* uncle = grandpa->_left;

    if (uncle && uncle->_col == RED)
    {}
    else
    {
        if (parent->_left == cur)
        {
            rotate_r(parent);
            rotate_l(grandpa);
            grandpa->_col = parent->_col = RED;
            cur->_col = BLACK;
        }
        else
        {
            rotate_l(grandpa);
            cur->_col = grandpa->_col = RED;
            parent->_col = BLACK;
        }
        break;
    }
}

代码实现

bool insert(const pair<K, V>& kv)
{
    if (!_root)
    {
        _root = new node(kv);
        _root->_col = BLACK;
        return true;
    }

    node* parent = nullptr;
    node* cur = _root;

    while (cur)
    {
        if (cur->_kv.first < kv.first)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_kv.first > kv.first)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            return false;
        }
    }

    cur = new node(kv);
    if (parent->_kv.first < kv.first)
        parent->_right = cur;
    else
        parent->_left = cur;
    cur->_parent = parent;

    while (parent && parent->_col == RED)
    {
        node* grandpa = parent->_parent;

        if (grandpa->_left == parent)
        {
            node* uncle = grandpa->_right;

            if (uncle && uncle->_col == RED)
            {
                parent->_col = uncle->_col = BLACK;
                grandpa->_col = RED;

                cur = grandpa;
                parent = cur->_parent;
            }
            else
            {
                if (parent->_left == cur)
                {
                    rotate_r(grandpa);
                    cur->_col = grandpa->_col = RED;
                    parent->_col = BLACK;
                }
                else
                {
                    rotate_l(parent);
                    rotate_r(grandpa);
                    grandpa->_col = parent->_col = RED;
                    cur->_col = BLACK;
                }
                break;
            }
        }
        else
        {
            node* uncle = grandpa->_left;

            if (uncle && uncle->_col == RED)
            {
                parent->_col = uncle->_col = BLACK;
                grandpa->_col = RED;

                cur = grandpa;
                parent = cur->_parent;
            }
            else
            {
                if (parent->_left == cur)
                {
                    rotate_r(parent);
                    rotate_l(grandpa);
                    grandpa->_col = parent->_col = RED;
                    cur->_col = BLACK;
                }
                else
                {
                    rotate_l(grandpa);
                    cur->_col = grandpa->_col = RED;
                    parent->_col = BLACK;
                }
                break;
            }
        }
    }

    _root->_col = BLACK;
    return true;
}

private:
void rotate_l(node* parent)
{
    node* subr = parent->_right;
    node* subrl = subr->_left;

    parent->_right = subrl;
    if (subrl) subrl->_parent = parent;

    node* pparent = parent->_parent;

    subr->_left = parent;
    parent->_parent = subr;

    if (parent == _root)
        _root = subr;
    else
    {
        if (pparent->_left == parent)
            pparent->_left = subr;
        else
            pparent->_right = subr;
    }
    subr->_parent = pparent;
}

void rotate_r(node* parent)
{
    node* subl = parent->_left;
    node* sublr = subl->_right;

    parent->_left = sublr;
    if (sublr) sublr->_parent = parent;

    node* pparent = parent->_parent;

    subl->_right = parent;
    parent->_parent = subl;

    if (parent == _root)
    {
        _root = subl;
        subl->_parent = nullptr;
    }
    else
    {
        if (pparent->_left == parent)
            pparent->_left = subl;
        else
            pparent->_right = subl;
        subl->_parent = pparent;
    }
}

在这里插入图片描述

红黑树的验证

bool is_rbtree()
{
    if (_root && _root->_col == RED)
        return false;

    int mark = -1;
    return check(_root, mark, 0);
}

bool check(node* root, int& mark, int cnt)
{
    if (!root)
    {
        if (mark == -1)
            mark = cnt;
        else if (mark != cnt)
        {
            cout << "block nodes count error\n" << endl;
            return false;
        }
        return true;
    }

    if (root->_col == BLACK)
        cnt++;

    if (root->_col == RED && root->_parent->_col == RED)
    {
        cout << "consecutive red nodes "
             << root->_parent->_kv.first << " and "
             << root->_kv.first << endl;
        return false;
    }

    return check(root->_left, mark, cnt) && check(root->_right, mark, cnt);
}

红黑树

 

3. 实现封装

map和set如何复用同一棵红黑树呢？

在这里插入图片描述

3.1 整体设计

template <class Key, class T, class Compare = less<Key>, class Alloc = alloc>
class map {
    typedef Key key_type;
    typedef pair<const Key, T> value_type;
    typedef rb_tree<key_type, value_type, 
                      select1st<value_type>, key_compare, Alloc> rep_type;
    rep_type t;
}

template <class Key, class Compare = less<Key>, class Alloc = alloc>
class set {
    typedef Key key_type;
    typedef Key value_type;
    typedef rb_tree<key_type, value_type, 
                  identity<value_type>, key_compare, Alloc> rep_type;
    rep_type t;  
}

template <class Key, class Value, class KeyOfValue, class Compare, class Alloc = alloc>
class rb_tree {
	typedef __rb_tree_node<Value> rb_tree_node;
}

template <class Value>
struct __rb_tree_node {
	Value value_field;
};

set<K>    -> rb_tree<K, K>                 -> rb_tree_node<K>
map<K, V> -> rb_tree<K, pair<const K, V> > -> rb_tree_node<pair<const K, V> >
模版参数作用
Key可以直接拿到Key类型，编译模版的时候需要确定Key类型
Value决定了树节点元素存储的数据的类型
KeyOfValue仿函数，用来获取Value中的Key值，如果是map就是取kv.first如果是set就是K
Compare仿函数，Key类型的比较函数
template<class V>
struct rbt_node
{};
template<class K, class V, class KeyOfValue, class Compare>
class rb_tree
{};

template<class K, class CmpOfKey = less<K>>
class set
{
    bool insert(const K& key) { t.insert(key); }
    class KeyOfVal { K& operator()(const K& key) { return key; } };
    rb_tree<K, K, KeyOfVal, CmpOfKey> t;
};

template<class K, class V, class CmpOfKey = less<K>>
class map
{
    bool insert(const pair<const K, V>& kv) { t.insert(kv); }
    class KeyOfVal { K& operator()(const pair<const K, V>& kv) { return kv.first; } };
    rb_tree<K, pair<const K, V>, KeyOfVal, CmpOfKey> t;
};

3.2 红黑树

默认函数

template<class V>
struct rbt_node
{
    rbt_node<V>* _left;
    rbt_node<V>* _right;
    rbt_node<V>* _parent;

    V _val;
    COLOR _col;

    rbt_node<V>(const V& val)
        : _left(nullptr), _right(nullptr), _parent(nullptr)
        , _val(val), _col(RED)
    {}
};

template<class K, class V, class KeyOfValue, class Compare>
class rb_tree
{
public:
    typedef rbt_node<V> node;

public:
    rb_tree()
    {}

    rb_tree(const rb_tree& t)
    {
        _root = copy(_root);
    }

    rb_tree& operator=(const rb_tree t)
    {
        if (this != &t)
        {
            swap(_root, t._root);
        }
        return *this;
    }

    ~rb_tree()
    {
        destroy(_root);
        _root = nullptr;
    }

private:
    node* copy(node* root)
    {
        if (!root)
            return nullptr;

        node* new_node = new node(root->_kv);
        new_node->_left = copy(root->_left);
        new_node->_right = copy(root->_right);
        return new_node;
    }

    void destroy(node* root)
    {
        if (!root)
            return;

        destroy(root->_left);
        destroy(root->_right);
        delete root;
    }
    
    bool insert(const V& val)
    {
        // ...
        if (_kov(cur->_val) < _kov(val))
        else if (_kov(cur->_val) > _kov(val))
        // ...
    }

private:
    KeyOfValue _kov;
    Compare _cmp;
    node* _root = nullptr;
};

插入函数

pair<iterator, bool> insert(const V& val)
{
    if (!_root)
    {
        _root = new node(val);
        _root->_col = BLACK;
        return {iterator(_root), true};
    }

    node* parent = nullptr;
    node* cur = _root;

    while (cur)
    {
        if (_cmp(_kov(cur->_val), _kov(val)))
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (_cmp(_kov(val), _kov(cur->_val)))
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            return {iterator(cur), false};
        }
    }

    cur = new node(val);
    if (_cmp(_kov(parent->_val), _kov(val)))
        parent->_right = cur;
    else
        parent->_left = cur;
    cur->_parent = parent;

    while (parent && parent->_col == RED)
    {
        node* grandpa = parent->_parent;

        if (grandpa->_left == parent)
        {
            node* uncle = grandpa->_right;

            if (uncle && uncle->_col == RED)
            {
                parent->_col = uncle->_col = BLACK;
                grandpa->_col = RED;

                cur = grandpa;
                parent = cur->_parent;
            }
            else
            {
                if (parent->_left == cur)
                {
                    rotate_r(grandpa);
                    cur->_col = grandpa->_col = RED;
                    parent->_col = BLACK;
                }
                else
                {
                    rotate_l(parent);
                    rotate_r(grandpa);
                    grandpa->_col = parent->_col = RED;
                    cur->_col = BLACK;
                }
                break;
            }
        }
        else
        {
            node* uncle = grandpa->_left;

            if (uncle && uncle->_col == RED)
            {
                parent->_col = uncle->_col = BLACK;
                grandpa->_col = RED;

                cur = grandpa;
                parent = cur->_parent;
            }
            else
            {
                if (parent->_left == cur)
                {
                    rotate_r(parent);
                    rotate_l(grandpa);
                    grandpa->_col = parent->_col = RED;
                    cur->_col = BLACK;
                }
                else
                {
                    rotate_l(grandpa);
                    cur->_col = grandpa->_col = RED;
                    parent->_col = BLACK;
                }
                break;
            }
        }
    }

    _root->_col = BLACK;
    return {iterator(cur), true};
}

迭代器

template<class V, class Ref, class Ptr>
struct __rb_tree_iterator
{
    typedef __rb_tree_node<V> node;
    typedef __rb_tree_iterator<V, Ref, Ptr> self;
    
    node* _node = nullptr;

    __rb_tree_iterator<V, Ref, Ptr>(node* node)
        : _node(node)
    {}
    
    // support normal iter construt const iter
    __rb_tree_iterator(const __rb_tree_iterator<V, V&, V*>& it)
        : _node(it.node)
    {}

    Ref operator*()
    {
        return _node->_val;
    }
    Ptr operator->()
    {
        return &_node->_val;
    }

    bool operator==(const self& s)
    {
        return _node == s._node;
    }
    bool operator!=(const self& s)
    {
        return _node != s._node;
    }
};

库中是将根节点带个头节点，头节点的左孩子指向整个树的最左节点，右孩子指向整个树的最右节点；

在这里插入图片描述

  • 如果节点的右子树不为空，下一个位置就是节点的右子树的最左节点。
  • 如果节点的右子树为空，向上遍历，找到某个节点，满足该节点是其父亲的左，该父亲就是下一个位置。
self& operator++()
{
    if (_node->_right)
    {
        node* left = _node->_right;
        while (left->_left)
        {
            left = left->_left;
        }
        _node = left;
    }
    else
    {
        node* cur = _node;
        node* parent = cur->_parent;

        while (parent && parent->_right == cur)
        {
            cur = parent;
            parent = cur->_parent;
        }
        _node = parent;
    }
    return *this;
}

self& operator--()
{
    if (!_node) assert(false); // can't do that

    if (_node->_left)
    {
        node* right = _node->_left;
        while (right->_right)
        {
            right = right->_right;
        }
        _node = right;
    }
    else
    {
        node* cur = _node;
        node* parent = cur->_parent;

        while (parent && parent->_left == cur)
        {
            cur = parent;
            parent = cur->_parent;
        }
        _node = parent;
    }
    return *this;
}

在这里插入图片描述

3.3 set

template<class K, class Compare = less<K>>
class set
{
private:
    struct KeyOfVal {
        const K& operator()(const K& key) { return key; }
    };

public:
    typedef rb_tree<K, K, KeyOfVal, Compare> rep_type;
    typedef typename rep_type::const_iterator iterator; // use const iter
    typedef typename rep_type::const_iterator const_iterator;

public:
    pair<iterator, bool> insert(const K& key) { return _t.insert(key); }
    iterator find(const K& key) { return _t.find(key); }
    void inorder() { _t.inorder(); }

public:
    iterator begin() { return _t.begin(); }
    iterator end() { return _t.end(); }

private:
    rb_tree<K, K, KeyOfVal, Compare> _t;
};

3.4 map

template<class K, class V, class Compare = less<K>>
class map
{
private:
    struct KeyOfVal {
        const K& operator()(const pair<const K, V>& kv) { return kv.first; }
    };

public:
    typedef rb_tree<K, pair<const K, V>, KeyOfVal, Compare> rep_type;
    typedef typename rep_type::iterator iterator;
    typedef typename rep_type::const_iterator const_iterator;

public:
    iterator find(const K& key) { return _t.find(key); }
    pair<iterator, bool> insert(const pair<const K, V>& kv) { return _t.insert(kv); }
    V& operator[](const K& key) { return _t.insert(make_pair(key, V())).first->second; }
    void inorder() { _t.inorder(); }

    iterator begin() { return _t.begin(); }
    iterator end() { return _t.end(); }

private:
    rep_type _t;
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/760401.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

NOSQL简单实战

NOSQL简单实战

目录 实战一&#xff1a; 1、 string类型数据的命令操作&#xff1a; &#xff08;1&#xff09; 设置键值&#xff1a; &#xff08;2&#xff09; 读取键值&#xff1a; &#xff08;3&#xff09; 数值类型自增1&#xff1a; &#xff08;4&#xff09; 数值类型自减1&…
阅读更多...
基于html2canvas和jspdf将document DOM节点转换为图片生成PDF文件，并下载到本地

基于html2canvas和jspdf将document DOM节点转换为图片生成PDF文件，并下载到本地

这里要用到html2canvas将document DOM节点转换为图片&#xff0c;并下载到本地_你挚爱的强哥的博客-CSDN博客前端用原生js编辑文件内容→创建生成文件(格式可以自定义)→下载文件_你挚爱的强哥的博客-CSDN博客。会自动创建一个html文件。https://blog.csdn.net/qq_37860634/art…
阅读更多...
业务中添加历史版本事务并发处理

业务中添加历史版本事务并发处理

业务背景&#xff1a;项目中包含历史版本的管理&#xff0c;每次保存历史版本都添加一条新的记录到数据库&#xff0c;且版本号加1。保存版本的时候1.要先查询历史版本数据表&#xff0c;获取当前最新的版本号&#xff1b;2.最新的版本号加1&#xff0c;插入数据历史版本记录表…
阅读更多...
dp算法 力扣174地下城游戏

dp算法 力扣174地下城游戏

在学习编程时&#xff0c;算法是一道硬菜&#xff0c;而dp作为算法的一份子&#xff0c;它的地位在编程界举足轻重。 174. 地下城游戏 - 力扣&#xff08;LeetCode&#xff09; 本文是Java代码哦~ 一、题目详情 恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地…
阅读更多...
Vue列表渲染（v-for）以及key的作用与原理

Vue列表渲染（v-for）以及key的作用与原理

索引值的两种写法&#xff1a; <!--index遍历时的默认索引值--> <ul><li v-for"(p,index) in persons":key"index">{{p.name}}--{{p.age}}</li></ul> 代码&#xff1a; v-for"p in persons" :key"p.id&quo…
阅读更多...
【多维数组对象拍平处理为一维数组】

【多维数组对象拍平处理为一维数组】

这里写自定义目录标题 欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题&#xff0c;有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants 创建一个自定义列表如何创建一个…
阅读更多...
深谋远“绿”，数据中心未来之路在何方？

深谋远“绿”，数据中心未来之路在何方？

数据中心未来演进方向是什么&#xff1f; 在中国绿色算力大会-华为数据中心平行会议上&#xff0c;业界愈发形成共识&#xff1a;即在双碳目标的大背景下&#xff0c;数据中心走向绿色低碳化、智能化。 去年初&#xff0c;东数西算工程正式启动建设&#xff0c;标志着我国数据…
阅读更多...
Ui自动化测试上传文件方法都在这里了

Ui自动化测试上传文件方法都在这里了

目录 前言 被测HTML代码 send_keys方法 实例------------------------------------ Time : 2019/7/17 19:03 Auth : linux超 File : upload_file_send_keys.py IDE : PyCharm Motto: Real warriors,dare to face the bleak warning,dare to face the incisive error! QQ : 2…
阅读更多...
代码随想录第26天 | ● 332.重新安排行程 ● 51. N皇后 ● 37. 解数独

代码随想录第26天 | ● 332.重新安排行程 ● 51. N皇后 ● 37. 解数独

332. 重新安排行程 /*** param {string[][]} tickets* return {string[]}*/var findItinerary function (tickets) {let s "ZZZ";let start;for (let i in tickets) {if (tickets[i][0] "JFK" && tickets[i][1] < s) {start i;s tickets[i…
阅读更多...
密码学学习笔记(十三)：哈希函数 - Merkle–Damgård结构

密码学学习笔记(十三)：哈希函数 - Merkle–Damgård结构

Merkle–Damgrd是一种算法&#xff0c;由Ralph Merkle和Ivan Damgrd提出。它通过迭代调用压缩函数来计算消息的哈希值。 应用 拿SHA-2举例&#xff0c;首先我们需要对需要进行哈希运算的输入做填充&#xff0c;然后将填充后的输入划分为等长的分组&#xff0c;每个分组的长度…
阅读更多...
uniapp 土法 瀑布流 - vue3

uniapp 土法 瀑布流 - vue3

效果图 代码 <template><view><!-- 瀑布流展示 --><!-- 标签页 --><view class="rowStart flexNoLineBreaking paddingCol10 innerDomPaddingRow5 tinyShadow marginBottom10"><view @click="tabsCurrent = 0; run_waterfa…
阅读更多...
计算机网络基础第六章

计算机网络基础第六章

一、应用层概述 1.1 网络应用模型 1.1.1 客户/服务器(C/S)模型 1.1.2 P2P模型 二、域名解析系统——DNS系统 2.1 域名 2.2 域名服务器 2.3 域名解析过程 三、文件传输协议——FTP 3.1 FTP服务器和用户端 3.2 FTP工作原理 四、电子邮件 4.1 电子邮件系统概述 4.2 简单邮件传送…
阅读更多...
C# Modbus通信从入门到精通（1）——Modbus RTU（虚拟串口调试工具的使用）

C# Modbus通信从入门到精通（1）——Modbus RTU（虚拟串口调试工具的使用）

前言： 订阅本专栏后，加入vip专属的qq群，在群资料里面就能找到虚拟串口工具 1、安装虚拟串口工具 第1步、双击vspd.exe安装 第2步、 打开“Cracked”的文件夹，里面有一个vspdct.dll，如下图：把这个dll粘贴到C:\Program Files (x86)\Eltima Software\Virtual Serial Po…
阅读更多...
Python垃圾回收

Python垃圾回收

Python垃圾回收 文章目录 Python垃圾回收引用计数标记清除分代回收 GC作为现代编程语言的自动内存管理机制&#xff0c;专注于两件事&#xff1a; 找到内存中无用的垃圾资源清除这些垃圾并把内存让出来给其他对象使用。 GC彻底把程序员从资源管理的重担中解放出来&#xff0c;让…
阅读更多...
MySQL-DML-添加数据insert

MySQL-DML-添加数据insert

目录 添加数据&#xff1a;insert insert语法 注意事项 修改数据&#xff1a;update update语法 注意事项&#xff1a; 删除数据&#xff1a;delete 删除语法 注意事项 总结 DML英文全称Data Manipulation Language&#xff08;数据操作语言&#xff09;&#xff0c;…
阅读更多...
数据结构---B+Tree

数据结构---B+Tree

文章目录 BTree简单了解一下BTree MySQL表数据文件MyISAM存储引擎和InnoDB存储引擎的区别&#xff1f; BTree 在我没了解BTree之前&#xff0c;听别人提到这个词时&#xff0c;脑子一片空白&#xff0c;懵懵的&#xff0c;今天利用空闲时间&#xff0c;简单了解了一下BTree&am…
阅读更多...
去掉浮夸，空杯心态重新面对测试

去掉浮夸，空杯心态重新面对测试

刚开始一头扎进软件测试行业&#xff0c;从踏踏实实的机械化功能测试&#xff0c;到学会和甲方扯皮&#xff0c;到被鄙视的五体投地后抓紧修炼表面功夫来忽悠人&#xff0c;学的最多的反而是怎么与人交流。第一次面对跳槽的机会&#xff0c;我竟然发现自己的测试能力不升反降。…
阅读更多...
微服务系统面经

微服务系统面经

微服务架构 秒杀微服务架构图 项目地址可以参考&#xff1a;秒杀系统 1 一个java的微服务系统中有几个网关&#xff1f; 在一个Java的微服务系统中&#xff0c;网关的数量并不固定&#xff0c;这完全取决于系统的设计和需求。网关服务是微服务架构中的重要组件&#xff0c;它…
阅读更多...
架构训练营学习笔记：4-4如何设计存储架构？

架构训练营学习笔记：4-4如何设计存储架构？

存储架构设计的三个步骤 分为&#xff1a;1 估算性能需求 2、选择存储系统 3 设计存储方案 性能估算步骤 一 用户量预估 2B的业务&#xff0c;数据量需要预估&#xff0c;2C的需要决策。 方法&#xff1a; 规划&#xff1a;根据成本、预算、目标等确定 推算&#xff1a;基于…
阅读更多...
SRA数据下载的一个坑

SRA数据下载的一个坑

前两天协助处理GEO数据上的一个单细胞数据&#xff0c;发现了一个巨坑&#xff0c;这里分享下&#xff0c;希望大家能避开。 需要下载的数据集是&#xff0c;GSE119562&#xff0c;查询SRA Run Selector&#xff0c;找到它对应的SRR编号。 于是&#xff0c;我非常熟练的用pref…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023