树中距离之和

力扣链接：834. 树中距离之和

题目描述

给定一个无向、连通的树。树中有 n 个标记为 0…n-1 的节点以及 n-1 条边 。

给定整数 n 和数组 edges ， edges[i] = [ai, bi]表示树中的节点 ai 和 bi 之间有一条边。

返回长度为 n 的数组 answer ，其中 answer[i] 是树中第 i 个节点与所有其他节点之间的距离之和。

示例

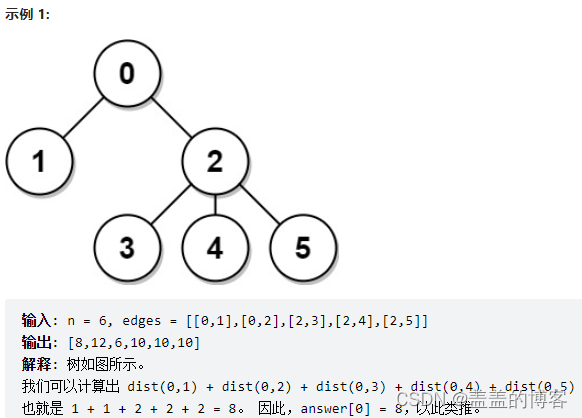
解题思路

定义 dp[u] 表示以 u 为根的子树，它的所有子节点到它的距离之和，同时定义 sz[u] 表示以 u 为根的子树的节点数量。进行换根操作，维护dp值。

Java代码

class Solution {
    int[] ans;
    int[] sz;
    int[] dp;
    List<List<Integer>> graph;

    public int[] sumOfDistancesInTree(int n, int[][] edges) {
        ans = new int[n];
        sz = new int[n];
        dp = new int[n];
        graph = new ArrayList<List<Integer>>();
        for (int i = 0; i < n; ++i) {
            graph.add(new ArrayList<Integer>());
        }
        for (int[] edge: edges) {
            int u = edge[0], v = edge[1];
            graph.get(u).add(v);
            graph.get(v).add(u);
        }
        dfs(0, -1);
        dfs2(0, -1);
        return ans;
    }

    public void dfs(int u, int f) {
        sz[u] = 1;
        dp[u] = 0;
        for (int v: graph.get(u)) {
            if (v == f) {
                continue;
            }
            dfs(v, u);
            dp[u] += dp[v] + sz[v];
            sz[u] += sz[v];
        }
    }

    public void dfs2(int u, int f) {
        ans[u] = dp[u];
        for (int v: graph.get(u)) {
            if (v == f) {
                continue;
            }
            int pu = dp[u], pv = dp[v];
            int su = sz[u], sv = sz[v];

            dp[u] -= dp[v] + sz[v];
            sz[u] -= sz[v];
            dp[v] += dp[u] + sz[u];
            sz[v] += sz[u];

            dfs2(v, u);

            dp[u] = pu;
            dp[v] = pv;
            sz[u] = su;
            sz[v] = sv;
        }
    }
}

---

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/sum-of-distances-in-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。