论文笔记--PTR: Prompt Tuning with Rules for Text Classification
- 1. 文章简介
- 2. 文章概括
- 3 文章重点技术
- 3.1 Pre-training & Fine-tuning & Prompt-based Fine Tuning
- 3.2 PTR(Prompt Tuning with Rules)
- 3.3 task decomposition
- 3.4 Sub-prompts composition
- 3.5 多个label words的情况
- 4. 文章亮点
- 5. 原文传送门
- 6. References
1. 文章简介
- 标题:PTR: Prompt Tuning with Rules for Text Classification
- 作者:Xu Han, Weilin Zhao, Ning Ding, Zhiyuan Liu, Maosong Sun
- 日期:2022
- 期刊:AI Open
2. 文章概括
文章提出了PTR(Prompt Runing with Rules)用于文本多分类任务,核心思想在于将任务分解为子任务,然后根据预先定义的一些sub-prompts组合成新的prompt,从而更好地挖掘模型蕴含的知识。
3 文章重点技术
3.1 Pre-training & Fine-tuning & Prompt-based Fine Tuning
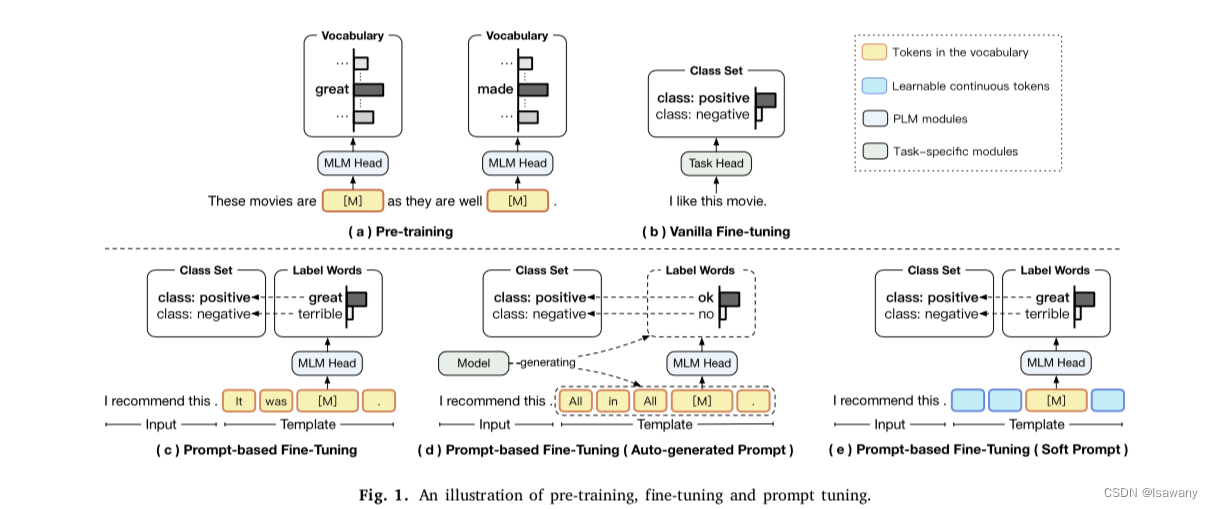
Pre-training一般通过BERT[1]完形填空来达成训练,如下图(a)所示,我们随机掩码一些token,然后再根据上下文预测这些token。
在一些任务中,我们要根据task的特性对模型进行微调,也就是Fine-tuning(FT),如下图(b)所示,FT阶段我们会在下游任务数据上微调模型的参数,从而使得模型在特定任务上表现更好。
但上述预训练和FT由于训练目标(完形填空VS分类/…)的差异会存在gap,为了解决上述gap,我们常用prompt-based FT来进行微调,如下图©所示,我们将标注数据嵌入到prompt中,这样下游任务目标也可以转化为一个完形填空式任务。
但针对关系提取等较为复杂的NLP任务时,上述prompt-based FT很难挑选合适的prompt和label words来支撑推理,此时可以采用auto-generated prompt方法,让模型自己生成prompt,如下图(d)所示。
但上述auto-generated prompt会产生额外的计算,为此我们可以通过Soft Prompt来解决,即下图(e),在hard prompt基础上进行梯度搜索。但soft prompt的问题时模型参数要足够大才会有效。
3.2 PTR(Prompt Tuning with Rules)
为了解决上述问题,文章提出了PTR,可以将单个复杂任务分解为几个简单的子任务,然后设计这些子任务的sub-prompt,再将sub-prompts整合成一个prompt。
具体来说,给定文本分类任务
T
=
{
X
,
Y
}
\mathcal{T}=\{\mathcal{X}, \mathcal{Y}\}
T={X,Y},文章将任务分解为一系列条件函数
F
\mathcal{F}
F。
f
∈
F
f \in \mathcal{F}
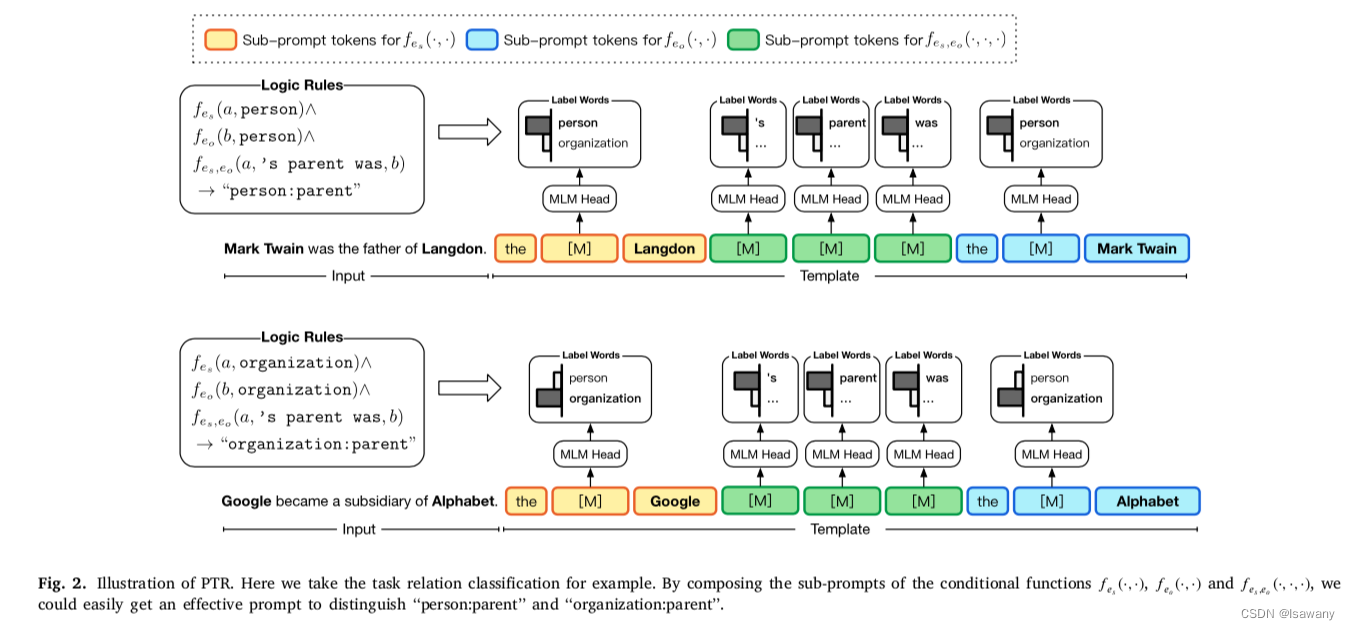
f∈F用于决定单个条件是否满足。如下图第一个例子所示,我们考虑一个关系提取任务"person:parent",给定句子"Mark Twain was the father of Langdon",我们要判定其中实体的关系。为此文章将任务分解为1)
f
e
s
(
⋅
,
⋅
)
f_{e_s}(\cdot, \cdot)
fes(⋅,⋅): "Mark Twain"是一个person 2)
f
e
o
(
⋅
,
⋅
)
f_{e_o}(\cdot, \cdot)
feo(⋅,⋅): “Langdon"是一个person 3)
f
e
s
,
e
o
(
⋅
,
⋅
,
⋅
)
f_{e_s, e_o}(\cdot, \cdot, \cdot)
fes,eo(⋅,⋅,⋅): “Mark Twain"和"Langdon"的关系为”'s Parent was”,写成表达式即为
f
e
s
(
a
,
p
e
r
s
o
n
)
∧
f
e
s
,
e
o
(
a
,
′
s
p
a
r
e
n
t
w
a
s
,
b
)
∧
f
e
o
(
b
,
p
e
r
s
o
n
)
f_{e_s}(a, person) \land f_{e_s, e_o}(a, 's\ parent\ was, b) \land f_{e_o}(b, person)
fes(a,person)∧fes,eo(a,′s parent was,b)∧feo(b,person),其中
e
s
,
e
o
e_s, e_o
es,eo分别代表subject/object实体。
3.3 task decomposition
上述思想中一个关键的技术为如何将任务进行分解。文章利用了各个数据集中的标注信息来得到结构化信息,比如意图分类中,“card_activating”和"card_linking"均包含"card",从而我们可以将任务拆分为"card"部分和后缀部分。根据类似的规则,可以将文本多分类任务表示为层级分类格式,并根据每一层级设计一个条件函数。
对于每个条件函数
f
∈
F
f\in\mathcal{F}
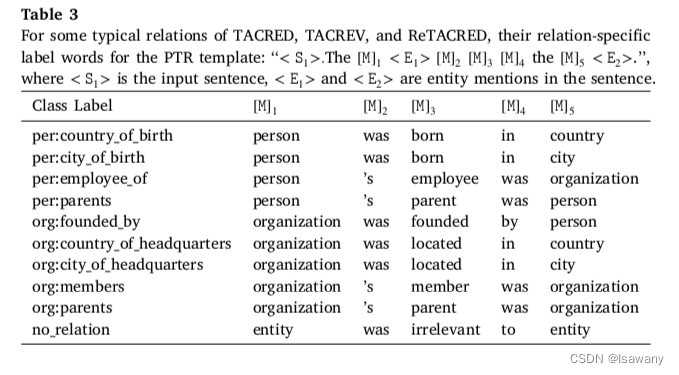
f∈F,文章手动设计一个与之对应的sub-prompt。下表展示了文章针对关系提取任务设计的一些prompt。比如针对类别为"person:country_of_birth",文章设计的prompt为"
<
S
1
>
<S1>
<S1>. The person
<
E
1
>
<E1>
<E1> was born is the country
<
E
2
>
<E2>
<E2>",其中
<
S
1
>
<S1>
<S1>表示原句,
<
E
1
>
,
<
E
2
>
<E1>, <E2>
<E1>,<E2>表示subject/object实体。
3.4 Sub-prompts composition
将子任务分解之后,我们可以得到每个任务对应的sub-prompt,接下来需要将这些sub-prompts进行整合。考虑到
f
e
s
,
e
o
(
a
,
′
s
p
a
r
e
n
t
w
a
s
,
b
)
f_{e_s, e_o}(a, 's\ parent\ was, b)
fes,eo(a,′s parent was,b)的概率可能基于
f
e
s
(
a
,
p
e
r
s
o
n
)
f_{e_s}(a, person)
fes(a,person)和
f
e
o
(
b
,
p
e
r
s
o
n
)
f_{e_o}(b, person)
feo(b,person),文章考虑将所有sub-prompts整合为一个prompt:直接concat所有promp,即
T
(
x
)
=
[
T
f
e
s
(
x
)
;
T
f
e
s
,
e
o
(
x
)
;
T
f
e
o
(
x
)
;
]
=
x
t
h
e
[
M
]
1
e
s
[
M
]
2
[
M
]
3
[
M
]
4
t
h
e
[
M
]
5
e
o
T(x) = [T_{f_{e_s}}(x);T_{f_{e_s, e_o}}(x);T_{f_{e_o}}(x);] \\= x\ the\ [M]_1\ e_s\ [M]_2\ [M]_3 [M]_4\ the\ [M]_5\ e_o
T(x)=[Tfes(x);Tfes,eo(x);Tfeo(x);]=x the [M]1 es [M]2 [M]3[M]4 the [M]5 eo。其中
;
;
;表示sub-prompts之间的聚合操作,对应的联合概率为
p
(
y
∣
x
)
=
∏
j
=
1
n
p
(
[
M
]
j
=
ϕ
j
(
y
)
∣
T
(
x
)
)
∑
y
‾
∈
Y
∏
j
=
1
n
p
(
[
M
]
j
=
ϕ
j
(
y
‾
)
∣
T
(
x
)
)
(1)
p(y|x) = \frac {\prod_{j=1}^n p([M]_j = \phi_j(y) | T(x))}{\sum_{\overline{y}\in\mathcal{Y} \prod_{j=1}^n p([M]_j = \phi_j(\overline{y}) | T(x))}} \tag{1}
p(y∣x)=∑y∈Y∏j=1np([M]j=ϕj(y)∣T(x))∏j=1np([M]j=ϕj(y)∣T(x))(1),其中
n
n
n为template
T
(
x
)
T(x)
T(x)中的掩码个数。推理阶段我们直接采用上式来预测每个mask即可。
在训练阶段,我们会考虑将独立概率和联合概率结合,最终的PTR的损失函数为
L
=
1
∣
X
∣
∑
x
∈
X
(
L
i
n
d
e
p
(
x
)
+
L
j
o
i
n
t
(
x
)
)
=
1
∣
X
∣
∑
x
∈
X
[
−
1
n
∑
j
=
1
n
log
p
(
[
M
]
j
=
ϕ
j
(
y
x
)
∣
T
(
x
)
)
−
log
p
(
y
x
∣
x
)
]
\mathcal{L} = \frac 1{|\mathcal{X}|} \sum_{x\in\mathcal{X}} (\mathcal{L}_{indep}(x) + \mathcal{L}_{joint}(x))\\=\frac 1{|\mathcal{X}|} \sum_{x\in\mathcal{X}} \left[-\frac 1n \sum_{j=1}^n \log p([M]_j = \phi_j (y_x) | T(x)) -\log p(y_x|x)\right]
L=∣X∣1x∈X∑(Lindep(x)+Ljoint(x))=∣X∣1x∈X∑[−n1j=1∑nlogp([M]j=ϕj(yx)∣T(x))−logp(yx∣x)],其中
log
p
(
y
x
∣
x
)
\log p(y_x|x)
logp(yx∣x)由(1)定义。
3.5 多个label words的情况
针对一些场景,同一个y值可能对应多个label words。如情感分类中positive可能对应"great, good"等,此时我们需要调整上面的等于关系为包含关系,特别地我们可以针对每个label words增加权重,最后的概率可表示为 1 m ∑ k = 1 m λ k p ( [ M ] j = w j , k ∣ T ( x ) ) \frac 1m \sum_{k=1}^m \lambda_k p([M]_j = w_{j,k}|T(x)) m1k=1∑mλkp([M]j=wj,k∣T(x)),其中 λ k \lambda_k λk为每个label word的权重,默认为1。
4. 文章亮点
文章提出了PTR,一种可以将复杂NLP任务进行分解,并通过将每个子任务的sub-prompt进行整合得到最终的prompt。文章在关系分类、实体提取和意图分类上进行了数值试验,结果表明,PTR相比于FT方法效果大幅提升,和其它prompt-based FT方法相比也有小幅提升或追平SOTA。文章论证了“预训练模型中包含足够多的下游任务相关知识,我们可以通过增加规则来用合适的prompt引导模型作出正确的推理。”
5. 原文传送门
PTR: Prompt Tuning with Rules for Text Classification
6. References
[1] 论文笔记–BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding