前言

本篇文章会涉及多道位运算题目，由简到难，大家可以跟着练习一下

191. 位1的个数

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数
在这里插入图片描述

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count = 0;
        while(n != 0) {
            if((n & 1) == 1) {
                count++;
            }
            n >>>= 1;
        }
        return count;
    }
}

338. 比特位计数

给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数，返回一个长度为 n + 1 的数组 ans 作为答案。
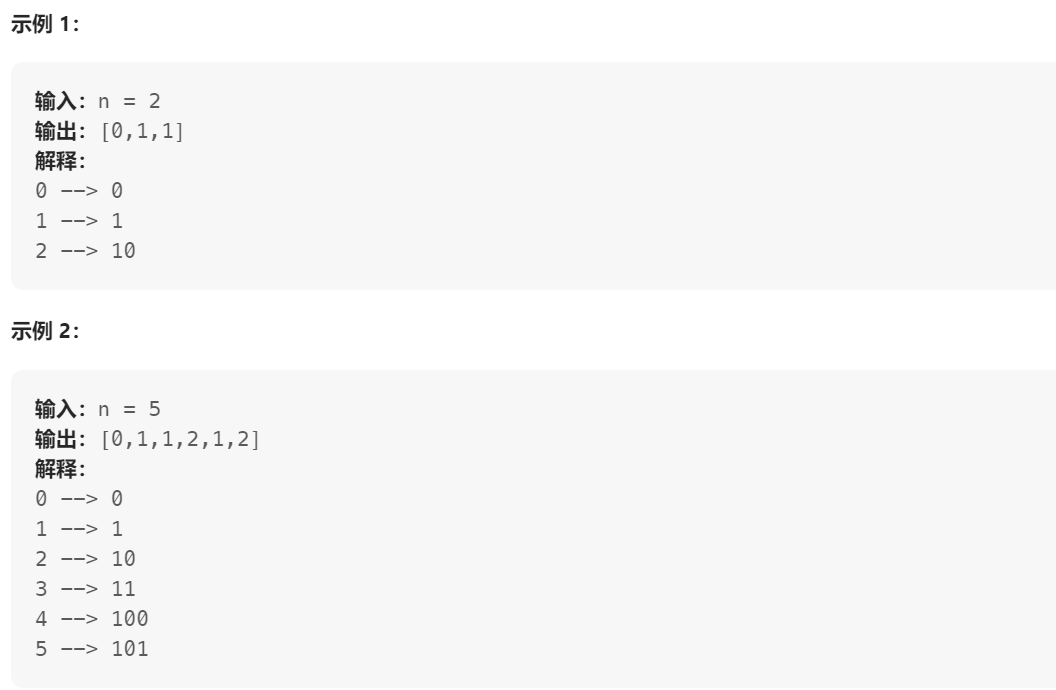
在这里插入图片描述

class Solution {
    public int[] countBits(int n) {
        int[] arr = new int[n + 1];
        for(int i = 0;i < arr.length;i++) {
            arr[i] = count(i);
        }
        return arr;
    }
    public int count(int n) {
        int count = 0;
        while(n != 0) {
            if((n & 1) == 1) {
                count++;
            }
            n >>>= 1;
        }
        return count;
    }
}

461. 汉明距离

两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。

给你两个整数 x 和 y，计算并返回它们之间的汉明距离。
在这里插入图片描述

class Solution {
    public int hammingDistance(int x, int y) {
        int count = 0;
        while(x != 0 || y != 0) {
            if((x & 1) != (y & 1)) {
                count++;
            }
            x >>>= 1;
            y >>>= 1;
        }
        return count;
    }
}

136. 只出现一次的数字

给你一个非空整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

在这里插入图片描述

class Solution {
    public int singleNumber(int[] nums) {
        int ret = 0;
        for(int i = 0;i < nums.length;i++) {
            ret ^= nums[i];
        }
        return ret;
    }
}

260. 只出现一次的数字 III

给你一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。找出只出现一次的那两个元素。你可以按任意顺序返回答案。

你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。
在这里插入图片描述

class Solution {
    public int[] singleNumber(int[] nums) {
        int ret = nums[0];
        for(int i = 1;i < nums.length;i++) {
            ret ^= nums[i];
        }
        int n = (ret & (-ret));
        int[] arr = new int[2];
        for(int i : nums) {
            if((i & n) == n) {
                arr[0] ^= i;
            } else {
                arr[1] ^= i;
            }
        }
        return arr;
    }
}

面试题 01.01. 判定字符是否唯一

实现一个算法，确定一个字符串 s 的所有字符是否全都不同。
这道题的解法有很多，我们这里使用位图解决
在这里插入图片描述

class Solution {
    public boolean isUnique(String astr) {
        if(astr.length() > 26) {
            return false;
        }
        int bitMap = 0;
        for(int i = 0;i < astr.length();i++) {
            int x = astr.charAt(i) - 'a';
            if(((bitMap >> x) & 1) == 1) {
                return false;
            }
            bitMap |= (1 << x);
        }
        return true;
    }
}

268. 丢失的数字

给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数
在这里插入图片描述

class Solution {
    public int missingNumber(int[] nums) {
        int ret = 0;
        for(int i = 0;i < nums.length;i++) {
            ret = ret ^ i ^ nums[i];
        }
        return ret ^ nums.length;
    }
}

371. 两整数之和

给你两个整数 a 和 b ，不使用运算符 + 和 - ，计算并返回两整数之和。
本题借助使用^运算和&运算实现加法
在这里插入图片描述

class Solution {
    public int getSum(int a, int b) {
        while(b != 0) {
            int n = a ^ b;
            b = (a & b) << 1;
            a = n;
        }
        return a;
    }
}

137. 只出现一次的数字 II

给你一个整数数组 nums ，除某个元素仅出现一次外，其余每个元素都恰出现三次。请你找出并返回那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法且不使用额外空间来解决此问题。
本题的解法可以解决不同类型的题目，每个元素出现4.5…n次，出现几次我们%几即可
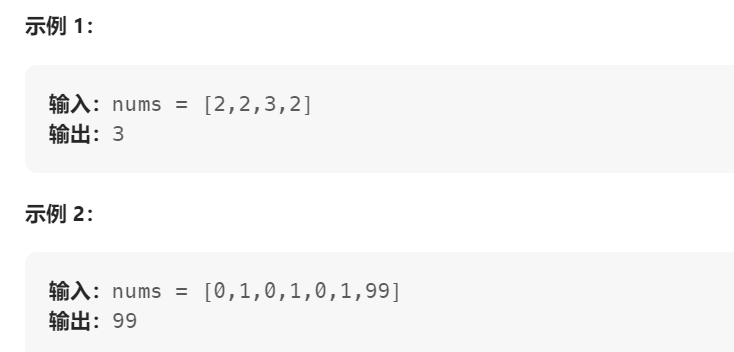
在这里插入图片描述

class Solution {
    public int singleNumber(int[] nums) {
        int ret = 0;
        for(int i = 0;i < 32;i++) {
            int sum = 0;
            for(int x : nums) {
                if(((x >> i) & 1) == 1) {
                    sum++;
                }
            }
            sum %= 3;
            if(sum == 1) {
                ret |= (1 << i);
            }
        }
        return ret;
    }
}

面试题 17.19. 消失的两个数字

给定一个数组，包含从 1 到 N 所有的整数，但其中缺了两个数字。你能在 O(N) 时间内只用 O(1) 的空间找到它们吗？

以任意顺序返回这两个数字均可。
本题是上面出现的两道题的一个综合
在这里插入图片描述

class Solution {
    public int[] missingTwo(int[] nums) {
        int tmp = 0;
        for(int x: nums) tmp ^= x;
        for(int i = 1;i <= nums.length + 2;i++) {
            tmp ^= i;
        }
        int ret = (tmp & (-tmp));
        int[] arr = new int[2];
        for(int i = 0;i < nums.length;i++) {
            if((ret & nums[i]) == ret) {
                arr[0] ^= nums[i];
            } else {
                arr[1] ^= nums[i];
            }
        }
        for(int i = 1;i <= nums.length + 2;i++) {
            if((ret & i) == ret) {
                arr[0] ^= i;
            } else {
                arr[1] ^= i;
            }
        }
        return arr;
    }
}