2023.7.14

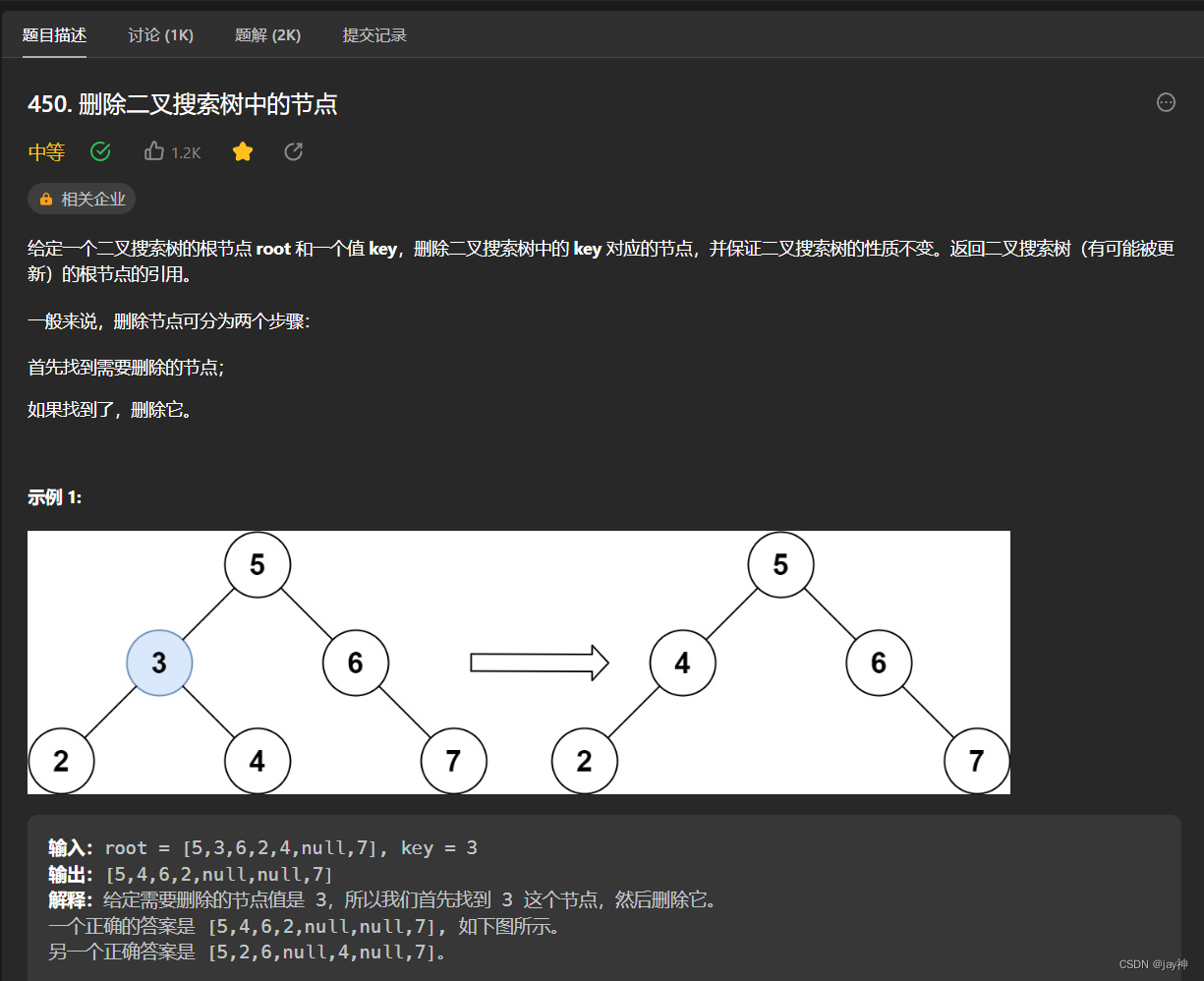
       搜索二叉树相关的题一般都能用递归解决。

        本体大致思路是：使用递归的方式，在树中查找目标节点，并根据节点的情况进行删除操作。如果目标节点是叶子节点，直接删除它；如果目标节点只有一个子树，将子树替代目标节点；如果目标节点有两个子树，找到右子树中的最小节点，将其值赋给目标节点，并递归删除右子树中的最小节点。通过递归的处理，最终返回修改后的二叉搜索树。 

        细节看代码：

递归法：

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(root == nullptr) return root;
        if(root->val > key) root->left = deleteNode(root->left,key);
        if(root->val < key) root->right = deleteNode(root->right,key);
        if(root->val == key)
        {
            //需要删除的节点 既无左子树也无右子树 通过返回nullptr来表示删除该节点
            if(!root->left && !root->right)
            {
                return nullptr;
            }
            //需要删除的节点没有左子树/右子树  将子树返回，作为目标节点的替代节点
            else if(!root->left) 
            {
                return root->right;
            }
            else if(!root->right) 
            {
                return root->left;
            }
            // 既有左子树 又有右子树
            else
            {   
                //找到右子树的最左边节点 将节点值赋给目标节点 然后递归调用 deleteNode 函数，删除右子树中的最小节点
                TreeNode* cur = root->right;
                while(cur->left != nullptr) cur = cur->left;
                root->val = cur->val;
                root->right = deleteNode(root->right,root->val);
            }
        }
        return root;
    }
};

        日后二刷。

---

普通二叉树删除法：

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(root == nullptr) return root;
        if(root->val == key)
        {
            if(root->right == nullptr) return root->left;
            TreeNode* cur = root->right;
            while(cur->left)
            {
                cur = cur->left;
            }
            swap(root->val,cur->val);
        }
        root->left = deleteNode(root->left,key);
        root->right = deleteNode(root->right,key);
        return root;
    }
};