
主程序:
%
ex=importdata('data3.txt');
tx = regexp(ex{1}, '\s+', 'split');%按照空格分隔字符串,成为单个cell
yx=str2double(tx);
plot(yx);
ww=yx(2500:9000)-2055;
Fyz_fft(ww,1000);
傅里叶封装函数:
function Fyz_fft(y,Fs)
% Demon:
% Fs = 128; % 采样频率
% T = 1/Fs; % 采样时间
% L = 256; % 信号长度
% t = (0:L-1)*T; % 时间
% y = 5 + 7*cos(2*pi*15*t - 30*pi/180) + 3*cos(2*pi*40*t - 90*pi/180); %cos为底原始信号
dataLen = length(y); %获取声音长度
t=(0:dataLen-1)/Fs;
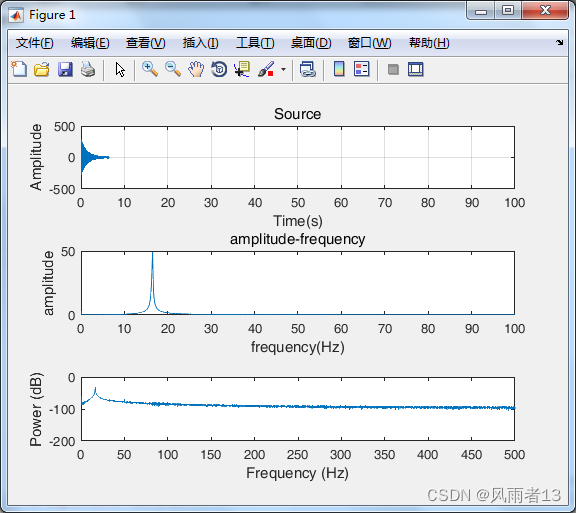
subplot(3,1,1);
plot(t, y), title('Source'),grid; %波形图
xlim([0,100]);
xlabel('Time(s)');
ylabel('Amplitude');
% Y = fft(X) 使用快速傅里叶变换算法返回向量X的离散型傅里叶变换
% Y = fft(X,n) 返回n点的离散傅里叶变换,如果向量X的长度小于n,函数要将向量X补零到长度n;如果向量X的长度大于n, 则函数阶段X使之长度为n。若X是矩阵,按相同方法对X进行处理。
N = 2^nextpow2(dataLen); %采样点数,采样点数越大,分辨的频率越精确,N>=L,超出的部分信号补为0
Y = fft(y,N)/N*2; %除以N乘以2才是真实幅值,N越大,幅值精度越高
f = Fs/N*(0:1:N-1); %频率
A = abs(Y); %幅值
subplot(3,1,2);plot(f(1:N/2),A(1:N/2)); %函数fft返回值的数据结构具有对称性,因此我们只取前一半
xlim([0,100]);
title('amplitude-frequency');
xlabel('frequency(Hz)');
ylabel('amplitude');
% P = angle(Y); %相值
% subplot(3,1,3);plot(f(1:N/2),P(1:N/2));
% title('phase-frequency');
% xlabel('frequency(Hz)');
% ylabel('phase');
% 请参照 http://www.mathworks.com/support/tech-notes/1700/1702.html
xdft = Y(1:N/2+1);
psdx = (1/(Fs*N)) * abs(xdft).^2;
psdx(2:end-1) = 2*psdx(2:end-1);
freq = f(1:N/2+1);
subplot(3,1,3);
plot(freq,10*log10(psdx));%注意这是dB显示,不然就成了频率谱了
% xlim([0,1000]);
xlabel('Frequency (Hz)');
ylabel('Power (dB)');
end



![[附源码]JAVA毕业设计线上导医系统(系统+LW)](https://img-blog.csdnimg.cn/2a10e38a875643f6a3e4df8047dad027.png)






![[附源码]JAVA毕业设计无人驾驶汽车管理系统(系统+LW)](https://img-blog.csdnimg.cn/23e25721c8c444b8992cdebd1ef97301.png)
![[附源码]JAVA毕业设计西藏民族大学论文管理系统(系统+LW)](https://img-blog.csdnimg.cn/acdcaa5435ab44de8f85230231af9c86.png)