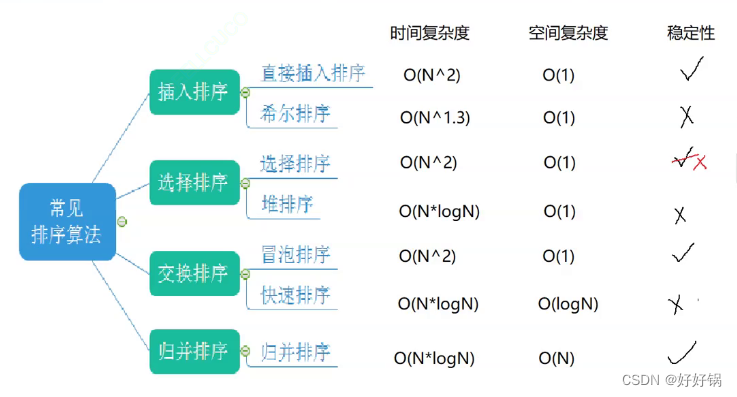
快速排序的整体介绍

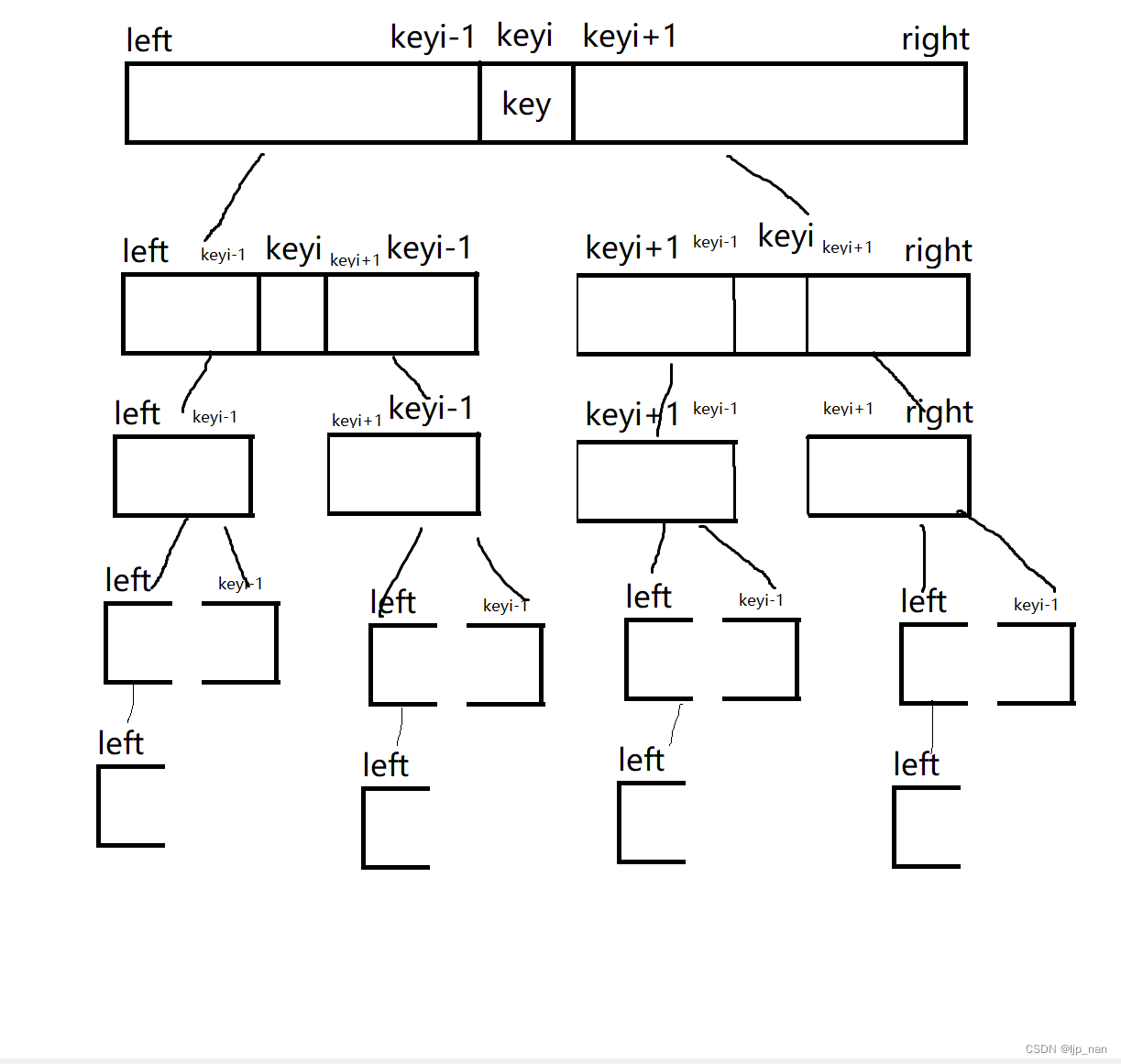
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。它可以先写出一趟快排，再使用递归的算法进行下一趟的排序，把left和right区间划分为了三个部分
[left keyi-1] keyi [keyi+1,right]。
每次排序，keyi的值改变就会变化，把区间分割的越来越小，每个区间再使用一趟快排，整个区间就会有序。递归条件为区间里的数字个数剩余一个和没有区间。[left keyi-1] 和 [keyi+1,right]递归排序，把l如下图所示：

hoare

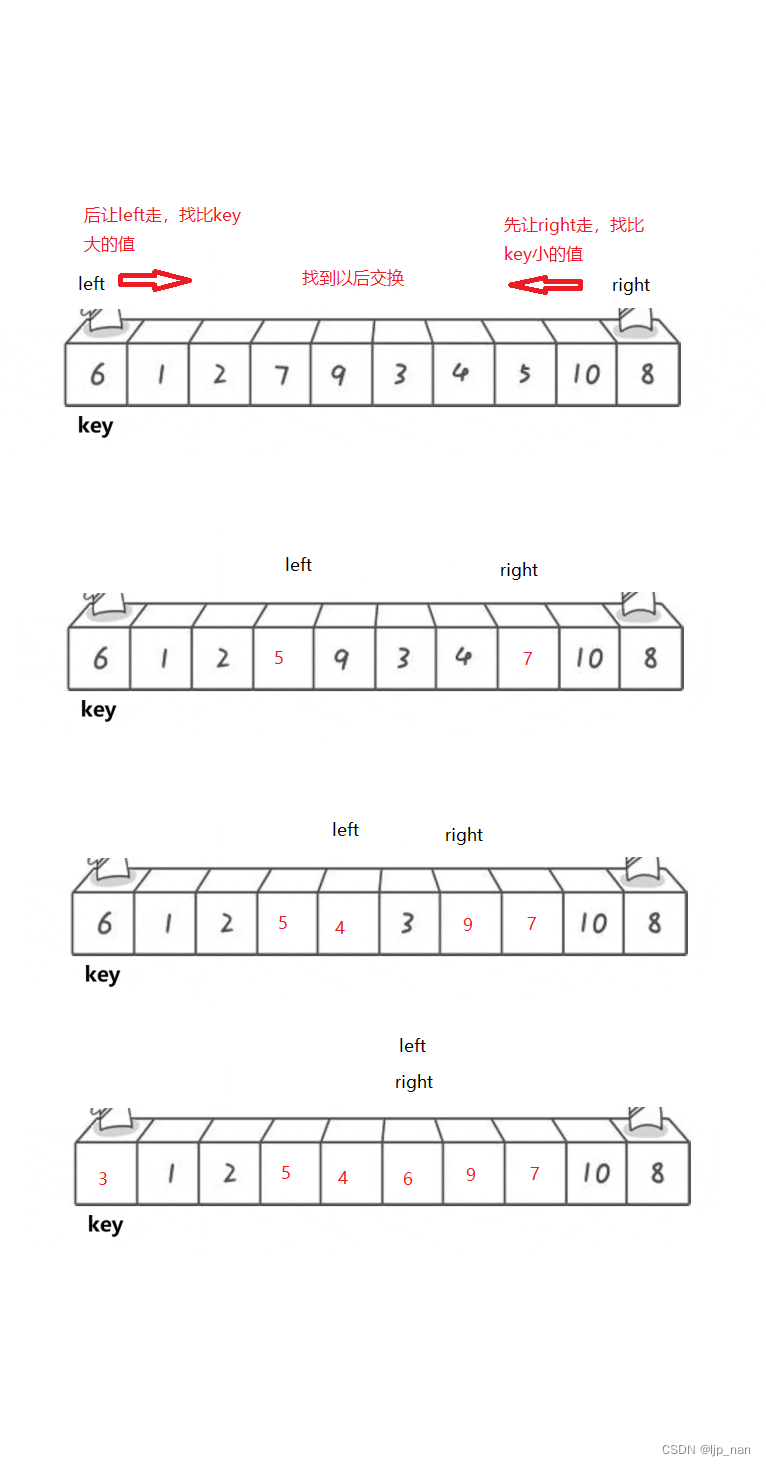
思路

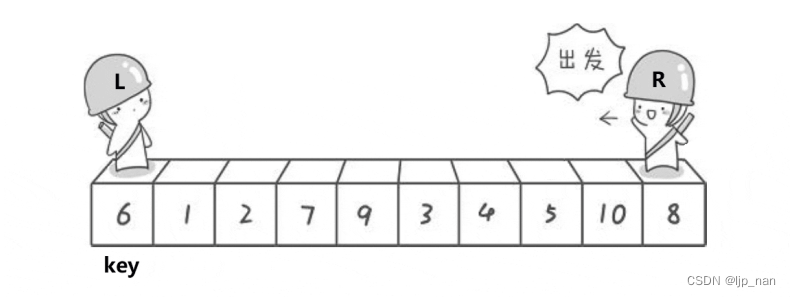
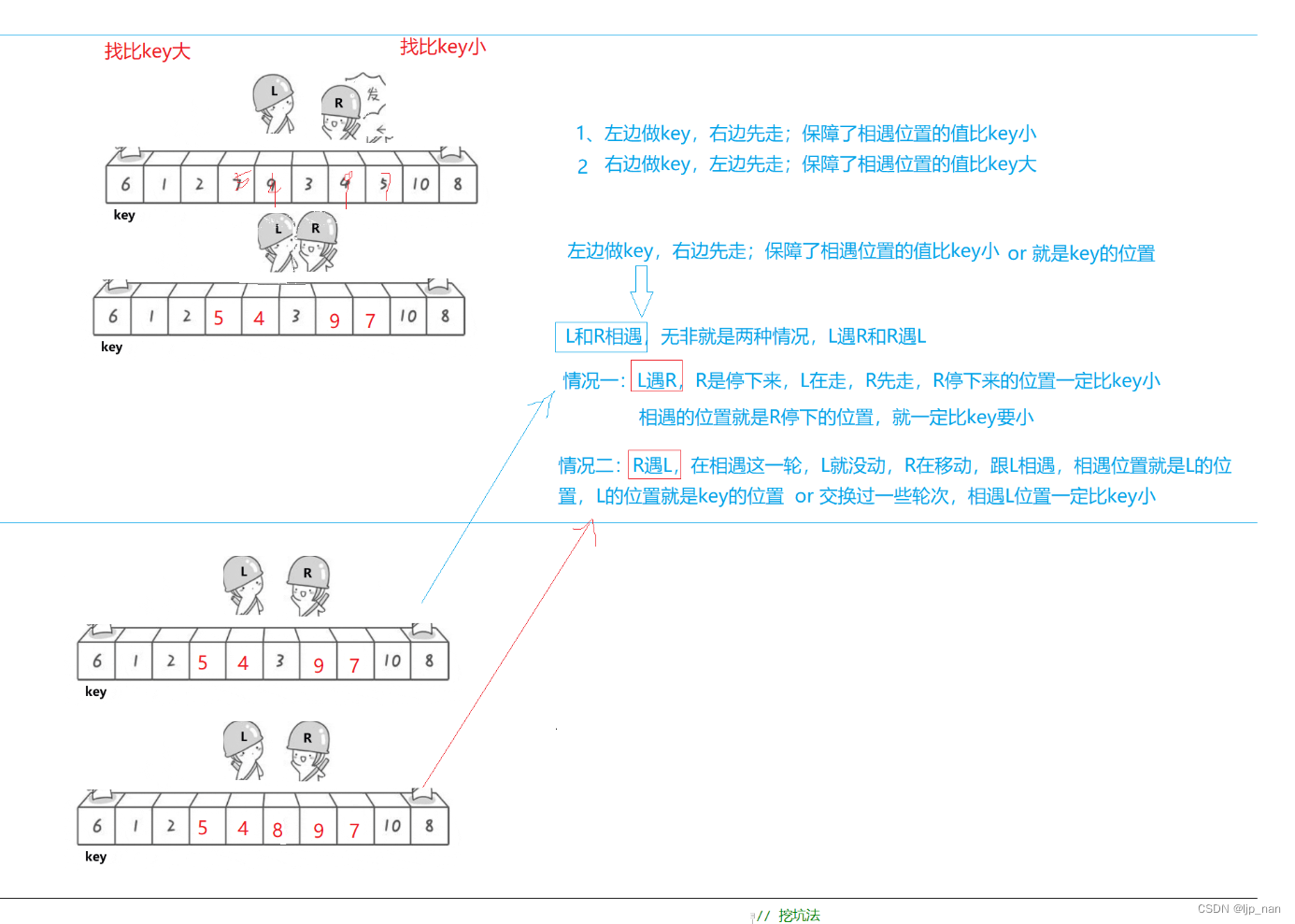
思路：定义两个指针，让right先走，找到比key值小的和left的值交换，然后left走找到大的和key的值交换。直至key左边的值是小于key的，在key右边的值是大于key的。这里需要讨论为什么先让R走。而不是先让left走。我们先来把过程图画一画：

hoare版本的说明：

代码实现

//hoare版本
int PastSort1(int* a, int left, int right)
{
	//选取key为最左边的值。
	int keyi = left;
	//left和right相遇后就不会进入循环
	while (left < right)
	{
		while (left<right && a[right] >= a[keyi]) //我们还得考虑右边的值都是大于key和left或者right所指向的值相等的情况。
		{
			right--;
		}
		while (left<right && a[left] <= a[keyi])
		{
			left++;
		}
		//交换最大值和最小值
		Swap(&a[left], &a[right]);
	}
	//左右指针相遇后一定是比key小的值。
	//把key和left的值交换
	Swap(&a[left], &a[keyi]);
	return left;
	
}


void QuickSort(int* a, int left, int right)
{
	if (left > right)
	{
		return;
	}
	int keyi = PastSort1(a, left, right);
	//把left和right区间分为了左右两个区间
	//[left keyi - 1] keyi[keyi + 1, right]
	//然后调用递归算法让他们排序。
	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi+1, right);
}

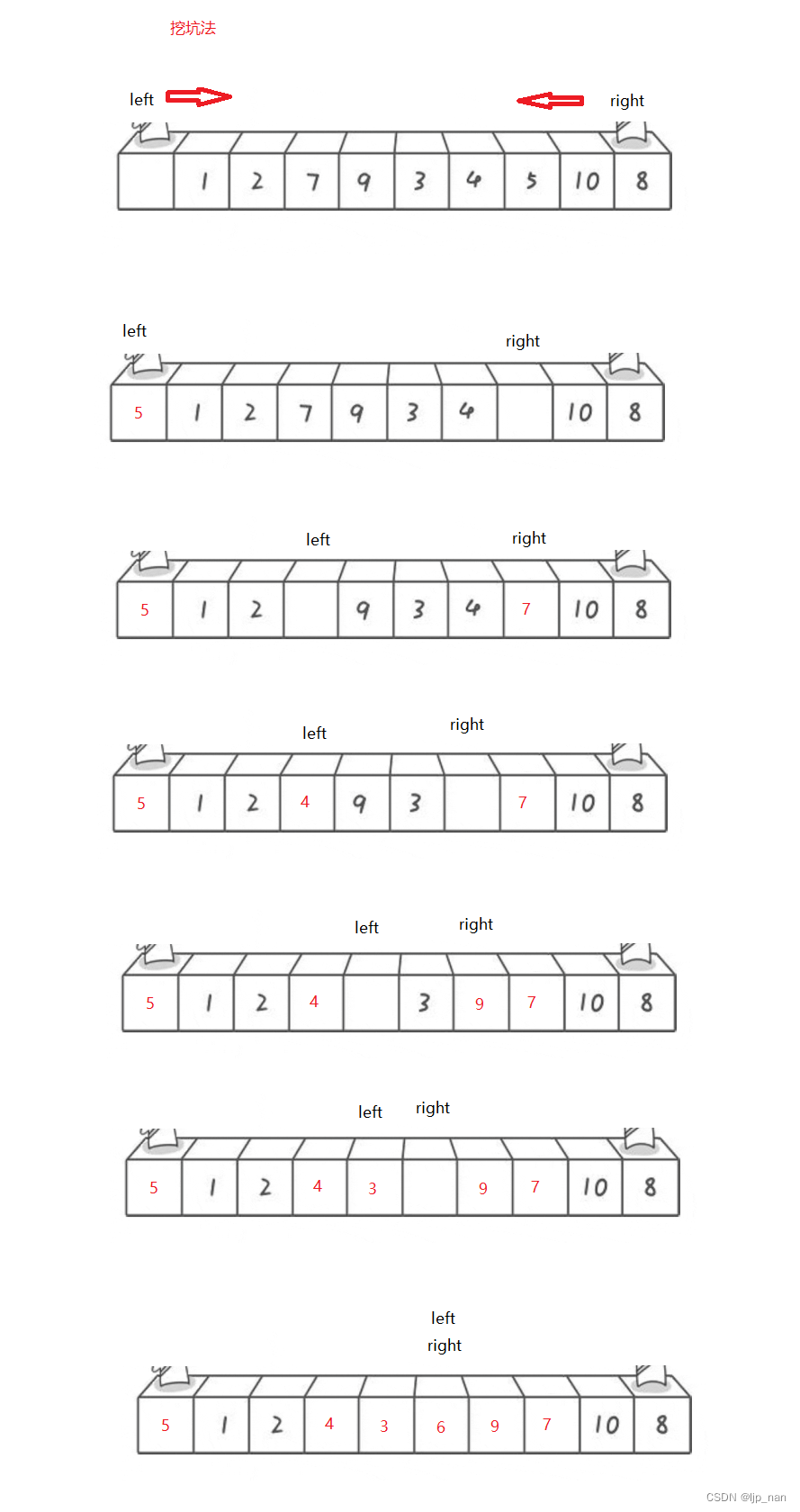
挖坑法

思路

先找出key的位置为keyi 然后找到比key小的值交换，keyi的位置产生一个坑然后找到最大的

代码实现

//挖坑法
int PastSort2(int* a, int left, int right)
{
	//选取key为最左边的值。
	int key = a[left];
	int hole = left;
	while (left < right)
	{
		while (left < right && a[right] >= key)
		{
			right--;
		}
		//从右边找到比key小的填坑
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] <= key)
		{
			left++;
		}
		//从左边找到比key大的填坑
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;
	return hole;
}

前后指针法

思路

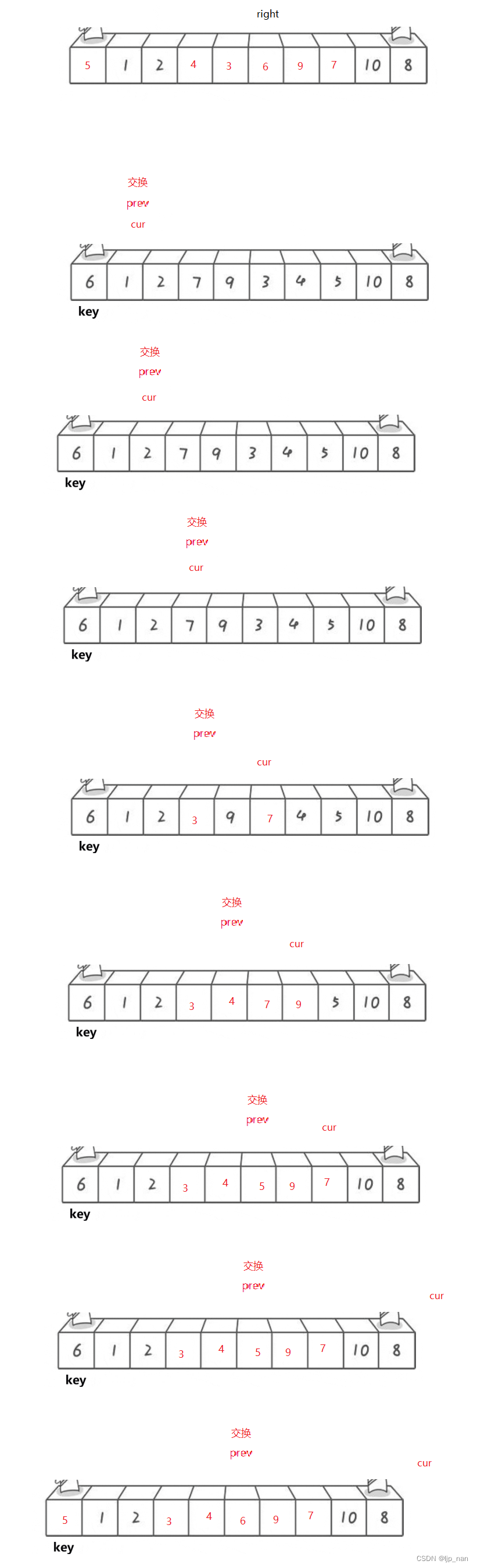
代码实现

//前后指针法
int PastSort3(int* a, int left, int right)
{
	int keyi = left;
	int prev = left;
	int cur = left + 1;

	while (cur <= right)
	{
		if (a[cur] < a[keyi])
		{
			Swap(&a[++prev], &a[cur]);
		}
		cur++;
	}
	Swap(&a[prev], &a[keyi]);
	return prev;
}