理论基础
种类
满二叉树、完全二叉树、二叉搜索树
满二叉树
如果一颗二叉树只有度为0的节点和度为2的节点,并且度为0的节点都在同一层
完全二叉树
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。
二叉搜索树
二叉搜索树是一个有序树
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树

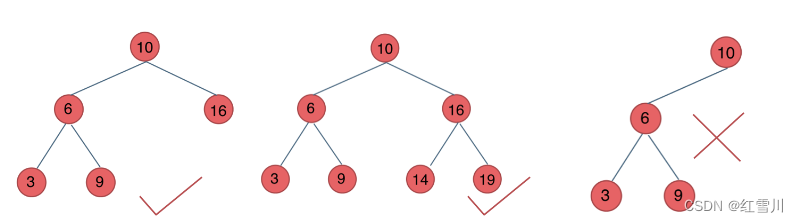
平衡二叉搜索树
又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
存储方式
链式存储、线式存储
遍历方式
- 深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历
- 层次遍历(迭代法)
定义方式
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {} // 构造函数
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};递归遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
//前序
class Solution {
public:
void traver(TreeNode* cur, vector<int>& vec){
if (cur == nullptr)
return;
vec.push_back(cur->val);
traver(cur->left, vec);
traver(cur->right, vec);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
traver(root, res);
return res;
}
};
//中序
class Solution {
public:
void traver(TreeNode* root, vector<int>& cur){
if (root == nullptr)
return;
traver(root->left, cur);
traver(root->right, cur);
cur.push_back(root->val);
}
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
traver(root, res);
return res;
}
};
//后序
class Solution {
public:
void traver(TreeNode* cur, vector<int>& res){
if (cur == nullptr)
return;
traver(cur->left, res);
res.push_back(cur->val);
traver(cur->right, res);
}
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
traver(root, res);
return res;
}
};