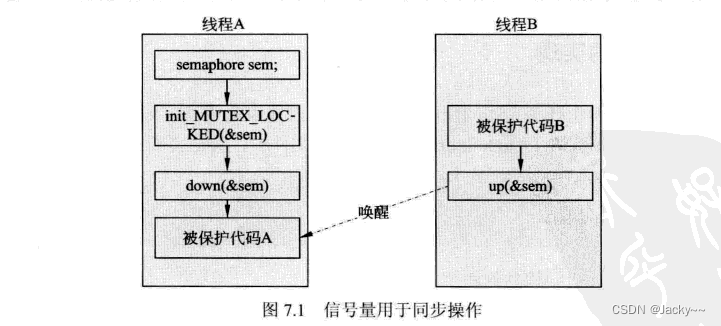
代码展示：

class Solution {
    public int maxValue(int[][] grid) {
        int m=grid.length;
        int n=grid[0].length;

        //创建dp数组
        int[][]dp=new int[m+1][n+1];
        //填充数组
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
            }
        }

        return dp[m][n];
    }
}

        进行动态规划的五个步骤：

        1.状态表示

                dp[i][j]表示从起点到[i][j]这个位置上能获得礼物的最大价值

        2.状态转移方程

                我们分析距离[i][j]最近的位置，根据题意我们到达[i][j]位置只能从[i-1][j]向下移动或者从

[i][j-1]向右移动，所以我们如何判断哪种方式下我们可以获得更大的价值呢，那就选择在最大价值的位置进行移动，而[i-1][j]和[i][j-1]的最大价值为dp[i-1][j]和dp[i][j-1],我们比较两者的值，从更大的价值的位置进行移动，移动后再加上[i][j]位置上自己的价值，便得到了dp[i][j]的值

        所以我们得到状态转移方程 dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1],由于在创建dp数组时增加了辅助结点，相比于grid数组多了一行一列，所以两个数组之间的映射也发生了改变dp[i][j]对应grid[i-1][j-1]

        3.初始化，通过具体示例分析，应该将第一行和第一列初始化为0才满足要求，而数组在创建时里面的数据就已经是0，所以没有写初始化的代码

        4.从上到下，从左到右依次填充数组

        5返回dp[m][n]的值