题目

一个长度为L(L>=1)的升序序列S，处在第[L/2]个位置的数称为S的中位数。例如，若序列S1={11,13,15,17,19},则S1的中位数是15，两个序列的中位数是含它们所有元素的升序序列的中位数，例如，若S2={2,4,6,8,20}，则S1和S2的中位数是11。现在有两个等长升序序列A和B，试设计一个在时间和空间两方面都尽可能高效的算法，找出两个序列A和B的中位数。要求：

给出算法的基本设计思想。
根据设计思想，用C/C++实现算法。
说明所设计的算法的时间复杂度和空间复杂度。

基本设计思想

根据题目要求，主要要求将两个升序序列合并为整体升序序列并返回整体序列中的中位数。
因此，我们可以考虑现根据给出两个升序序列的元素个数，计算出中位数再最终整体有序序列中的存在位置X。
然后，利用双指针算法，设置指针i,j分别指向序列A和序列B，升序合并两个序列过程中与计算出的中位数下标比较，若相等，则返回第X个元素，即为题目所要求的中位数。

代码实现

int LinearList::Question_11()
{
    Array arr1,arr2;
    arr1.length = 5;
    cout<<"insert 5 nums to arr1:"<<endl;
    for(int i = 0;i < arr1.length;i ++)
    {
        cin >> arr1.data[i];
    }

    arr2.length = 5;
    cout<<"insert 5 nums to arr2:"<<endl;
    for(int i = 0;i < arr2.length;i ++)
    {
        cin >> arr2.data[i];
    }

    arr.length = arr1.length + arr2.length;

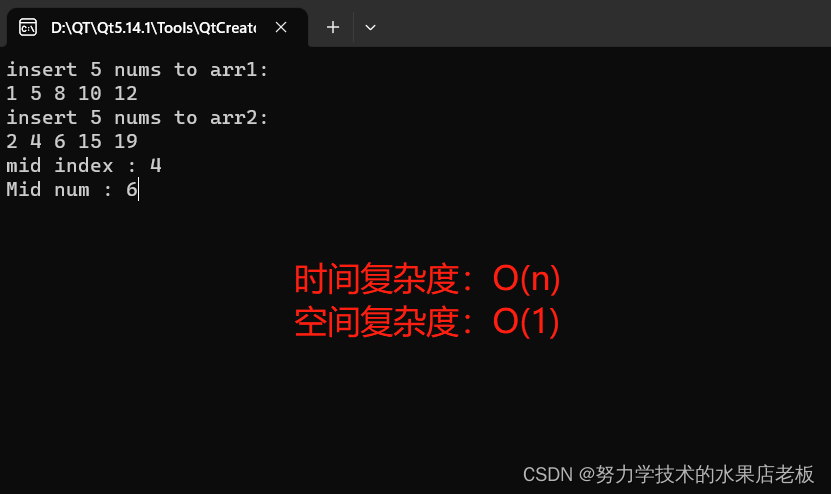
    int mid = arr.length/2 - 1;   //计算最终升序序列中位数坐在位置下标
    cout << "mid index : "<<mid<<endl;

    int i = 0,j = 0;    //设置哨兵i,j分别指向数组arr1和数组arr2
    int k = 0;          //设置变量k记录最终升序序列元素下标

    while(i < arr1.length && j < arr2.length)
    {
        if(arr1.data[i] <= arr2.data[j])
        {
            if(k == mid)    //判断是否为中位数下标
            {
                cout<< "Mid num : "<<arr1.data[i];
                return arr1.data[i];
            }
            k++;
            i++;
        }
        else
        {
            if(k == mid)    //判断是否为中位数下标
            {
                cout<< "Mid num : "<<arr2.data[j];
                return arr2.data[j];
            }
            k++;
            j++;
        }
    }

    while(i < arr1.length)
    {
        if(k == mid)    //判断是否为中位数下标
        {
            cout<< "Mid num : "<<arr1.data[i];
            return arr1.data[i];
        }
        k++;
        i++;
    }

    while(j < arr2.length)
    {
        if(k == mid)    //判断是否为中位数下标
        {
            cout<< "Mid num : "<<arr2.data[j];
            return arr2.data[j];
        }
        k++;
        j++;
    }
}