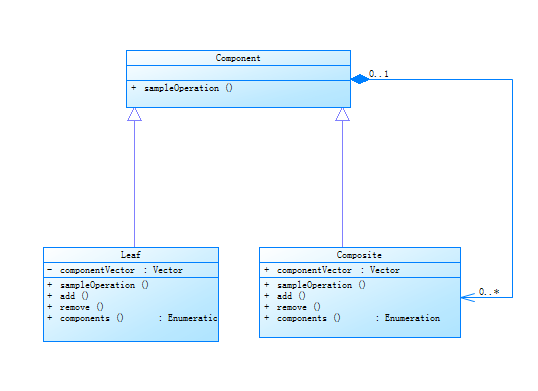
管理系统模型(仓库管理系统)—顺序表
操作对象之间的关系:线性关系 数据结构:线性数据结构、线性表 (例如:学生成绩管理系统、人事管理系统、仓库管理系统、通讯录等。)
操作对象:若干行数据记录
操作算法:查询、插入、修改、删除等
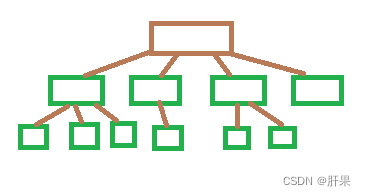
人机对弈模型(三子棋)—树
之所以能对弈:策略已经输入计算机,可以根据当前棋盘格局来预测棋局发展的趋势,甚至最后结局。
计算机的操作对象:各种棋局状态,即描述棋盘的格局信息
计算机的算法:走棋,即选择一种策略使棋局状态发生变化(由一个格局派生出另一个格局)
操作对象之间的关系:非线性关系、树
数据与数据成一对多的关系,是一种典型的非线性关系结构:树形结构。
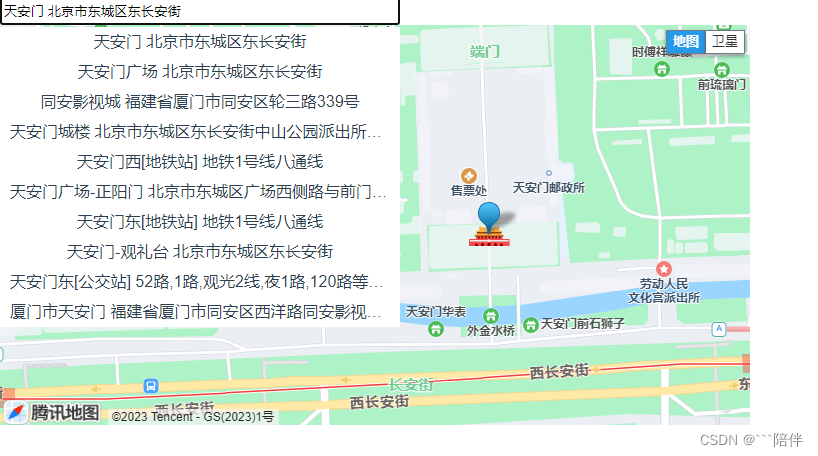
地理信息处理模型(高德地图)—图
地图导航最短路径
网状结构
问题:找到图中两点之间的最短路径或最经济路径
操作对象:各地点及路的信息。
计算机算法:设置信号灯,求出各个可同时通行的路的集合。
对象之间的关系:非线性关系,网状结构。
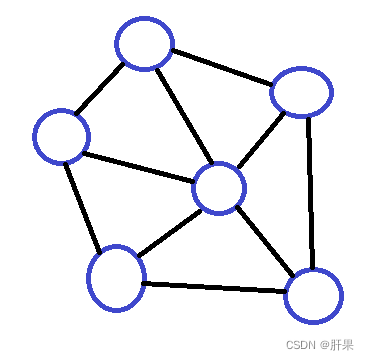
综上所述
这些问题的共性是都无法用数学的公式或方程来描述,是一些“非数值计算”的程序设计问题。
描述非数值计算问题的数学模型不是数学方程,而是诸如表、树和图之类的具有逻辑关系的数据。
数据结构是一门研究非数值计算的程序设计中计算机的操作对象以及它们之间的关系和操作的学科。
基本概念和术语
数据、数据元素、数据项和数据对象
数据是能输入计算机且能被计算机处理的各种符号的集合
数据元素是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理。也简称为元素,或称为记录、结点或顶点。
数据项构成数据元素的不可分割的最小单位。
数据、数据元素、数据项三者之间的关系:
数据>数据元素>数据项
例:参赛表>运动员记录>参赛编号、姓名……
数据对象是性质相同的数据元素的集合,是数据的一个子集。
例如:整数数据对象是集合N={0,±1,±2,…}
数据元素与数据对象
数据元素是组成数据的基本单位,与数据的关系:是集合的个体
数据对象是性质相同的数据元素的集合,与数据的关系是:集合的子集
数据结构
1、数据元素不是孤立存在的,它们之间存在着某种关系,数据元素相互之间的关系称为结构(Structure)
2、是指相互之间存在一种或多种特定关系的数据元素集合
3、或者说,数据结构是带结构的数据元素的集合
数据结构包括以下三个方面的内容:
1、数据元素之间的逻辑关系,也称为逻辑结构。
2、数据元素及其关系在计算机内存中的表示(又称为映像),称为数据的物理结构或数据的存储结构。
3、数据的运算和实现,即对数据元素可以施加的操作以及这些操作在相应的存储结构上的实现。
数据结构的两个层次
逻辑结构
1、描述数据元素之间的逻辑关系
2、与数据的存储无关,独立于计算机
3、是从具体问题抽象出来的数学模型
物理结构(存储结构)
1、数据元素及其关系在计算机存储器中的结构(存储方式)
2、是数据结构在计算机中的表示
逻辑结构与存储结构的关系
1、存储结构是逻辑关系的映象与元素本身的映象。
2、逻辑结构是数据结构的抽象,存储结构是数据结构的实现。
3、两者综合起来建立了数据元素之间的结构关系。
逻辑结构的种类
划分方法一
(1)线性结构
有且仅有一个开始和一个终端结点,并且所有结点都最多只有一个直接前趋和一个直接后继。
例如:线性表、栈、队列、串
(2)非线性结构
一个结点可能有多个直接前趋和直接后继
例如:树、图
一些在浏览技术博客过程中经常出现却因为没有学习数据结构而不了解所产生的问题,通过问ChatAI得出的解答:
问:链表在数据结构逻辑结构的划分中属于线性结构还是非线性结构?链表和栈,队列,串有关系吗?
答:
链表在数据结构中属于线性结构。
线性结构是指数据元素之间存在一对一的前后关系,链表就是一种典型的线性结构。在链表中,每个元素都包含一个指向下一个元素的指针,通过这种方式将所有元素按顺序连接起来。
链表与栈、队列、串都有关系,它们都是常见的数据结构,可以通过链表来实现。
- 栈(Stack)是一种后进先出(Last-In-First-Out,LIFO)的数据结构,可以通过链表来实现链式栈。
- 队列(Queue)是一种先进先出(First-In-First-Out,FIFO)的数据结构,可以通过链表来实现链式队列。
- 串(String)是由零个或多个字符组成的有限序列,可以通过链表来实现链式串。
通过使用链表来实现栈、队列、串等数据结构,可以灵活地进行插入、删除等操作,并且不需要事先知道数据元素的个数。
问:堆属于非线性结构中的一种特殊的树吗?
答:
是的,堆是非线性结构中的一种特殊的树。
在数据结构中,线性结构中的元素之间存在一对一的关系,例如链表、数组等。而非线性结构中的元素之间存在一对多的关系,例如树、图等。
堆是一种特殊的树型数据结构,它可以被视为一种完全二叉树(或者是近似完全二叉树)。在堆中,树中的每个节点都有一个值,而且具有以下两个特性:
- 最大堆(Max Heap):对于堆中的任意节点,其值都大于或等于其子节点的值。
- 最小堆(Min Heap):对于堆中的任意节点,其值都小于或等于其子节点的值。
堆常被用于实现优先队列等特殊的数据结构,其中元素的优先级由其在堆中的值决定。由于堆具有特殊的性质,可以高效地进行堆化、插入和删除等操作,常用于解决许多算法和数据处理问题。
划分方法二—四类基本逻辑结构
1、集合结构:结构中的数据元素之间除了同属于一个集合的关系外,无任何其他关系。
2、线性结构:结构中的数据元素之间存在着一对一的线性关系。
3、树形结构:结构中的数据元素之间存在着一对多的层次关系。
4、图状结构或网状结构:结构中的数据元素之间存在着多对多的任意关系。
存储结构的种类
四种基本的存储结构:
1、顺序存储结构
2、链式存储结构
3、索引存储结构
4、散列存储结构
顺序存储结构
1、用一组连续的存储单元依次存储数据元素,数据元素之间的逻辑关系由元素的存储位置来表示。
2、C语言中用数组来实现顺序存储结构。
链接存储结构:
1、用一组任意的存储单元存储数据元素,数据元素之间的逻辑关系用指针来表示。
2、C语言中用指针来实现链式存储结构。
索引存储结构:
1、在存储结点信息的同时,还建立附加的索引表。
例:通信录
2、索引表中的每一项称为一个索引项
3、索引项的一般形式是:(关键字,地址)
4、关键字是能唯一识别一个结点的那些数据项。
5、若每个结点在索引表中都有一个索引项,则该索引表称之为稠密索引。若一组结点在索引表中只对应一个索引项,则该索引表称之为稀疏索引。
散列存储结构
根据结点的关键字直接计算出该结点的存储地址。
散列存储结构,也称为哈希表,是一种常见的数据结构,用于存储和检索数据。它通过把数据映射到数组的特定位置来实现快速访问。
举个例子,假设我们要实现一个电话号码簿,其中存储了人名与对应的电话号码。我们可以使用散列存储结构来快速查找电话号码。
首先,我们创建一个具有固定大小的数组,大小根据预期存储的记录数确定。假设我们选择一个大小为10的数组。
接下来,我们定义一个散列函数,该函数将人名作为输入,并将其转换为整数。
例如,我们可以使用简单的散列函数,将每个人名的字符转换为ASCII码,并求和得到一个整数值。例如,“Alice"对应的ASCII码之和为65+108+105+99+101=478。
然后,我们使用散列函数计算每个人名对应的散列值,并将其作为索引值,将电话号码存储在数组中。
假设我们要存储电话号码簿中的三个记录:
Alice: 1234567890
Bob: 9876543210
Carol: 4567890123
使用散列函数,将它们映射到数组中的位置:
Alice -> 散列值: 478 -> 存储在数组索引为8的位置
Bob -> 散列值: 308 -> 存储在数组索引为8的位置(发生碰撞)
Carol -> 散列值: 649 -> 存储在数组索引为9的位置
在查询电话号码时,我们只需使用相同的散列函数,将人名转换为散列值,并在数组中查找该位置的数据。
例如,要找到Bob的电话号码,我们将散列函数应用于"Bob”,得到散列值308,然后在索引为8的数组位置找到电话号码9876543210。
这就是散列存储结构的基本原理。它提供了快速的插入和查找操作,使得访问大量数据变得高效。
当然,实际的散列存储结构可能会使用更复杂的散列函数和解决碰撞的方法,但以上示例展示了其基本概念和用法。
数据类型和抽象数据类型
1、在使用高级程序设计语言编写程序时,必须对程序中出现的每个变量、常量或表达式,明确说明它们所属的数据类型。
例如,C语言中:
提供int,char,float,double等基本数据类型
数组、结构、共用体、枚举等构造数据类型
指针、空(void)类型
用户也可以typedef自己定义数据类型
2、一些最基本数据结构可以用数据类型来实现,如数组、字符串等。
3、而另一些常用的数据结构,如栈、队列、树、图等,不能直接用数据类型来表示。
4、高级语言中的数据类型明显地或隐含地规定了在程序执行期间变量和表达的所有可能的取值范围,以及在这些数值范围上所允许进行的操作。
例如:C语言中定义变量i为int类型,就表示i是[-min,max]范围的整数,在这个整数集上可以进行+、-、*、\、%等操作
5、数据类型的作用
①、约束变量或常量的取值范围
②、约束变量或常量的操作
数据类型
定义:数据类型是一组性质相同的值的集合以及定义于这个值集合上的一组操作的总称。
数据类型=值的集合+值集合上的一组操作
抽象数据类型
是指一个数学模型以及定义在此数学模型上的一组操作。
1、由用户定义,从问题抽象出数据模型(逻辑结构)
2、还包括定义在数据模型上的一组抽象运算(相关操作)
3、不考虑计算机内的具体存储结构与运算的具体实现算法
抽象数据类型的形式定义
抽象数据类型可用(D,S,P)三元组表示。
其中:
D是数据对象;
S是D上的关系集;
P是对D的基本操作集。
一个抽象数据类型的定义格式如下:
ADT 抽象数据类型名{
数据对象:<数据对象的定义>
数据关系:<数据关系的定义>
基本操作:<基本操作的定义>
}抽象数据类型名
其中:
1、数据对象、数据关系的定义用伪代码描述
2、基本操作的定义格式为:
基本操作名(参数表)
初始条件:(初始条件描述)
操作结果:(操作结果描述)
基本操作定义格式说明:
参数表:赋值参数只为操作提供输入值。
引用参数以&打头,除可提供输入值外,还将返回操作结果。
初始条件:描述操作执行之前数据结构和参数应满足的条件,若不满足,则操作失败,并返回相应出错信息。若初始条件为空,则省略之。
操作结果:说明操作正常完成之后,数据结构的变化状况和应返回的结果。
抽象数据类型(ADT)定义举例:Circle的定义
ADT抽象数据类型名{
Data
数据对象的定义
数据元素之间逻辑关系的定义
Operation
操作1
初始条件
操作结果描述
操作2
……
操作n
……
}ADT抽象数据类型名
ADT Circle{
数据对象:D={r,x,y|r,x,y均为实数}
数据关系:R={<r,x,y>|r是半径,<x,y>是圆心坐标}
基本操作:
Circle(&C,r,x,y)
操作结果:构造一个圆。
double Area©
初始条件:圆已存在。
操作结果:计算面积。
double Circumference©
初始条件:圆已存在。
操作结果:计算周长。
……
}ADT Circle
抽象数据类型(ADT)定义举例:复数的定义
ADT Complex{
D={r1,r2|r1,r2都是实数}
S={<r1,r2>|r1是实部,r2是虚部}
assign(&C,v1,v2)
初始条件:空的复数C已存在
操作结果:构造复数C,r1,r2分别被赋以参数v1,v2的值。
destroy(&C)
初始条件:复数C已存在
操作结果:复数C被销毁
}ADT Complex
抽象数据类型中的基本操作:
Assign(&Z,v1,v2)
操作结果:构造复数Z,其实部和虚部,分别被赋以参数v1,v2值。
Destroy(&Z)
操作结果:复数Z被销毁。
GetReal(Z,&realPart)
初始条件:复数已存在。操作结果:用realPart返回复数Z的实部值。
GetImag(Z,&ImagPart)
初始条件:复数已存在。操作结果:用ImagPart返回复数Z的虚部值。
Add(z1,z2,&sum)
初始条件:z1,z2是复数。操作结果:sum返回两个复数z1,z2的和。
……
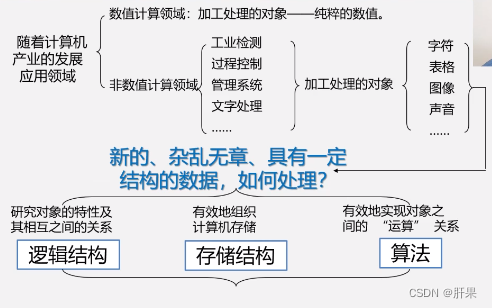
注:截图转自王卓数据结构教学视频
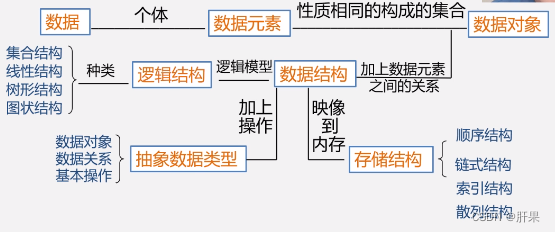
注:截图转自王卓数据结构教学视频
抽象数据类型的表示与实现
一个问题抽象为一个抽象数据类型后,仅是形式上的抽象定义,还没有达到问题解决的目的,要实现这个目标,就要把抽象的变成具体的,即抽象数据类型在计算机上实现,变成一个能用的具体的数据类型。
C语言实现抽象数据类型
1、用已有数据类型定义描述它的存储结构
2、用函数定义描述它的操作
抽象数据类型可以通过固有的数据类型(如整型、实型、字符型等)来表示和实现。
即利用处理器中已存在的数据类型来说明新的结构,用已经实现的操作来组合新的操作。
用C语言实现抽象数据类型的定义
例如:抽象数据类型“复数”的实现:
typedef struct{
float realpart; //实部
float imagpart; //虚部
}Complex //定义复数抽象类型
void assign(Complex* A,float real,float imag); //赋值
void add(Complex* A,float real,float imag); //A+B
void minus(Complex* A,float real,float imag); //A-B
void multiply(Complex* A,float real,float imag); //A*B
void divide(Complex* A,float real,float imag); //A/B
void assign(Complex* A,float real,float imag)
{
A->realpart=real; //实部赋值
A->imagpart=imag; //虚部赋值
//End of assign()
}
... ... ... ...