题目传送门

[USACO1.5] 八皇后 Checker Challenge

题目描述

一个如下的 $6\times 6$ 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

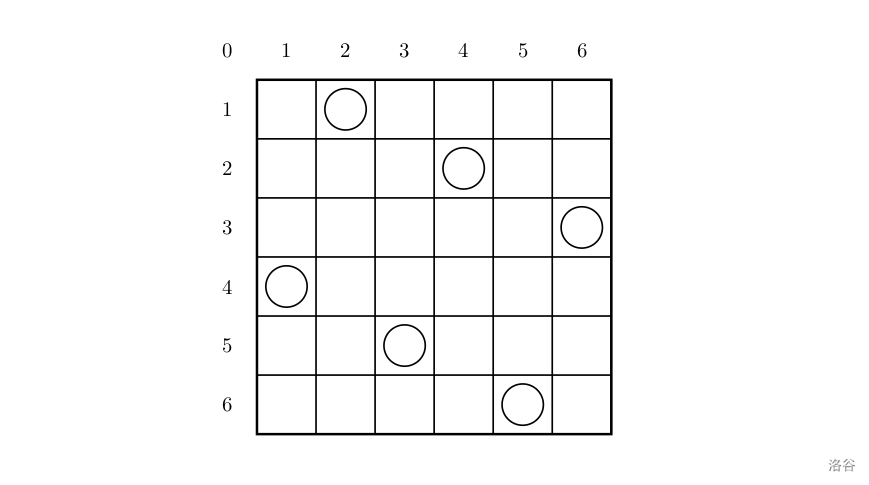
上面的布局可以用序列 $246135$ 来描述，第 $i$ 个数字表示在第 $i$ 行的相应位置有一个棋子，如下：

行号 $123456$

列号 $246135$

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 $3$ 个解。最后一行是解的总个数。

输入格式

一行一个正整数 $n$，表示棋盘是 $n\times n$ 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

样例 #1

样例输入 #1

6

样例输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

提示

【数据范围】
对于 $100\%$ 的数据，$6\le n\le 13$。

题目翻译来自NOCOW。

USACO Training Section 1.5

---

思考：

注意到题目给我们的输出方式，是以行为顺序输出相应棋子的列号的。
所以我们不难想到这道题需要以行号为搜索状态进行搜索。
每一行只能放一个棋子，所以我们在每一行中只要直接枚举当前行棋子的列号就可以了。
如何判断当前棋子是否能放呢？
注意棋子能放的条件：每行每列每条对角线只能有一颗棋子。
行号是我们搜索的状态，所以不用管，直接保证了每行只能有一颗棋子
我们只需要用三个数组分别表示当前列，两条对角线棋子的放置情况就可以了。
列好表示，直接用$L[i]$表示第i列是否有棋子就可以了。
那么对角线呢？
在这里我们就需要用到对角线的性质：

• 对于同一条左对角线上的点我们不难发现行和列的坐标和是一样的。
• 而右对角线响应的是行和列的坐标差是一样的。

利用这个性质我们分别用$Z[i]$和$Y[i]$去存储行列的和差情况即可。

---

#include<bits/stdc++.h>
using namespace std;

int Ans = 0;
int a[20];
int n;
int L[50],Z[50],Y[50];

void Work(){
	Ans++;
	if (Ans <= 3){
	    for (int i = 1; i < n; i++) printf("%d ",a[i]);
	    printf("%d\n",a[n]);
	}
}

void Dfs(int now){
	if (now == n+1) {Work();return;}
	for (int i = 1; i <= n; i++)
	  if (!L[i] && !Z[now-i+n] && !Y[now+i]){
	  	L[i] = 1; Z[now-i+n] = 1; Y[now+i] = 1;
	  	a[now] = i;
	  	Dfs(now+1);
	  	L[i] = 0; Z[now-i+n] = 0; Y[now+i] = 0;
	  }
}

int main(){
	scanf("%d",&n);
	Dfs(1);
	printf("%d",Ans);
}