专注 效率 记忆
预习 笔记 复习 做题

欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
　
文章字体风格：
红色文字表示：重难点★✔
蓝色文字表示：思路以及想法★✔
　
如果大家觉得有帮助的话，感谢大家帮忙
点赞！收藏！转发！

本博客带大家一起学习，我们不图快，只求稳扎稳打。
由于我高三是在家自学的，经验教训告诉我，学习一定要长期积累，并且复习，所以我推出此系列。
只求每天坚持40分钟，一周学5天，复习2天
也就是一周学10道题
60天后我们就可以学完81道题，相信60天后，我们一定可以有扎实的代码基础！我们每天就40分钟，和我一起坚持下去吧！
qq群：878080619

八、拓扑排序

1. 有向图的拓扑序列

原题链接

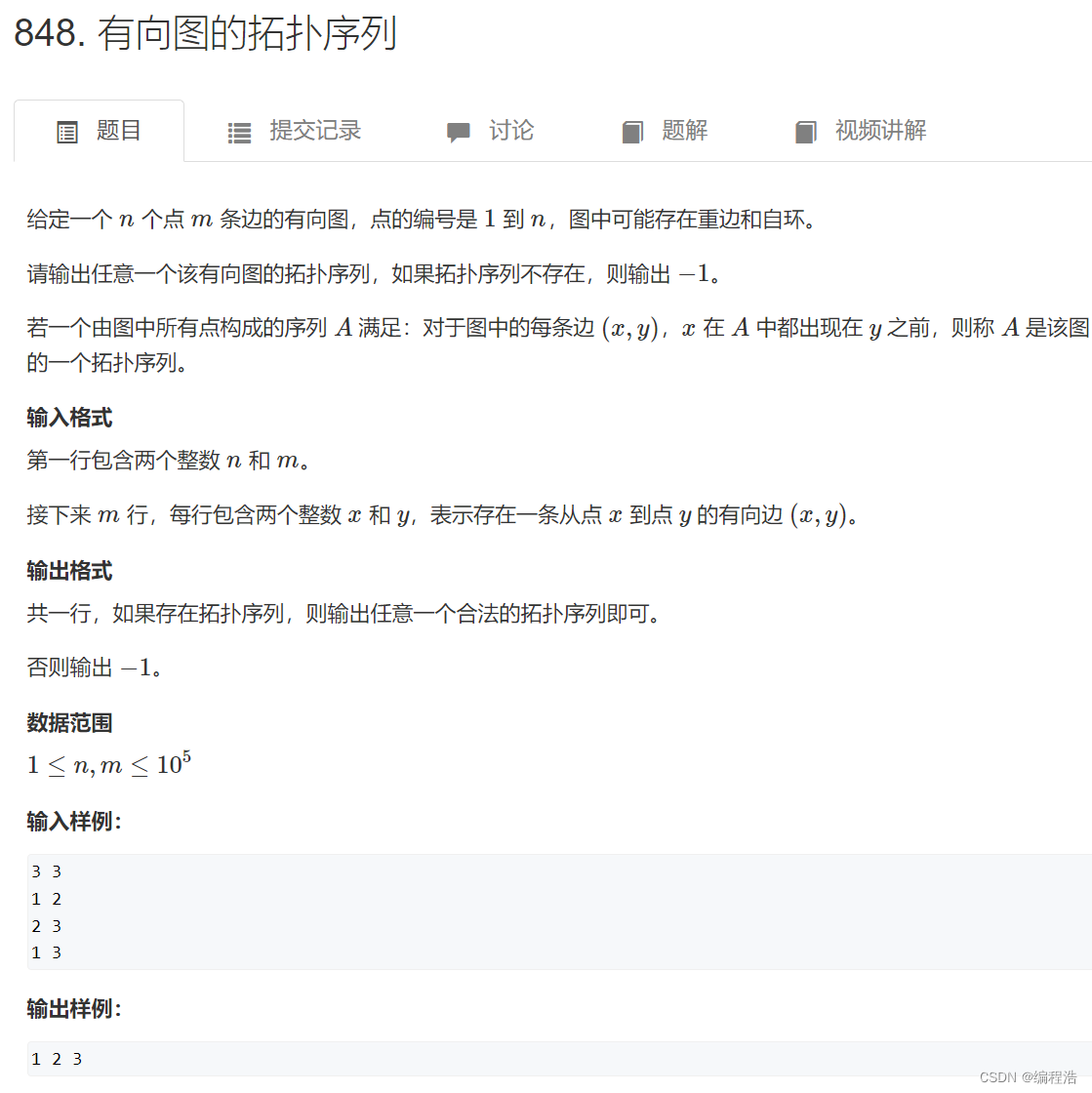
这就是一个模板
算法原理可以csdn搜一下

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int h[N], e[N], ne[N], idx;
int d[N];
int q[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool topsort()
{
    int hh = 0, tt = -1;

    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (-- d[j] == 0)
                q[ ++ tt] = j;
        }
    }

    return tt == n - 1;
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);

        d[b] ++ ;
    }

    if (!topsort()) puts("-1");
    else
    {
        for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);
        puts("");
    }

    return 0;
}

九、最小生成树、最短路

1. Prim算法求最小生成树

原题链接

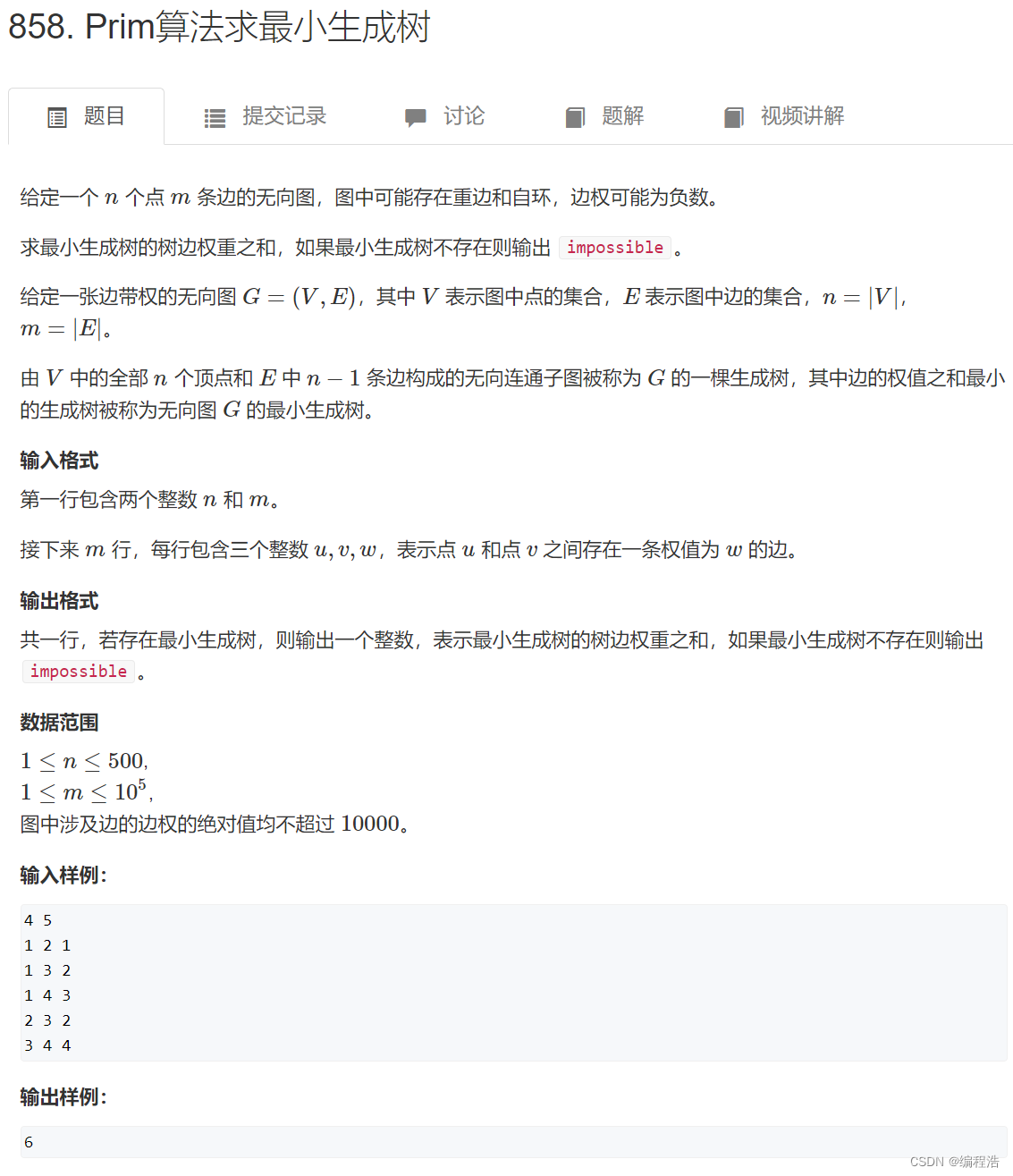
从1节点出发，每次走最短路径（距离集合的最短路径用d表示）选出最短路径再加到res上
（prim算法和dijkstra算法差不多，只是d的表示含义不同）

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 510, M = 100010, INF = 0x3f3f3f3f;

int n, m;
int g[N][N], dist[N];
bool st[N];

int prim()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                 t = j;
        if (dist[t] == INF) return INF;
        st[t] = true;
        res += dist[t];
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], g[t][j]);
    }
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(g, 0x3f, sizeof g);
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = g[b][a] = min(g[a][b], c);
    }

    int res = prim();
    if (res == INF) puts("impossible");
    else printf("%d\n", res);
    return 0;
}

2. Dijkstra求最短路 I

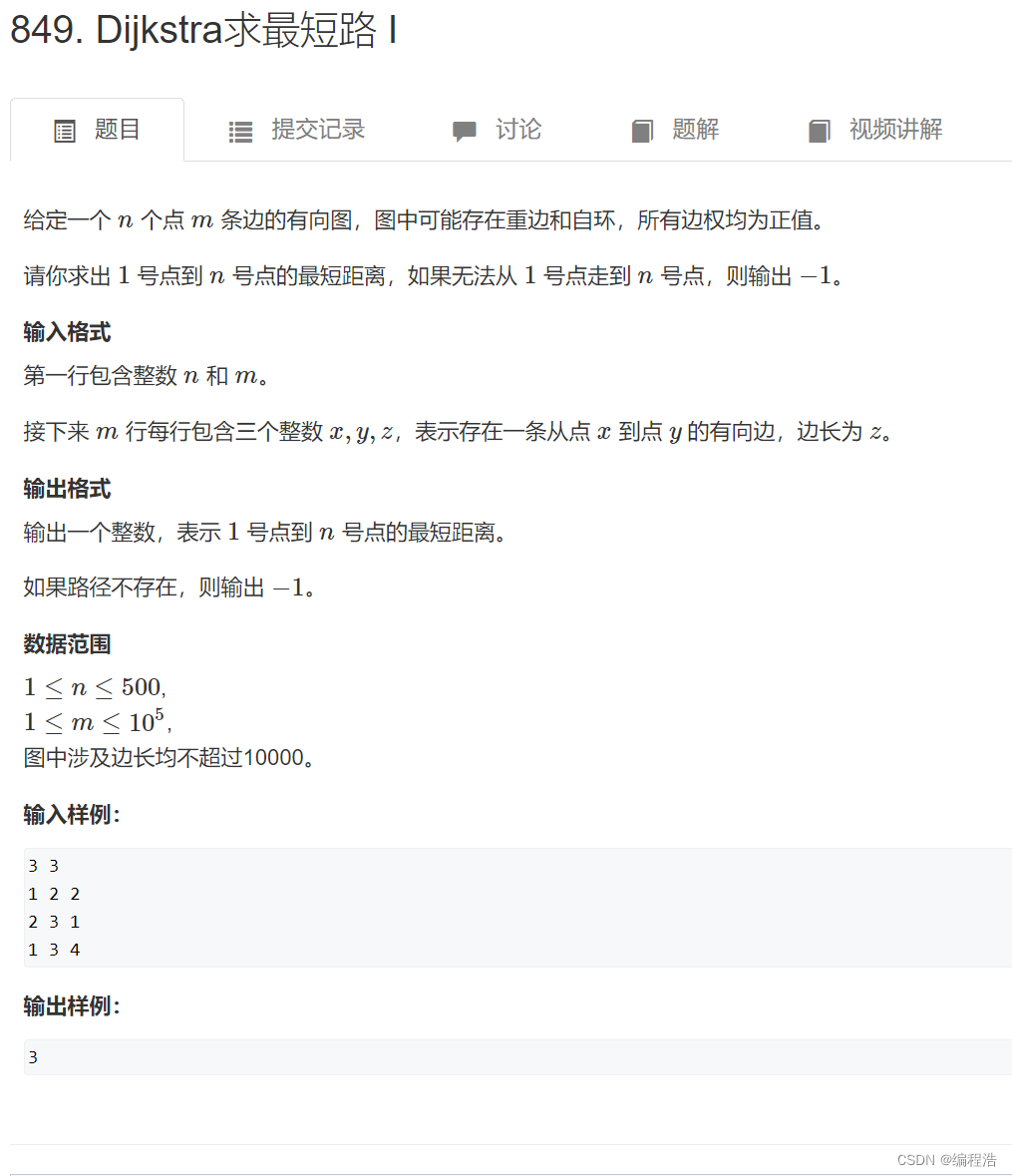
#include <cstring>
#include <iostream>
#include <queue>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int head[N], e[N], ne[N], w[N], idx;
bool st[N];
int dist[N];

void add(int a, int b, int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = head[a];
    head[a] = idx++;
}

int spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    queue<int> q;
    q.push(1);

    st[1] = true;  //判重数组， 队列中有重复的点没有意义

    while (q.size()) {
        int t = q.front();
        q.pop();

        st[t] = false;

        for (int i = head[t]; i != -1; i = ne[i]) {
            int j = e[i];
            if (dist[j] > dist[t] + w[i]) {
                dist[j] = dist[t] + w[i];
                if (!st[j]) {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    if (dist[n] == 0x3f3f3f3f) {
        return -1;
    }
    return dist[n];
}

int main()
{
    cin >> n >> m;

    memset(head, -1, sizeof head);

    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }

    int t = spfa();

    if (t == -1) {
        cout << -1 << endl;
    }
    else {
        cout << dist[n] << endl;
    }

    return 0;
}

3. Floyd求最短路

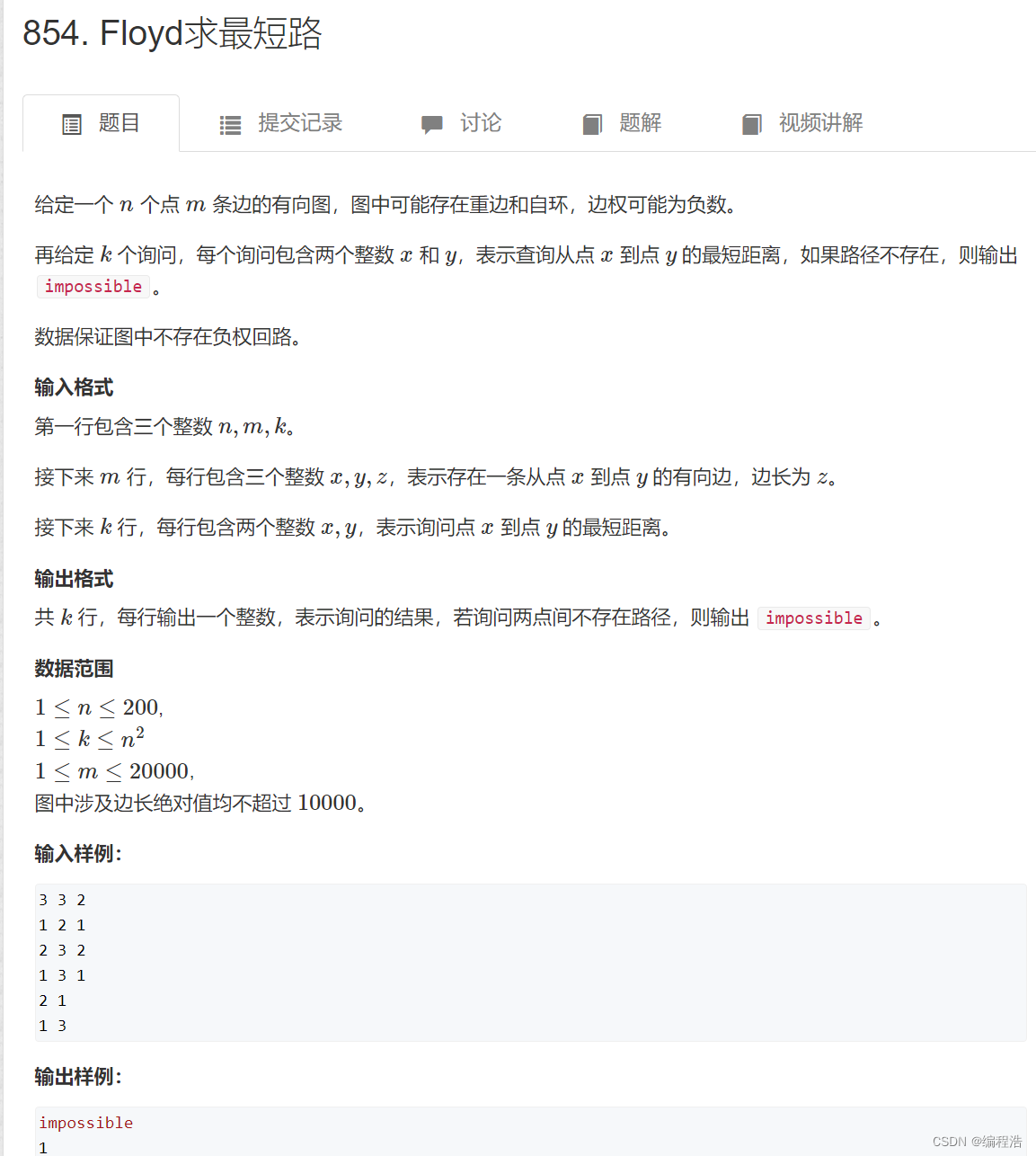
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 210, INF = 0x3f3f3f3f;

int n, m, Q;
int d[N][N];

int main()
{
    scanf("%d%d%d", &n, &m, &Q);
    memset(d, 0x3f, sizeof d);
    for (int i = 1; i <= n; i ++ ) d[i][i] = 0;

    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        d[a][b] = min(d[a][b], c);
    }

    for (int k = 1; k <= n; k ++ )
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

    while (Q -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        int c = d[a][b];
        if (c > INF / 2) puts("impossible");
        else printf("%d\n", c);
    }

    return 0;
}

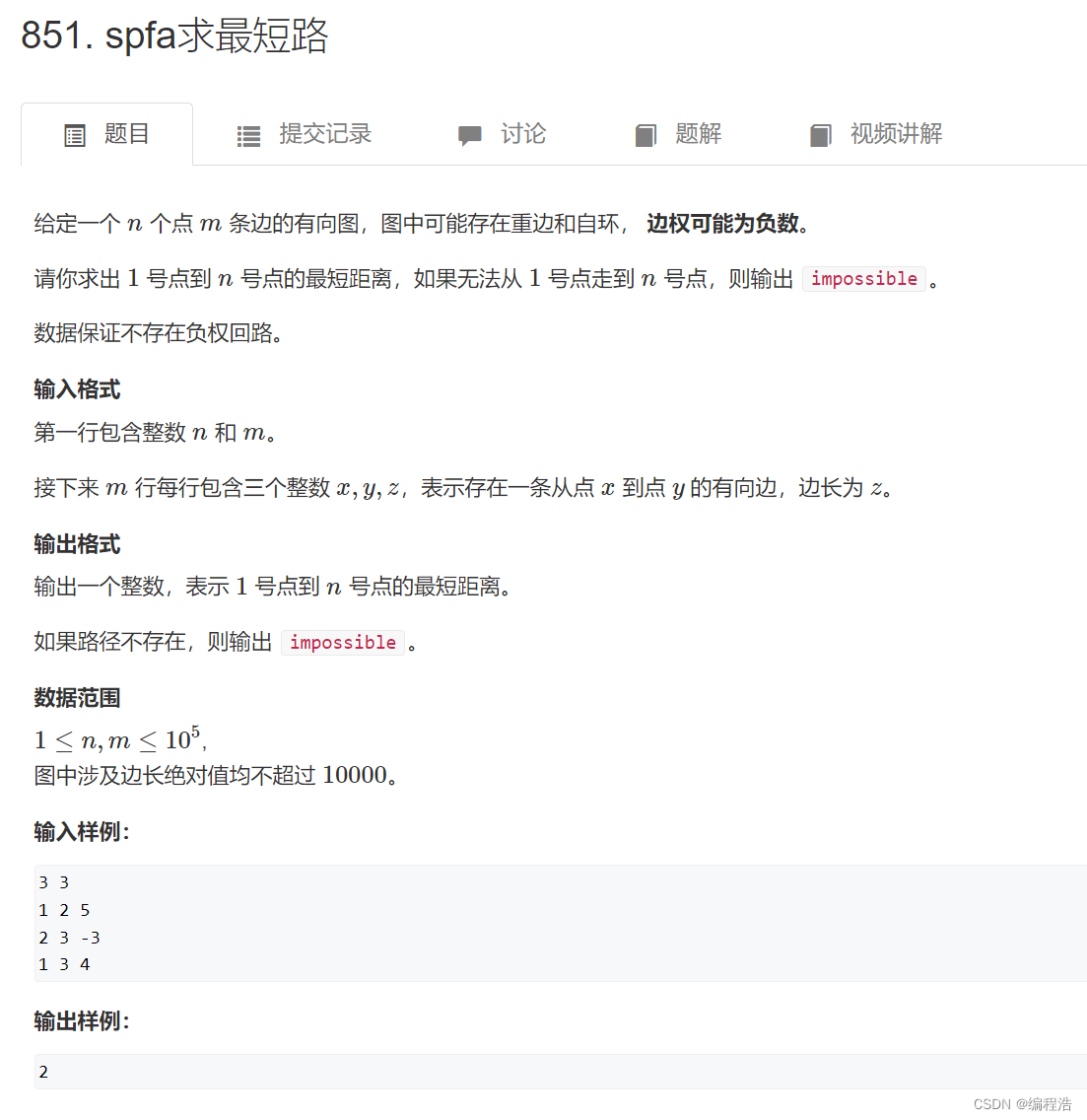
4. spfa求最短路

权值可能为负
所以需要每条路径都走
而不是像dijkstra算法只走一部分

所以spfa算法用普通队列存储即可
并且每个点可能走多次，所以st需要再次false

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 100010;

int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    queue<int> q;
    q.push(1);
    st[1] = true;

    while (q.size())
    {
        int t = q.front();
        q.pop();

        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    int t = spfa();

    if (t == 0x3f3f3f3f) puts("impossible");
    else printf("%d\n", t);

    return 0;
}