文章目录
- 前言
- 1. 一维数组
- 1.1 一维数组的创建
- 1.2 一维数组的初始化
- 1.3 一维数组的访问
- 1.4 一维数组在内存中的存储
- 2. 二维数组
- 2.1 二位数组的创建
- 2.2 二维数组的初始化
- 2.3 二维数组的访问
- 3. 数组越界
- 4. 数组作为函数参数
- 4.1 冒泡排序介绍
- 4.2 冒泡排序函数的设计
- 5. 数组名
- 6. 数组应用实例
前言
- 有时候可能需要保存大量类型一致的数据,如一个班级里边所有学生的成绩,手机通讯录中所有联系人的电话,斐波那契数列的前 100 数……对于这些类型一致、数量庞大的数据,如果使用不同变量来存储,就会让人觉得变成是一件很痛苦的事情。
- 例如,班级中有 50 名学生,那么总共就需要创建 50 个整形变量来存放他们的成绩,如果很不幸,恰好这次又是期末考试,总共考了 5 个科目,那么每一科要创建 50 个变量,总共就需要创建 250 个变量,然后再依次赋值。
#include <stdio.h>
int main()
{
int a1, a2, a3, a4, a5, ..., a50;
int b1, b2, b3, b4, b5, ...,b50;
int c1, c2, c3, c4, c5, ..., c50;
int d1, d2, d3, d4, d5, ..., d50;
int e1, e2, e3, e4, e5, ..., e50;
......
scanf("%d", &a1);
......
scamf("%d", &a50);
scanf("%d", &b1);
......
return 0;
}
- 应该不会有人会写出这种鬼代码出来,所以,C 语言就引入了数组的概念。
1. 一维数组
1.1 一维数组的创建
- 数组就是存储一批同类型数据的地方,定义一维数组的语法格式为:类型 数组名[常量表达式];
int a[6];//定义一个整形数组,总共存放 6 个元素,每个元素都是一个整型
char b[24];//定义一个字符型数组,总共存放 24 个元素,每个元素为一个字符
double c[3];//定义一个双精度浮点型数组,总共存放 3 个元素,每个元素为一个双精度浮点型
- 在定义数组时,需要在数组名后面紧跟一对方括号,其中的数量用来指定数组中元素的个数。
数组的大小
- 在 C99 标准之前,数组的大小必须是常来那个或者常量表达式;
- 在 C99 标准之后,数组的大小可以是变量,为了支持变长数组。
1.2 一维数组的初始化
- 在创建数组的同时对其各个元素进行赋值,称为数组的初始化。
- 数组初始化得方式有很多,主要分为完全初始化和不完全初始化两大类。
完全初始化
- 对数组中得每个元素都进行赋值。
int arr[10] = {1,2,3,4,5,6,7,8,9,10};
不完全初始化
- 只对部分元素进行赋值,其余未被赋值的元素自动初始化为 0。
int arr[10] = {1,2,3};//对前 3 个元素进行赋值,其余 7 个元素系统自动初始化为 0
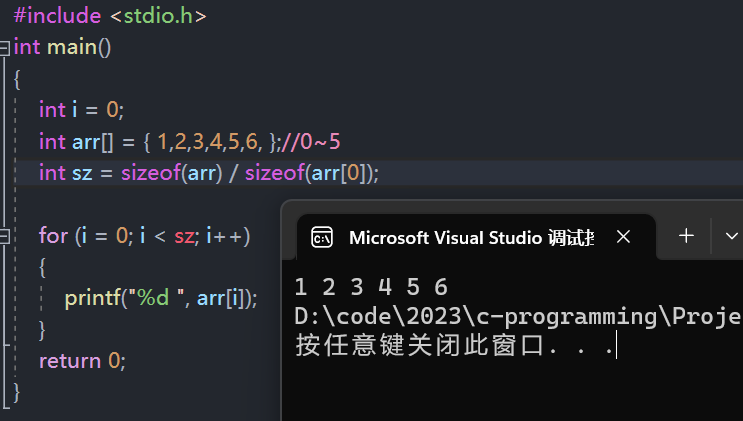
1.3 一维数组的访问
- 对于数组的使用之前介绍了一个操作符:[ ] ,下标引用操作符。它其实就是数组访问的操作符。
- 访问数组的的语法格式为:数组名[下标]
a[0];//访问 a 数组中的第一个元素
b[1];//访问 b 数组中的第二个元素
c[5];//访问 c 数组中的第三个元素
- 注意:在数组中,下标为 0 的才是第一个元素。
计算数组中的元素个数
- 并不是所有的时候都能知道数组的大小,此时就需要让编译器自己去算数组中有多少个元素。
int sz = sizeof(数组名)/sizeof(数组名[首元素下标]);
//计算数组大小,并将结果返回给 sz
- 数组最后一个元素的 下标就是 sz - 1。
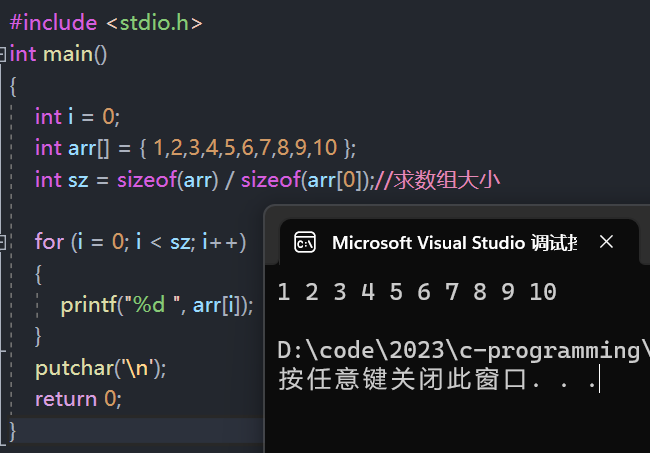
访问数组中的每个元素
- 既然已经知道了数组是通过下标来访问的,并且也知道了如何求数组大小,那么自然也能知道如何访问数组当中的每个元素。
总结
- 数组是使用下标来访问的,下标是从0开始。
- 数组的大小可以通过计算得到。
int arr[10];
int sz = sizeof(arr)/sizeof(arr[0]);
1.4 一维数组在内存中的存储
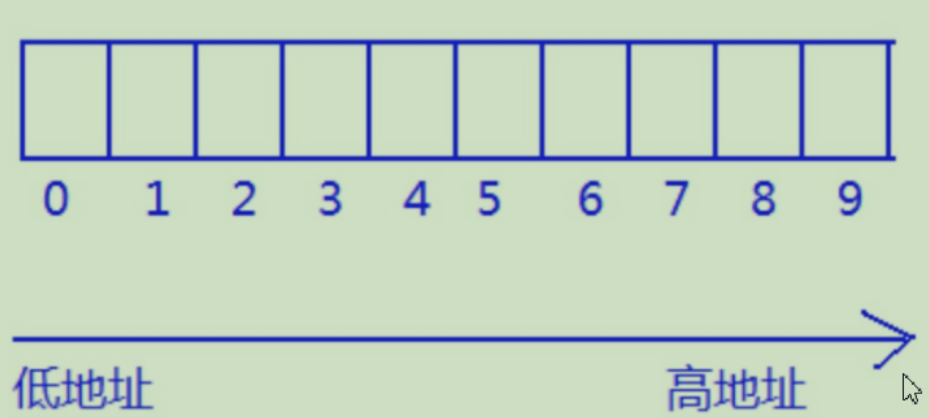
先说结论
- 数组在内存中是连续存放的
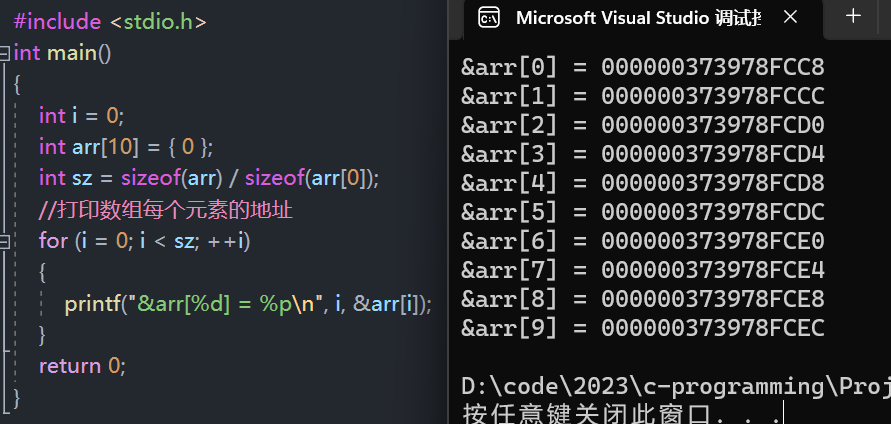
举个栗子
- 每个元素之间的地址都差了 4 个字节
2. 二维数组
- 随着开发的深入,在有些情况下,一维数组难以满足开发的要求,引入二维数组的概念之后,问题就变得简单很多了。
- 二维数组通常也被称之为矩阵,将二维数组写成行和列的形式表示。
2.1 二位数组的创建
- 定义二维数组的方法和一维数组类似,语法格式为:类型 数组名[常量][常量] ;
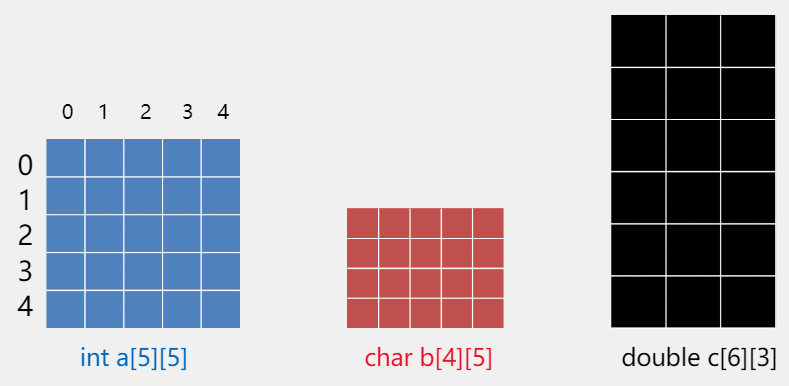
int a[5][5];//5*5,5行5列
char b[4][5];//4*5,4行5列
double c[6][3];//6*3,6行3列
-
二维数组行列的下标都是从 0 开始的。
-
注意:这里需要强调的是几行几列我们是从概念模型上来看的,也就是说,这样来看待二维数组,我们可以更容易理解。但从物理模型上看,无论是二维数组还是更多维的数组,在内存中仍然是以线性的方式存储的。
-
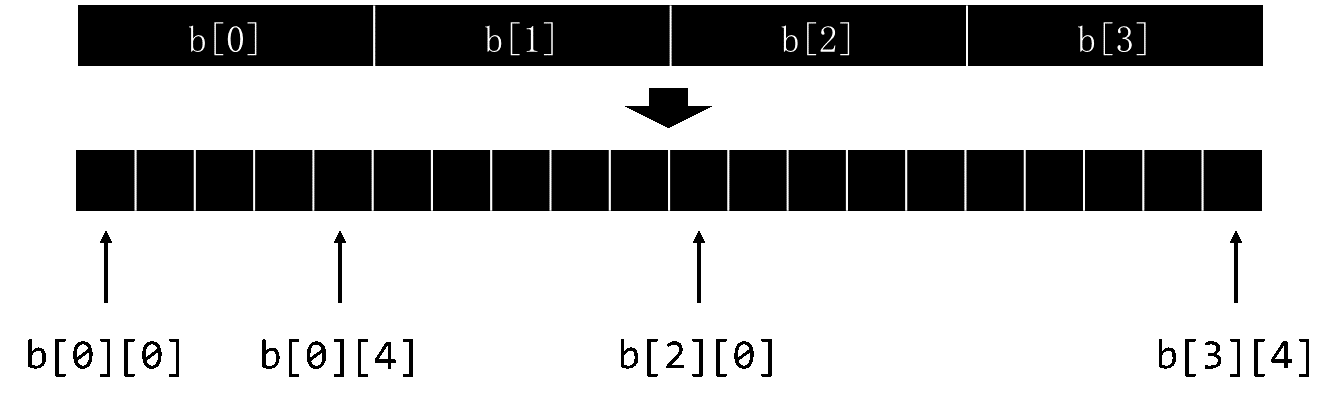
比如,定义了二维数组 int b[4][5];那么 b 在内存中的存放就如下图所示。
- 从图中可以看出,二维数组事实上就是在一维数组的基础上,每个元素存放一个数组。同样道理,三维数组,四维数组都是以同样的方式实现。
- 可以把二维数组理解为,一个一维数组,这个一维数组的每个元素都是一个一维数组。
2.2 二维数组的初始化
二维数组的初始化方式和一维数组类似,下面介绍二维数组的六种初始化方式。
- 二维数组在内存中是线性存放的,因此可以将所有的数据写在一个大括号内。
int a[3][4] = {1,2,3,4,5,6,7,8,9,10,11,12};
//先将第一行的四个元素初始化,再初始化第二行的元素
- 为了更加直观地表示元素的分布,可以用大括号将每一行的元素括起来,会更加清晰。
int a[3][4] = {
{1,2,3,4},
{5,6,7,8},
{9,10,11,12}
};
- 二维数组也可以只对部分元素赋值,这样写是只对各行的第一列元素赋值,其余元素全部初始化为 0。
int a[3][4] = {{1},{5},{9}};
- 如果希望整个二维数组初始化为 0,那么直接在大括号里写一个 0 即可。
int a[3][4] = {0};
- C99 同样增加了一种新特性:指定初始化的元素。这样可以只对数组中得某些指定元素进行初始化赋值,而未被赋值的元素自动被初始化为 0。
int a[3][4] = {[0][0] = 1,[1][1] = 2,[2][2] = 3};
- 二维数组的初始化也能 “ 偷懒 ”,让编译器根据元素的数量计算数组的长度,但是只有第一维的元素个数可以不写,其他维度必须写上(可以省略行,不能省略列)。
int a[][4] = {{1,2,3,4},{5,6,7,8},{9,10,11,12};
2.3 二维数组的访问
- 访问二维数组中得元素,同样是使用方括号 [ ]。语法格式为 数组名[下标][下标] ;
a[0][0];//访问 a 数组中第一行第一列的元素
b[1][3];//访问 b 数组中第二行第四列的元素
c[3][3];//访问 c 数组中第四行第四列的元素
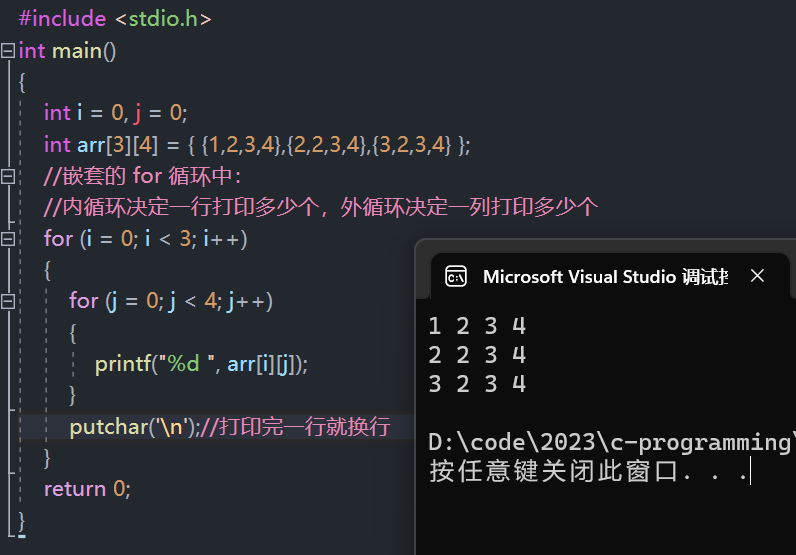
举个栗子
- 将二维数组的所有元素打印到屏幕上。
3. 数组越界
- 在使用数组时,要防止数组下标超出边界。也就是说,必须确保下标是有效的值。
int arr[10];
- 在使用该数组时,要确保程序中使用的数组下标在 0~9 的范围内;
- 因为编译器不会检查出这种错误(但是,一些编译器会发出警告,然后继续编译程序)。
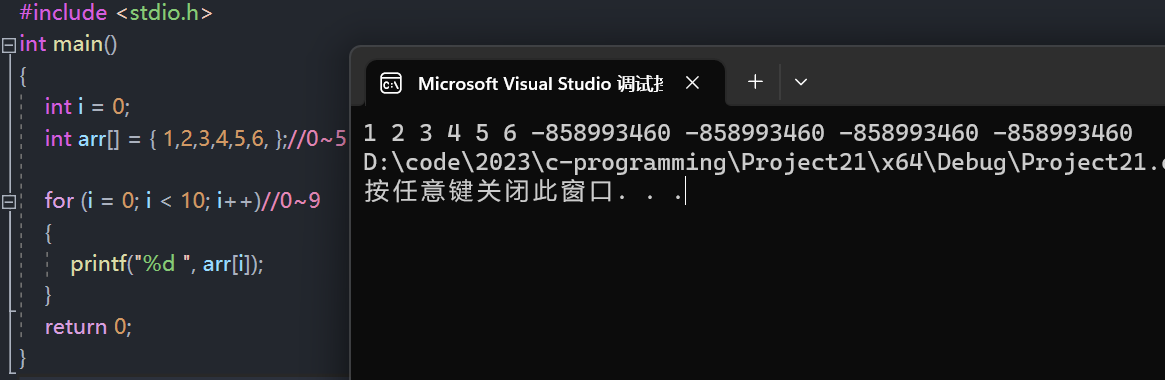
越界访问数组
- 使用越界的数组下标会导致程序改变其他变量的值。
预防数组越界
- 可以使用 sizeof 来让程序自己判断数组的大小,从而避免自己犯迷糊了导致数组越界。
4. 数组作为函数参数
- 往往我们在写代码的时候,会将数组作为参数传个函数;
- 比如:我们要实现一个冒泡排序函数将一个整形数组排序。
4.1 冒泡排序介绍
基本思想
- 将两两相邻的元素进行比较,小的放左边,大的放右边(交换数据),按照递增来排序,不满足条件就交换数据,满足则不管。
- 将某个数排到最终的位置,这一轮叫一趟冒泡排序。
- 每一趟冒泡排序可以让 1 个元素走到最终位置.
- 对于 6 个元素要进行 5 趟冒泡排序。
- n 个元素要进行 n - 1 趟冒泡排序。
冒泡排序过程(升序)
初始:21,25,49,25*,16,08 ;n = 6。
- 第 1 趟
- 第 1 趟结束后:21,25,25*,16,08,49。
- 第 1 趟结束之后,49 已经有序了,那么下一趟就不用管它了。
- 第 2 趟
- 第 2 趟结束后:21,25,16,08,25*,49。
- 继续下一趟,每一趟增加一个有序元素。
- 第 3 趟结果:21,16,08,25,25*,49。
- 第 4 趟结果:16,08,21,25,25*,49。
- 第 5 趟结果:08,16,21,25,25*,49。
冒泡排序算法总结
- n 个元素,总共需要 n - 1 趟冒泡排序。
- 第 i 趟需要比较 n - i - 1 次。
4.2 冒泡排序函数的设计
1. 冒泡排序函数的错误设计
- 错误的使用了数组名传参,在函数体内部利用数组名求数组元素个数。
//冒泡排序函数的错误设计
#include <stdio.h>
void bubble_sort(int arr[])//arr看似是数组,实则为指针
{
int n = sizeof(arr) / sizeof(arr[0]);
//数组名传参传过来的实际是个指针,32 位系统下指针为 4 个字节;
//所以 n 的结果为 4 / 4 = 1,元素个数都算不对,下面的代码更不用说了
//算出 n = 1 的话,n-1=0,循环压根就没进去,自然不会排序了
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - 1 - i; j++)
{
int tmp = 0;
if (arr[j] > arr[j + 1])//交换数据
{
tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
}
int main()
{
int i = 0;
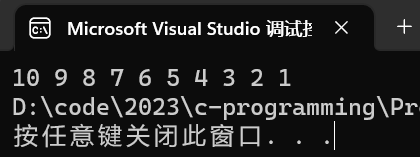
int arr[] = { 10,9,8,7,6,5,4,3,2,1 };
bubble_sort(arr);//传过去的是数组首元素的地址
for (i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
printf("%d ", arr[i]);
}
return 0;
}
2. 冒泡排序函数的正确设计
- 在函数体外部求出数组元素个数,然后将元素个数传参给函数。
//冒泡排序函数的正确设计
#include <stdio.h>
void bubble_sort(int arr[], int n)
{
for (int i = 0; i < n-1; i++)//n 个元素,总共需要进行 n-1 趟冒泡排序
{
for (int j = 0; j < n - 1 - i; j++)//每一趟冒泡排序要比较 n-i-1 次
{
int tmp = 0;
if (arr[j] > arr[j + 1])//交换数据
{
tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
}
int main()
{
int i = 0;
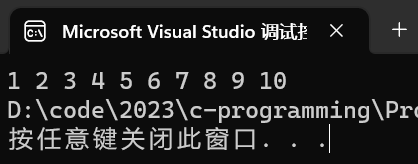
int arr[] = { 10,9,8,7,6,5,4,3,2,1 };
int n = sizeof(arr) / sizeof(arr[0]);
//使用数组名传参的话,如果要用到数组元素个数,必须在主函数中求出结果再传给函数
bubble_sort(arr,n);//数组名传参传过去的是数组首元素的地址
for (i = 0; i <n; i++)
{
printf("%d ", arr[i]);
}
return 0;
}
5. 数组名
绝大多数情况下,数组名是数组首元素的地址,但有两种情况例外。
- sizeof(数组名):这里的数组名表示整个数组,计算的是整个数组的大小。
- &数组名:取出的是整个数组的地址。
#include <stdio.h>
int main()
{
int arr[10] = 0;
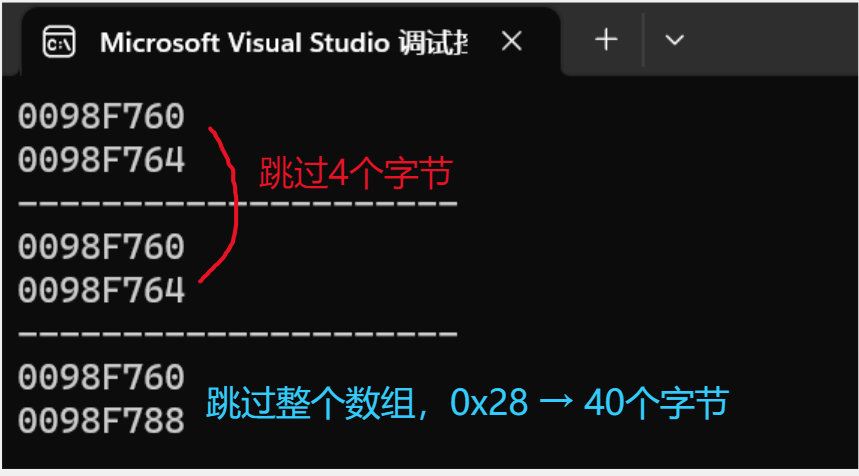
printf("%p\n", arr);//arr 就是首元素的地址
printf("%p\n", arr + 1);//地址+1,跳过一个元素
printf("---------------------\n");
printf("%p\n", &arr[0]);// 取出首元素的地址
printf("%p\n", &arr[0] + 1);//跳过一个元素
printf("---------------------\n");
printf("%p\n", &arr);//整个数组的地址的表现形式也是首元素地址
printf("%p\n", &arr + 1);//但是数组地址+1会跳过整个数组
return 0;
}
二维数组的数组名的理解
- 二维数组的数组也表示首元素的地址,但二维数组的首元素和我们想的有点不太一样。
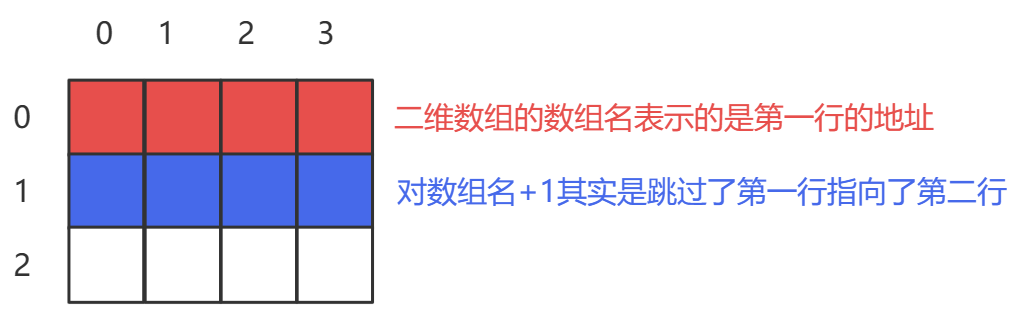
- 二维数组的数组名表示的是第一行的地址。
- 对数组名+1会直接跳过一行。
二维数组行列数的计算
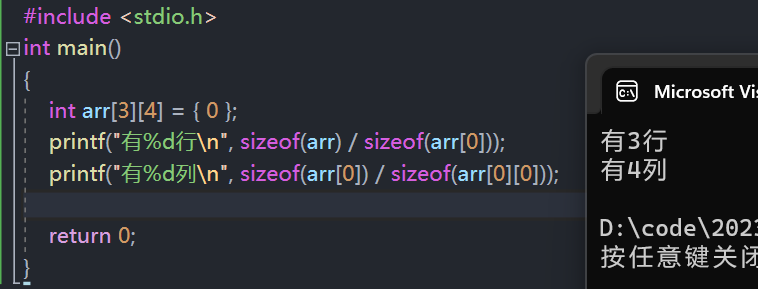
- 计算行数:总数组的大小 / 一行的大小
sizeof(数组名) / sizeof(数组名[0]);
//二维数组第一行的数组名是 数组名[0]
- 计算列数:一行的大小 / 一个元素的大小
sizeof(数组名[0]) / sizeof(数组名[0][0]);
6. 数组应用实例
- 三子棋游戏
- 扫雷游戏





![[TIFS 2023] 用增强压缩感知做安全模型对比联邦学习](https://img-blog.csdnimg.cn/img_convert/bee54a251c0b90c3479a7f063195247e.gif)





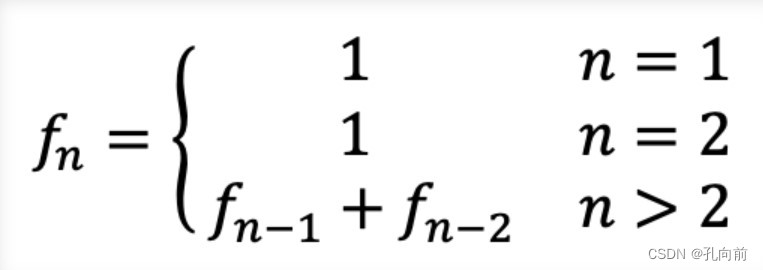

![NSS [NISACTF 2022]babyupload](https://img-blog.csdnimg.cn/img_convert/7716804d9e2703051ba84ea783def604.png)