代码随想录第21天 | 回溯理论基础 77. 组合

回溯理论基础

回溯法解决的问题都可以抽象为树形结构，是的，我指的是所有回溯法的问题都可以抽象为树形结构！

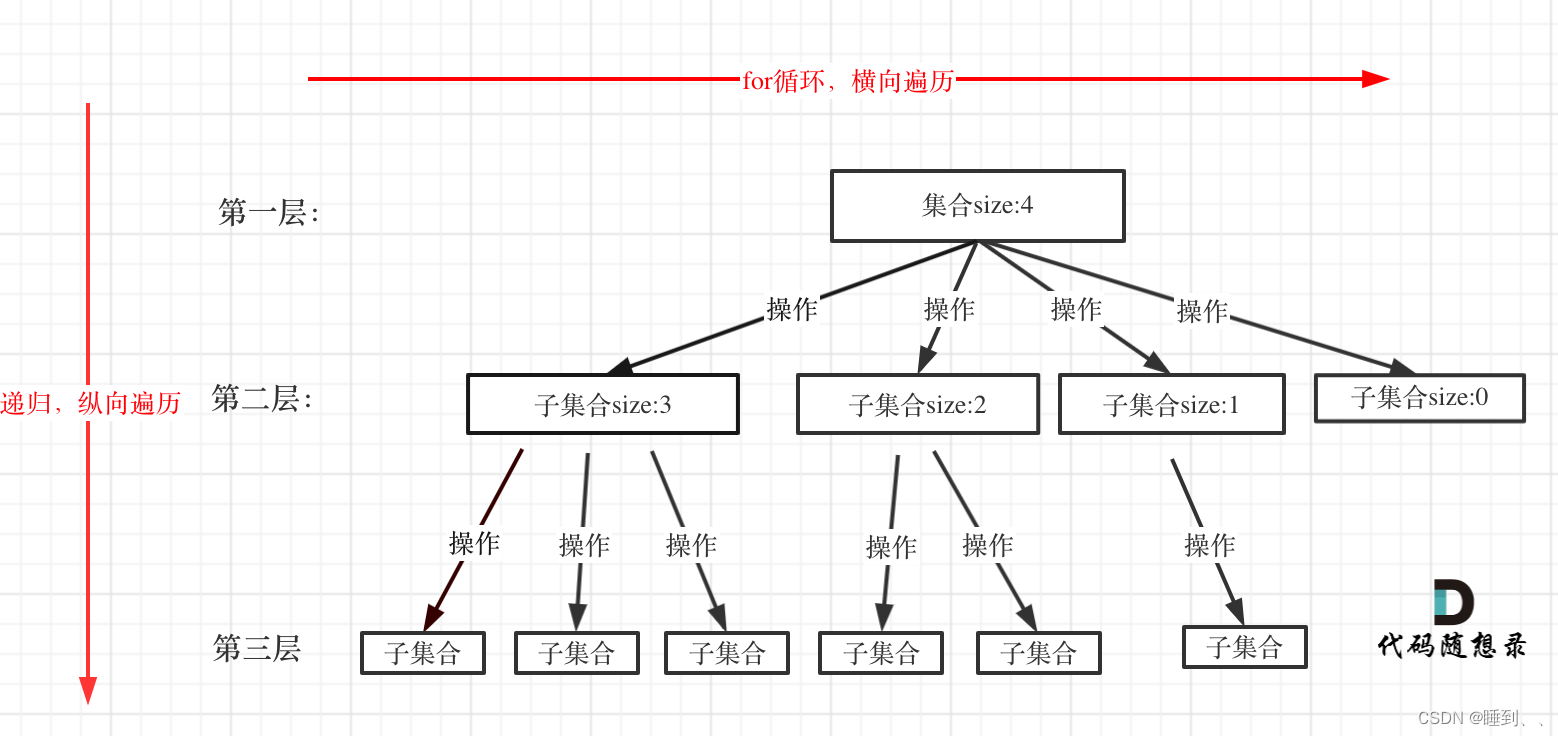
因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。

递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

回溯模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

77.组合

  let road = [];
  let path = [];
  
var combine = function (n, k) {
  road = []  //road会有之前的数据，所以需要每次清空road
  brektraning(n, k, 1);
  return road;
};
  const brektraning = function (n, k, er) {
    if (path.length === k) {  //收割
      road.push([...path]);  //push不能为数组，所以只能先展开
      return;
    }
    for (let i = er; i <= n - (k - path.length) + 1; i++) { //剪枝
      path.push(i);
      brektraning(n, k, i + 1);
      path.pop();
    }
  };