堆排序，即利用堆的思想来进行排序。要实现堆排序，首先要建堆，建堆又分为建大堆和建小堆；然后再一步一步地删除堆的元素来进行排序。

目录

一、堆排序的时间复杂度

二、建堆

向上调整

向下调整

三、堆排序

四、代码实现

向上调整

向下调整

堆排序

---

一、堆排序的时间复杂度

相比冒泡排序，它的时间复杂度为O(N^2)，堆排序的时间复杂度为O(N*logN)。优点就在此。

假如现在要分别对1000个和1000000个数据进行排序，那么

N	冒泡排序	堆排序
1000	1000000	10000
1000000	1E+12	20000000

可见，堆排序的次数更少，更能有效节省时间。

二、建堆

建堆有两种，分别是向上建堆和向下建堆，应该根据需求建大堆或是小堆。

向上调整

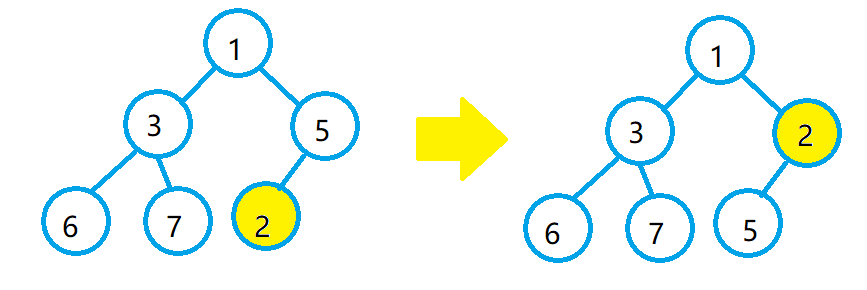
以建小堆为例，2是新插入的数据，让他和父节点5比较，发现父节点比它大，就交换。

然后再和新的父节点1比较，发现新的父节点比它小，就不需要再进行交换了。

再以建大堆为例，这是一个无序的数组：

它们的逻辑结构如下：

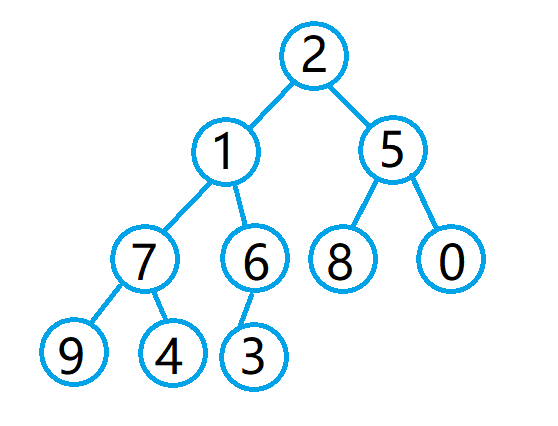
现对它进行向上调整，建大堆，通过调试可以发现，数组元素的值有所改变：

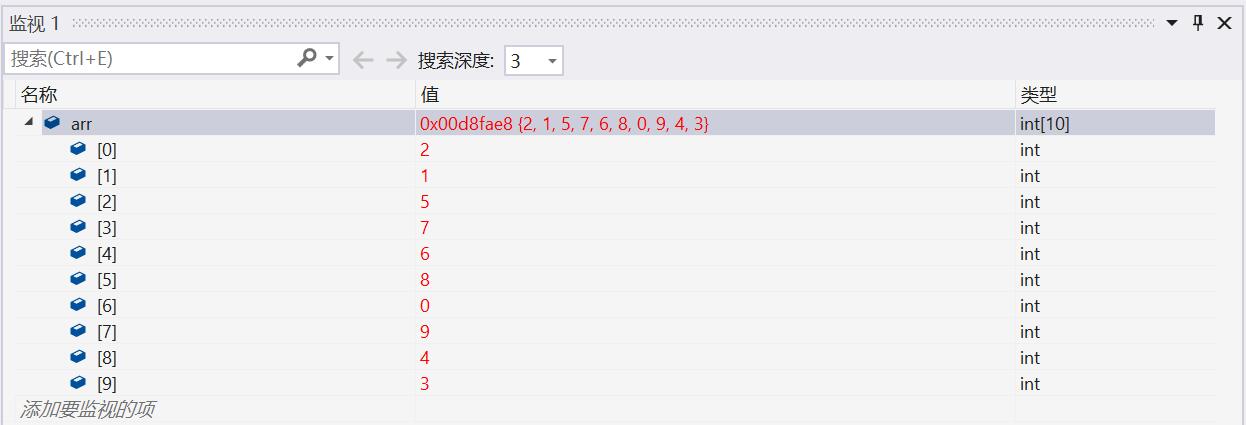
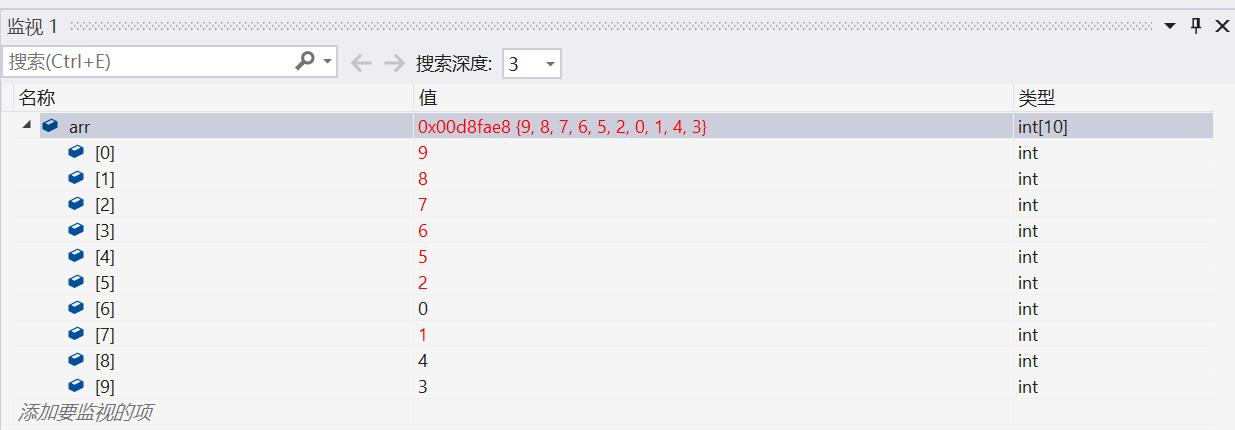
最终，它的逻辑结构如下：

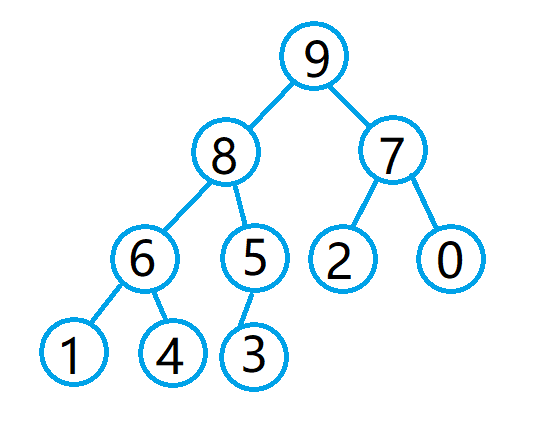
以建小堆为例，向上调整思想如下：

①将要插入的数据与其父节点数据比较

②若子节点数据小于父节点数据，则交换

若子节点数据大于父节点数据，则不交换，不需要调整，已经满足堆的结构

建大堆只是比较大小有所不同。

向下调整

向下调整的一个重要前提是左右子树必须是堆，如图所示：

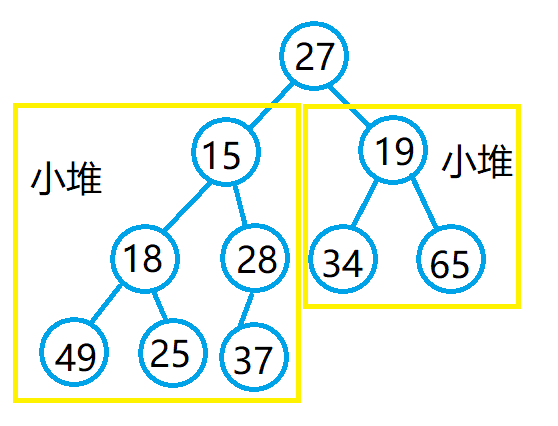
 以建小堆为例：

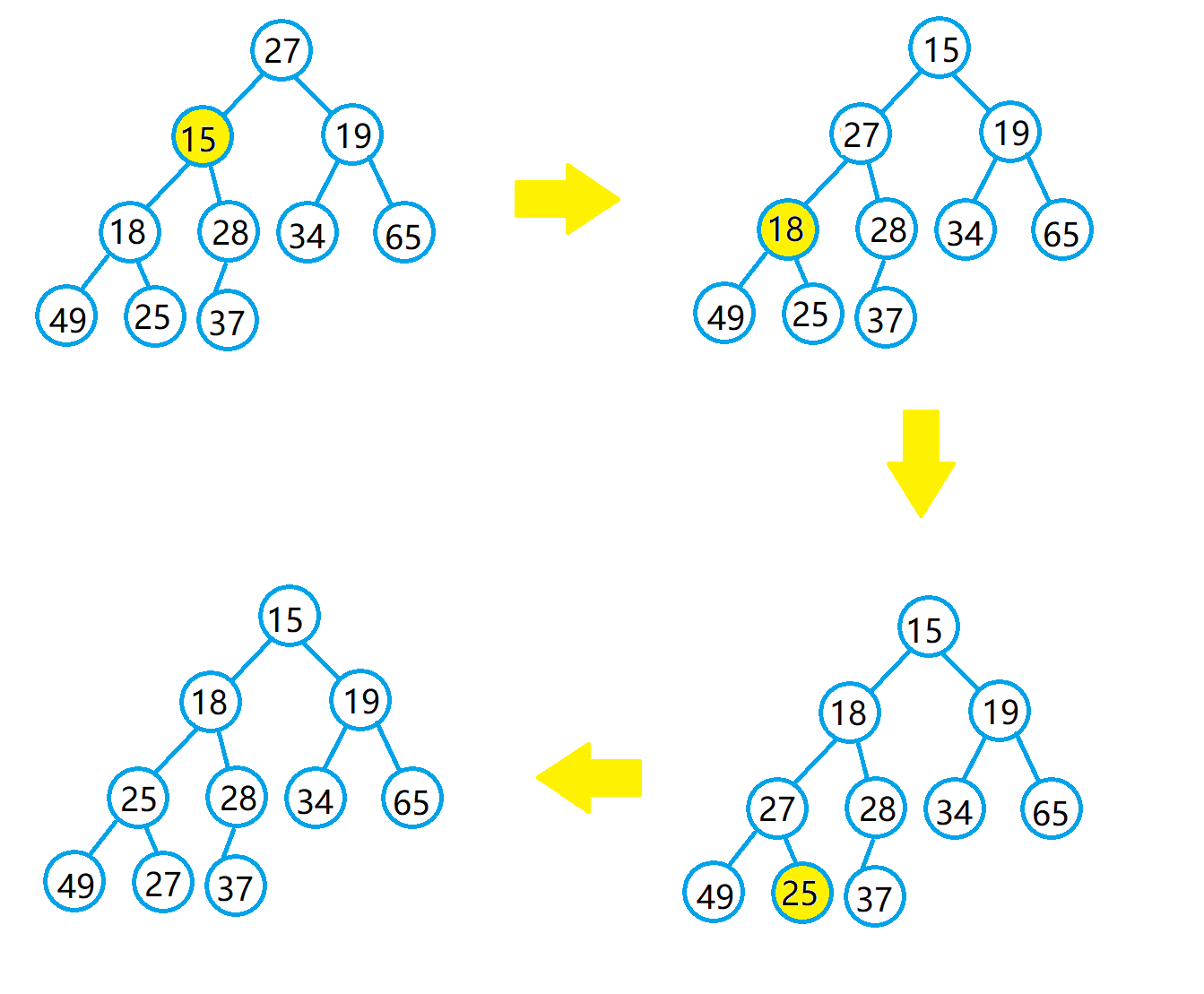
 首先让父节点27和第一个子节点比较大小，发现父节点比子节点大，那么两者交换；

让27和它的第一个子节点比较，发现父节点又比子节点大，那么两者再次交换；

27和它的第一个子节点比较大小，发现第一个子节点比父节点大，那么不交换，让父节点和第二个子节点比较大小，发现父节点比第二个子节点大，那么让两者进行交换。

到了叶子节点了，叶子节点没有子节点，停止比较。最终得到了小堆。

以建成小堆为例，向下调整的思想如下：

①从根节点开始，选出左右孩子节点中值较小的一个

②让父亲与较小的孩子比较

若父亲大于此孩子，那么交换

若父亲小于此孩子，则不交换

③结束条件

1、父亲<=小的孩子则停止

2、调整到叶子节点，（叶子节点特征为没有左孩子，就是数组下标超出了范围，就不存在了）

三、堆排序

堆排序思想如下：

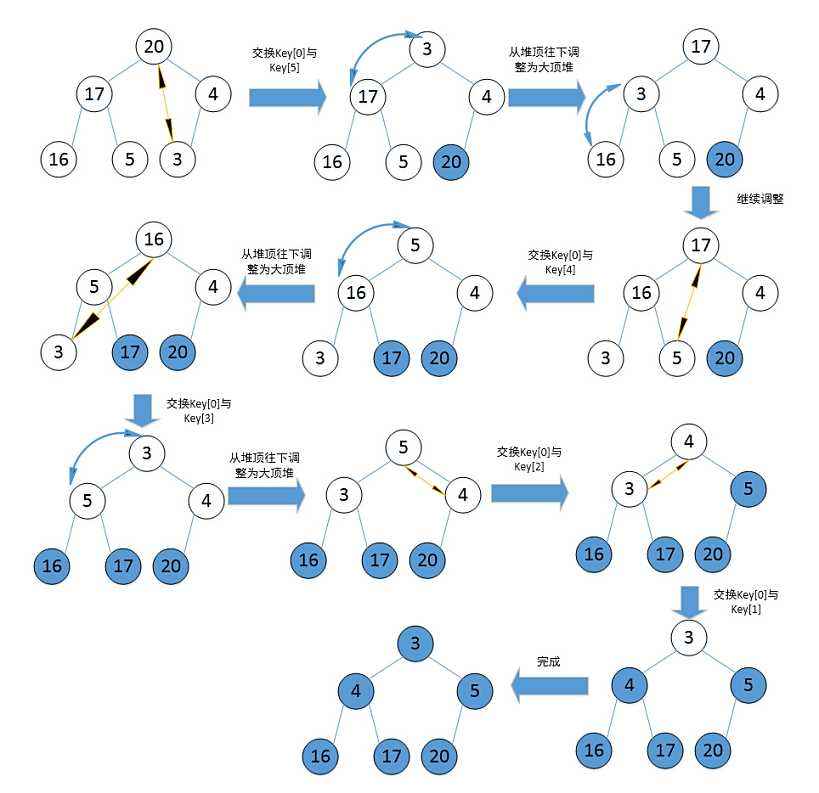
以升序为例，堆排序的思想如下：

①将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。

②将其与末尾元素进行交换，此时末尾就为最大值。

③然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

四、代码实现

向上调整

void AdjustUp(int* a, int child)
{
	int parent = (child - 1) / 2;
	while(parent>=0)
	{
		if (a[parent] < a[child])
		{
			Swap(&a[parent],&a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

向下调整

void AdjustDown(int *a,int n,int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

不论是向上调整还是向下调整，要想建立大堆或小堆，关键在父节点和子节点比较时的符号，可自行修改。

堆排序

void HeapSort(int* a, int n)
{
	// 建堆 -- 向上调整建堆 -- O(N*logN)
	/*for (int i = 1; i < n; ++i)
	{
		AdjustUp(a, i);
	}*/

	// 建堆 -- 向下调整建堆 -- O(N)
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(a, n, i);
	}

	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[end], &a[0]);
		AdjustDown(a, end, 0);
		--end;
	}
}