文章目录
- 一:01背包问题
- (1)题目描述
- (2)解题思路
- (3)完整代码
- 二:分割等和子集(01背包变形)
- (1)题目描述
- (2)解题思路
- (3)完整代码
- 三:完全背包问题
- (1)题目描述
- (2)解题思路
- (3)完整代码
一:01背包问题
(1)题目描述
给你一个可装载重量为 W 的背包和 N 个物品,每个物品有重量和价值两个属性。其中第 i 个物品的重量为 wt[i],价值为 val[i],现在让你用这个背包装物品,最多能装的价值是多少?

举个简单的例子,输入如下:
N = 3, W = 4
wt = [2, 1, 3]
val = [4, 2, 3]
算法返回 6,选择前两件物品装进背包,总重量 3 小于 W,可以获得最大价值 6
(2)解题思路
①:考虑状态和选择是什么
- 状态:由于物品不断装入背包,所以状态有两个,分别为背包容量和可选择的物品
- 选择:对于每件物品,你的选择就是要么装进背包要么不装进背包(也就是0和1)
伪代码如下

②:明确table数组定义:状态有两个,所以要定义成一个二维表。table[i][w]表示,对于前i个物品,当前背包的容量为w,此种情况下可以装入的最大价值为table[i][w]
- 例如:
table[3][5] = 6,其含义为对于给定的一系列物品中,若只对前 3 个物品进行选择,当背包容量为 5 时,最多可以装下的价值为 6 - 最终返回:
table[N][W] - 最简单情况:没有物品或背包没有空间时,能装的最大价值为0,即
table[0][...]=table[...][0]=0
伪代码如下

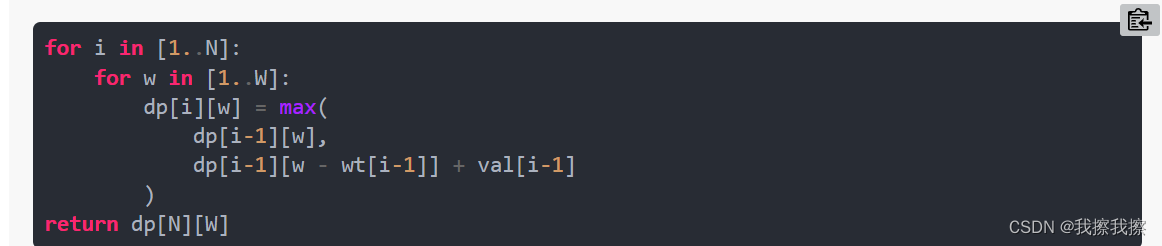
③:根据选择,思考转移的逻辑:也即如何把选择用代码描述出来
- 如果没有把第
i个物品放在背包:很显然,既然没有把第i个放进去,那么价值量不会增加,状态也不会变化,也即table[i][w]==table[i-1][w] - 如果把第
i个物品放入了背包:既然放入了背包,那么此状态的容量一定会减少wt[i],而价值则会增加val[i],因此dp[i][w]==dp[i-1][w-wt[i-1]]+val[i-1]
需要注意的是i是从1开始的,因此val和wt的索引中i-1表示第i个物品。所以dp[i][w]==dp[i-1][w-wt[i-1]]+val[i-1]表示如果把第i个物品装入了,就要寻找剩余重量w-wt[i-1]限制下的最大价值,加上第i个物品的价值val[i-1]
伪代码如下
(3)完整代码
int knapsack(int W, int N, vector<int> &wt, vector<int> &val){
//状态有两个,所以建一个二维数组,注意让其索引从1开始
//最简单情况:table[0][....]=table[....][0] = 0,表示没有物品或背包没有空间时,能装的价值为0
vector<vector<int>> table(N+1, vector<int>(W+1, 0));
//填表过程
for(int i = 1; i <= N; i++){
for(int w = 1; w <= W; w++){
//情况1:若果当前背包容量不足以装下这个物品,则不装入,那么table只能继承前一个
//w - wt[i-1]表示如果把重量为wt[i-1]的物品装入后的重量
if(w - wt[i-1] < 0){
table[i][w] = table[i-1][w];
}else{
//情况2:可以装入,那么就选择最大价值
//
table[i][w] = max(
table[i-1][w-wt[i-1]] + val[i-1],
table[i-1][w]
);
}
}
}
return table[N][W];
}
int main(){
int W = 4;
int N = 3;
vector<int> wt ={2, 1, 3};
vector<int> val ={4, 2, 3};
cout << knapsack(W, N, wt, val) << endl;
}

二:分割等和子集(01背包变形)
(1)题目描述
- LeetCode416:分割等和子集
输入一个只包含正整数的非空数组 nums,请你写一个算法,判断这个数组是否可以被分割成两个子集,使得两个子集的元素和相等
举个简单的例子,输入如下
nums = [1,5,11,5]
算法返回 true,因为 nums 可以分割成 [1,5,5] 和 [11] 这两个子集
(2)解题思路
此题可以转化为背包问题去做,背包问题是这样说的
你一个可装载重量为
W的背包和N个物品,每个物品有重量和价值两个属性。其中第i个物品的重量为wt[i],价值为val[i],现在让你用这个背包装物品,最多能装的价值是多少?
故问题转化为:给你一个可装载重量为sum/2的背包和N个物品,每个物品重量为nums[i],现在让你装物品,问是否存在一种装法,可以恰好把背包装满
①:考虑状态和选择是什么
- 状态:由于物品不断装入背包,所以状态有两个,分别为背包容量和可选择的物品
- 选择:对于每件物品,你的选择就是要么装进背包要么不装进背包(也就是0和1)
②:明确table数组定义:状态有两个,所以要定义成一个二维表。table[i][j]=x表示,对于前i个物品,当前背包的容量为j时,若x为true,则说明恰好可以把背包装满,反之若x为false则表示不可以恰好把背包装满
- 例如:
table[3][5] = true,其含义为对于容量为9的背包,如果只用前4个物品,可以有一种方法将背包装满(对本题来说,就是对于给定的集合,如果只对前4个数字进行选择,存在一个子集的和可以恰好凑出9) - 最终返回:
table[元素个数][sum/2] - 最简单情况:,
table[...][0]=true表示背包没有空间时相当于装满了;table[0][...]=false表示没有元素时肯定没办法装满背包
③:根据选择,思考转移的逻辑:也即如何把选择用代码描述出来
- 如果没有把第
i个物品放在背包(没有把nums[i]算入子集):同理,此时取决于上一个状态,即table[i][j]==table[i-1][j] - 如果把第
i个物品放入了背包(把nums[i]算入子集):同理,取决于状态table[i-1][j-nums[i-1]]
(3)完整代码
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for(auto e : nums){
sum += e;
}
//和为奇数时是不可能分开的
if(sum % 2 != 0){
return false;
}
sum /= 2;
int n = nums.size();
//默认全为false
vector<vector<bool>> table(n+1, vector<bool>(sum+1));
for(int i = 0; i <= n; i++){
table[i][0] = true;
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= sum; j++){
if(j-nums[i-1] < 0){
table[i][j] = table[i-1][j];
}else{
table[i][j] = table[i-1][j] || table[i-1][j-nums[i-1]];
}
}
}
return table[n][sum];
}
};
1:牛客-求正数数组的最小不可组成和
牛客
如果按照原生的背包问题可以这样理解:min为最轻物品的质量,sum为所有物品的总质量,假设有一个背包,其容量范围在[min,sum]之间,还有len件不同重量的物品、、、
也即把数组中的数据看作物品的重量,如果这些物品不能填满某个容量(范围为[min,max])的背包,就表示不能组成那个范围的数
class Solution {
public:
/**
* 正数数组中的最小不可组成和
* 输入:正数数组arr
* 返回:正数数组中的最小不可组成和
*/
int getFirstUnFormedNum(vector<int> arr, int len)
{
//范围为[min,sum];
int sum=0,min=arr[0];
int i,j;
for(int i=0;i<len;i++)
{
sum+=arr[i];
min=arr[i] < min ? arr[i] : min;
}
vector<int> dp(sum+1,0);
for(i=0;i<len;i++)
{
for(j=sum;j>=arr[i];j--)//对于背包容量小于物品的直接忽略
{
if(dp[j] < dp[j-arr[i]]+arr[i])//选上了
dp[j]=dp[j-arr[i]]+arr[i];
else//没选上
dp[j]=dp[j];
}
}
//最后只要放入的重量不是那个区间的数肯定就是所求
for(i=min;i<=sum;i++)
{
if(i!=dp[i])
return i;
}
return sum+1;
}
};
三:完全背包问题
(1)题目描述
- LeetCode518:零钱兑换 II
给定不同面额的硬币 coins 和一个总金额 amount,写一个函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个
函数签名如下
int change(int amount, vector<int>& coins);
举个简单的例子,输入如下
amout = 5
coins = [1, 2, 5]
算法返回4,因为共有如下4种方式可以凑出目标金额
5 = 5
5 = 2+2+1
5 = 2+1+1+1
5 = 1+1+1+1+1
(2)解题思路
此题可以转化为背包问题去做,等价描述为
有一个背包,最大容量为
amout,有一系列物品coins,每个物品的重量为coins[i],物品数量无限,请问有多少种方法可以把背包恰好装满?
①:考虑状态和选择是什么
- 状态:由于物品不断装入背包,所以状态有两个,分别为背包容量和可选择的物品(每个物品可以重复选择)
- 选择:对于每件物品,你的选择就是要么装进背包要么不装进背包(也就是0和1)
②:明确table数组定义:状态有两个,所以要定义成一个二维表。table[i][j]表示,对于前i个物品(可重复使用),当前背包的容量为j时,有table[i][j]种方法可以装满背包(即若只使用conis中的前i个硬币的面值,若要凑出金额j,有table[i][j]种方法)
- 例如:
table[3][5] = 6,其含义为对于给定的一系列物品中,若只对前 3 个物品进行选择,当背包容量为 5 时,有6种方法可以装满背包 - 最终返回:
table[N][amout],其中N为conis数组大小 - 最简单情况:
table[0][....]=0(不使用任何硬币面值,自然无法凑出);table[...][0]=1(如果凑出的目标金额为0,那么唯一做法就是什么都不做)
③:根据选择,思考转移的逻辑:也即如何把选择用代码描述出来
- 如果没有把第
i个物品放在背包(也即不使用coins[i-1]这个面值的硬币):很显然,状态也不会变化,也即table[i][j]==table[i-1][j] - 如果把第
i个物品放入了背包(也即使用了coins[i-1]这个面值的硬币):既然你决定用这个面值的硬币,那么接下来你就应该关注如何凑出金额j-coins[i-1]
(3)完整代码
class Solution {
public:
int change(int amount, vector<int>& coins) {
int n = coins.size();
vector<vector<int>> table(n+1, vector<int>(amount+1));
for(int i = 0; i <= n; i++){
table[i][0] = 1;
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= amount; j++){
if(j - coins[i-1] < 0){
table[i][j] = table[i-1][j];
}else{
table[i][j] = table[i-1][j] + table[i][j-coins[i-1]];
}
}
}
return table[n][amount];
}
};



![[附源码]java毕业设计基于web的健康信息管理系统](https://img-blog.csdnimg.cn/668551f1a4264ecaa918cabeb04cb8d9.png)