一、概览

主成分分析（Principle Component Analysis，PCA）算法属于数据降维算法里面的一种。数据降维算法的主要想法是从高维度数据中找到一种结构，这种结构蕴含了数据中的大部分信息，从而将高维数据降维到低维数据，方便观察、可视化与后续处理。准确地说，PCA算法是在较低维空间中寻求原始数据最准确的数据表示。

二、PCA算法在2维上的一个例子

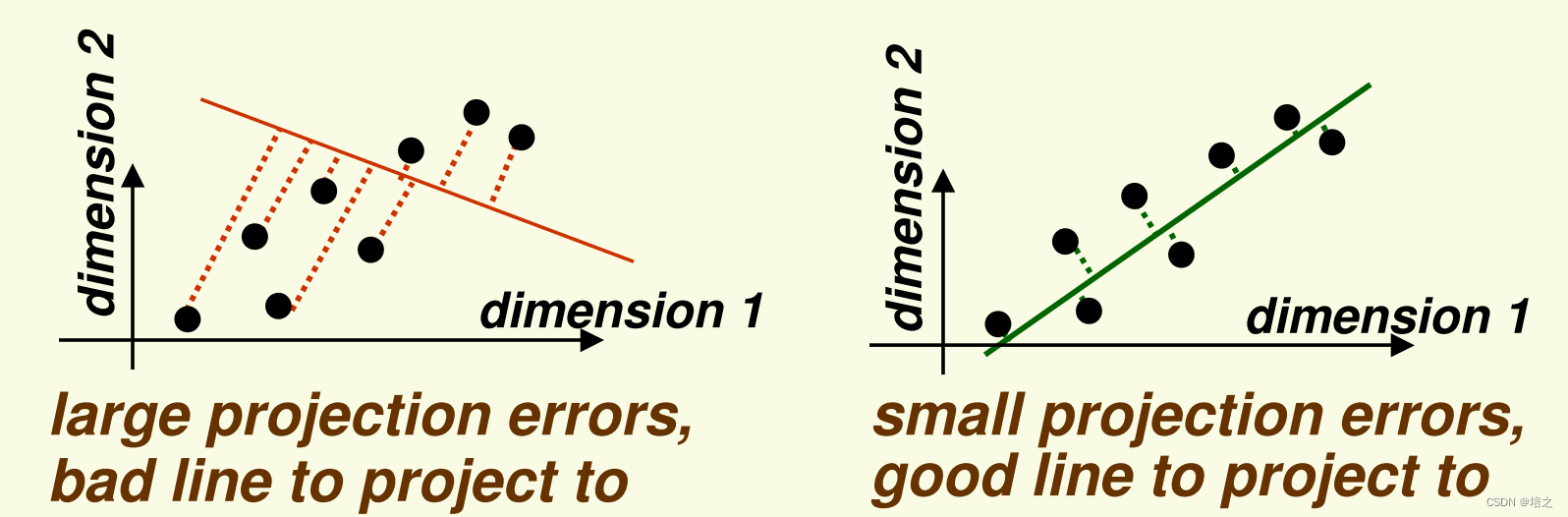
图一展示将数据 $\mathbf{x}$ 投影到一维子空间（一条直线，但其实这里说一维子空间有些不严谨，但是不影响理解，后文有说明），以最小化投影误差。投影误差是点到直线的距离（左图是红色虚线，右图是绿色虚线）。
请注意，从图一上观察到，用于投影的直线，右图中的比左图中的好，因为数据 $\mathbf{x}$ 在后者上投影误差更小。
直观上看，用于投影的最小化数据 $\mathbf{x}$投影误差的方向同时就是使得数据 $\mathbf{x}$方差最大的方向。这个在后面的文章会有数学推导证明。

图 1:

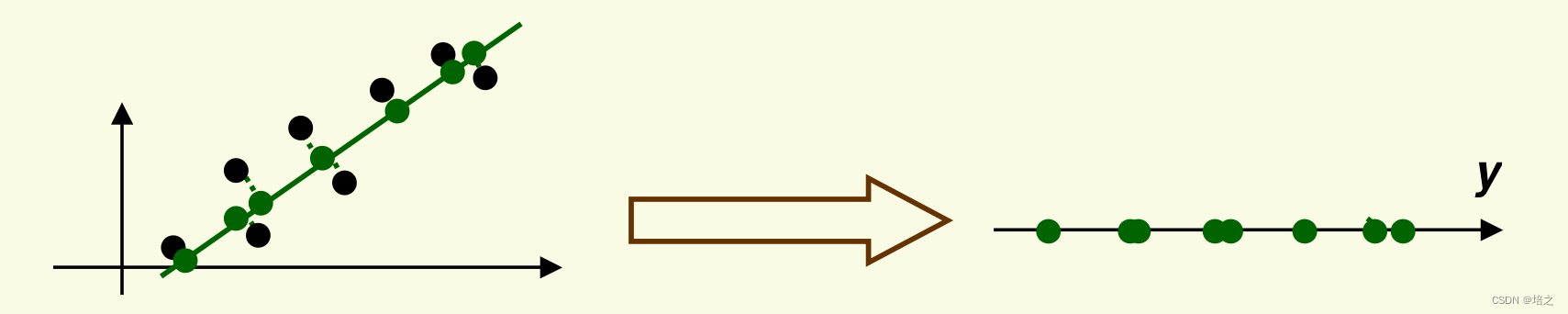
选取图一右侧的直线作为投影直线。数据投影到投影线上后的结果如图2右侧所示。

• 请注意，投影得到的新数据 $\mathbf{y}$ 与旧数据 $\mathbf{x}$ 在投影方向(绿色直线)方向上具有相同的方差。
• PCA 保留数据中最大的方差。 我们将证明这个结论，目前这只是 PCA 将做什么的直觉。

图 2:

为推导PCA算法需要的线性代数知识准备

设 $\mathbf{V}$ 为 $d$ 维 线性空间，$\mathbf{W}$ 为 $\mathbf{V}$ 的 $k$ 维线性子空间。
我们总能找到一组 $d$ 维向量 { e 1 , e 2 , … , e k } \{\mathbf {e_1,e_2,…,e_k}\} {e1​,e2​,…,ek​}，它形成 $\mathbf{W}$的一组正交基 。

• $<{\mathbf{e}}_{\mathbf{i}},{\mathbf{e}}_{\mathbf{j}}>$ = 0, 如果 $i$ 不等于 $j$ ， 注意 $<\ast ,\ast >$ 表示向量内积
• $<{\mathbf{e}}_{\mathbf{i}},{\mathbf{e}}_{\mathbf{j}}>$ = 1, 如果 $i$ 等于 $j$
  则，在$\mathbf{W}$空间中的任何一个向量，都可以表示为
  $${\alpha }_1{\mathbf{e}}_1+{\alpha }_2{\mathbf{e}}_2+\dots {\alpha }_k{\mathbf{e}}_k=\sum _{i=1}^k{\alpha }_i{\mathbf{e}}_i$$
  其中 $${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_k$$ 是标量系数。

回想一下在线性空间中线性子空间的定义，子空间 $\mathbf{W}$ 必须要包含零向量，即它穿过原点。但是图2的投影直线并不穿过原点。所以

后续所有内容都需要投影到子空间 $\mathbf{W}$， 因此我们需要平移所有内容，包括点跟线，使得投影直线过原点。

图 3:

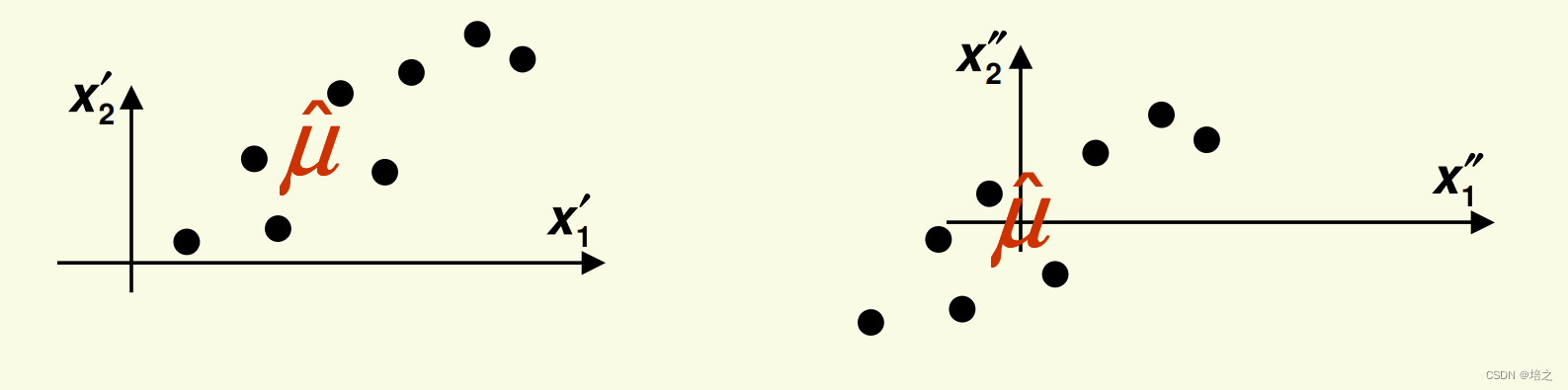
这可以通过每个样本先减去样本均值来实现：
$$\hat{\mu }=\frac{1}{n}\sum _{i=1}^n{\mathbf{x}}_{\mathbf{i}}$$
$${\mathbf{x}}_{\mathbf{i}}:={\mathbf{x}}_{\mathbf{i}}-\hat{\mu },i=1,\dots ,n$$

得到的新的样本数据的均值为0。
事实，我们所作的是改变了坐标系。

图 4:

协方差

当然，数据需要中心化，也可以从协方差角度理解：

为什么数据需要中心化？

是为了 下面这个表达式是协方差矩阵
$$\frac{1}{n-1}\mathbf{X}{\mathbf{X}}^{T}or\frac{1}{n-1}{\mathbf{X}}^T\mathbf{X}$$
上面两个式子转置符号前后位置跟 $\mathbf{X}$ 每一行是一个随机变量，还是每一列是一个随机变量相关。
协方差矩阵的维度是 $d\times d$，注意$d$ 是随机变量的数目，即属性的数目。跟样本的数目要区分开。

参考文献

Introduction to Statistical Machine Learning
Lecture 2
Anders Eriksson
School of Computer Science
University of Adelaide, Australia