题目
题目1
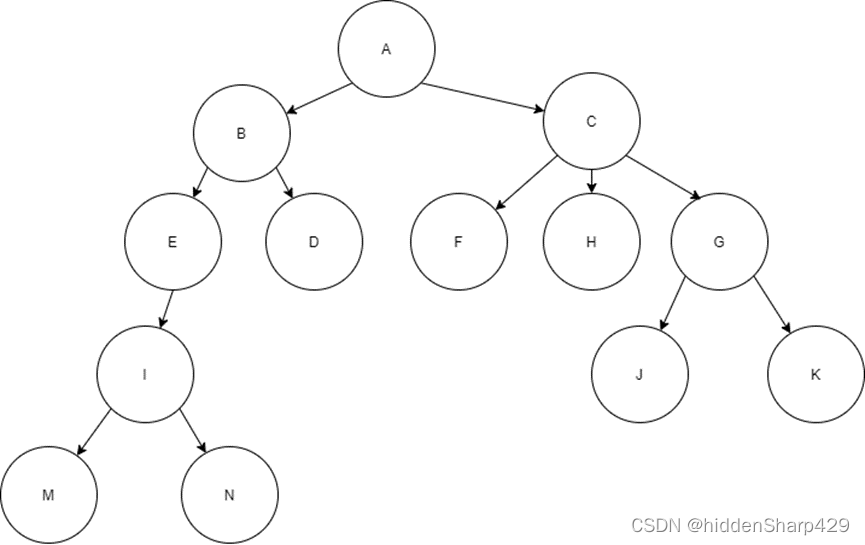
知一棵树边的集合为
<
I
,
M
>
,
<
I
,
N
>
,
<
E
,
I
>
,
<
B
,
E
>
,
<
B
,
D
>
,
<
A
,
B
>
,
<
G
,
J
>
,
<
G
,
K
>
,
<
C
,
G
>
,
<
C
,
F
>
,
<
H
,
L
>
,
<
C
,
H
>
,
<
A
,
C
>
{<I,M>,<I,N>,<E,I>,<B,E>,<B,D>,<A,B>,<G,J>, <G,K>,<C,G>,<C,F>,<H,L>,<C,H>,<A,C>}
<I,M>,<I,N>,<E,I>,<B,E>,<B,D>,<A,B>,<G,J>,<G,K>,<C,G>,<C,F>,<H,L>,<C,H>,<A,C>
请画出这棵树并回答下列问题:
- 哪个是根结点?
- 哪些是叶子结点?
- 哪个是结点G的双亲?
- 哪些是结点G的祖先?
- 哪些是结点G的孩子?
- 哪些是结点E的子孙?
- 哪些是结点E的兄弟?哪些是结点F的兄弟?
- 结点B和N的层次号分别是什么?
- 树的深度是多少?
- 以结点C为根的子树的深度是多少?
该树形状
题目1答案
(1) 根结点:A
(2) 叶子节点:M、N、J、K
(3) 结点G的双亲:C
(4) 结点G的祖先:A、C
(5) 节点G的孩子:J、K
(6) 节点E的子孙:I、M、N
(7) 节点E的兄弟:D;节点F的兄弟:H、G
(8) 结点B和N的层次号分别是:2、5
(9) 树的深度:5
(10) 以结点C为根的子树的深度:2
题目2
一棵度为2的树与一棵二叉树有何区别?
题目2答案
- 结构方面:一棵度为2的树的结点之间没有严格的父子关系,但二叉树中每个结点都有明确的父结点和左右结点。
- 遍历方式:二叉树常用前序、中序、后序遍历,而度为2的树可以用更特殊的遍历方式来遍历,如:从根结点开始,先遍历左子结点、再遍历右子结点、最后递归遍历子树。
题目3
已知一棵度为k的树中有n1个度为1的结点,n2个度为2的结点,…,nk个度为k的结点,问该树中有多少个叶子结点?
题目3答案
度之和:
n
−
1
①
度之和:n-1 ①
度之和:n−1①
度之和:
n
1
+
n
2
∗
2
+
n
3
∗
3..
+
n
m
∗
m
②
度之和:n1+n2*2+n3*3 ..+ nm*m ②
度之和:n1+n2∗2+n3∗3..+nm∗m②
联立解得:
n
0
=
n
2
+
.
.
.
+
(
k
−
1
)
∗
n
k
+
1
联立解得:n0=n2+...+(k-1)*nk+1
联立解得:n0=n2+...+(k−1)∗nk+1
题目4
已知一棵含有n个结点的树中,只有度为k的分支结点和度为0的叶子结点,求该树含有的叶子结点的数目
题目4答案
设叶子结点为
x
个,度为
k
的分支结点为
n
−
x
个
设叶子结点为x个,度为k的分支结点为n-x个
设叶子结点为x个,度为k的分支结点为n−x个
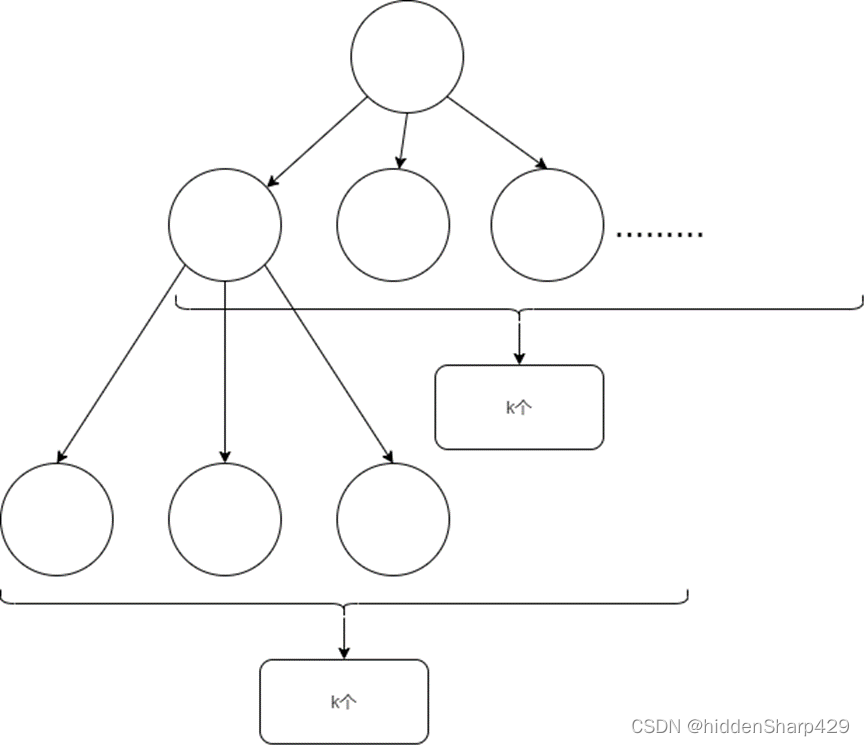
故一共有
1
+
(
n
−
k
)
∗
k
1+(n-k)*k
1+(n−k)∗k个结点(其中1为最顶上的结点也就是根结点)
解:
x
=
n
−
(
n
−
1
)
/
k
解: x= n-(n-1)/k
解:x=n−(n−1)/k
题目5
证明:一棵满k叉树上的叶子结点数n0和非叶子结点数n1之间满足下列关系: n 0 = ( k − 1 ) n 1 + 1 n_0=(k-1)n_1+1 n0=(k−1)n1+1
题目5答案
由于是满k叉树,故只有叶子结点和度为k的非叶子结点,假设一共有n + 1层
n
1
=
(
1
−
k
n
)
/
(
1
−
k
)
n_1=(1-k^n)/(1-k)
n1=(1−kn)/(1−k)
n
0
=
k
n
n_0=k^n
n0=kn
故得证
n
0
=
(
k
−
1
)
n
1
+
1
n_0=(k-1)n1+1
n0=(k−1)n1+1
结束语
因为是算法小菜,所以提供的方法和思路可能不是很好,请多多包涵~如果有疑问欢迎大家留言讨论,你如果觉得这篇文章对你有帮助可以给我一个免费的赞吗?我们之间的交流是我最大的动力!