常微分方程组求解命令与示例

线性常微分方程（组）

ode45

• 4 order 龙格库塔法
• example

odefun = @(t, y) [-2*y(1) + y(2); y(1) - 2*y(2)];
tspan = [0 10];
y0 = [1; 0];
[t, y] = ode45(odefun, tspan, y0);

ode23

•  使用二三阶Bogacki-Shampine方法求解非刚性ODEs

odefun = @(t, y) [-2*y(1) + y(2); y(1) - 2*y(2)];
tspan = [0 10];
y0 = [1; 0];
[t, y] = ode23(odefun, tspan, y0);
plot(t,y)

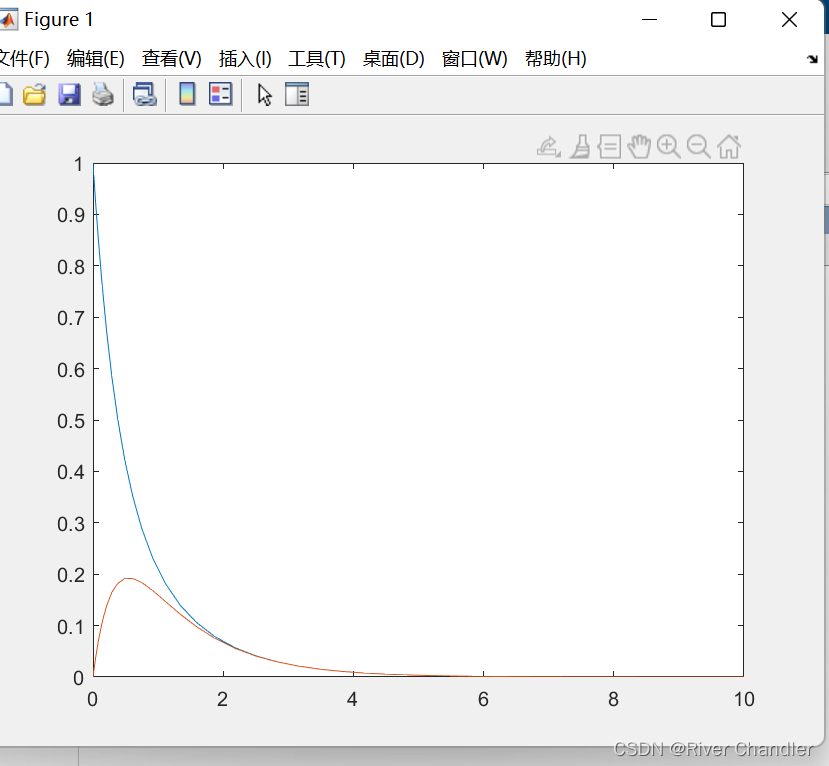
ode15s

• 使用隐式Stiff方法求解刚性ODEs
  • 高频振荡（解在短时间内快速变化）
  • 稳定性（对初始条件和参数的微小变化非常敏感）
  • 刚性矩阵（通常具有较大的条件数，刚性ODEs的数值解法可能会受到数值稳定性的挑战）
  • 通常需要使用隐式方法进行求解
• example

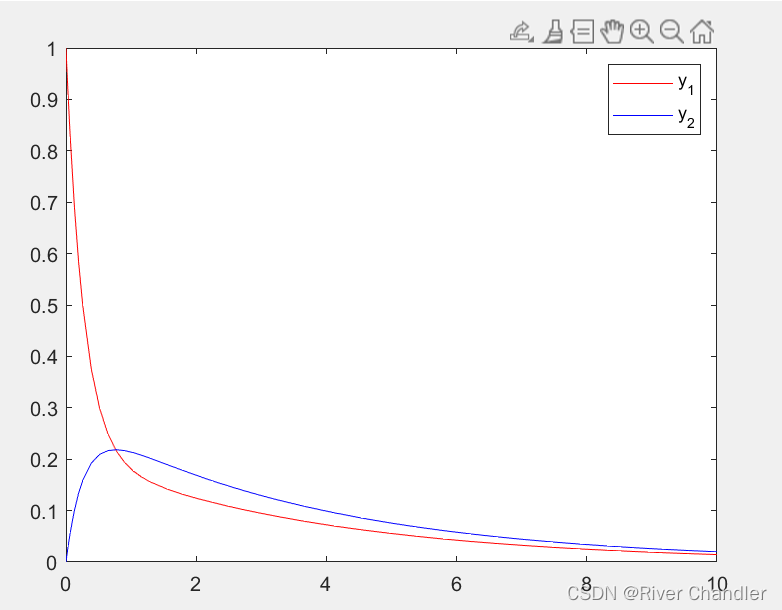
• ode15s的求解结果

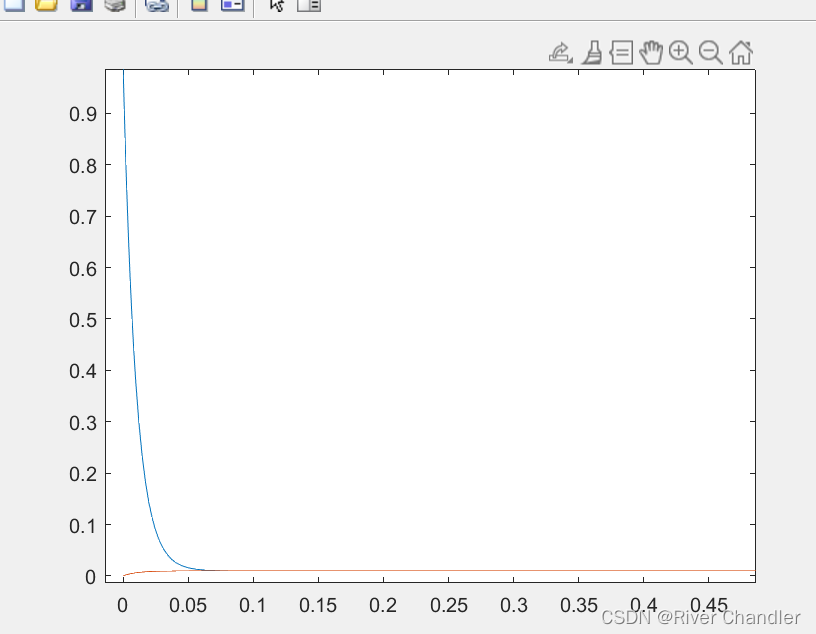
•  ode23的求解结果

•  其实这个例子并不好找，但是有这个程序的存在肯定有他的道理

ode23t

• 变步长的三阶 Rosenbrock 方法

odefun = @(t, y) [-3*y(1) + 2*y(2); y(1) - y(2)];
tspan = [0 10];
y0 = [1; 0];
[t, y] = ode23t(odefun, tspan, y0);
plot(t, y(:, 1), 'r', t, y(:, 2), 'b');
legend('y_1', 'y_2');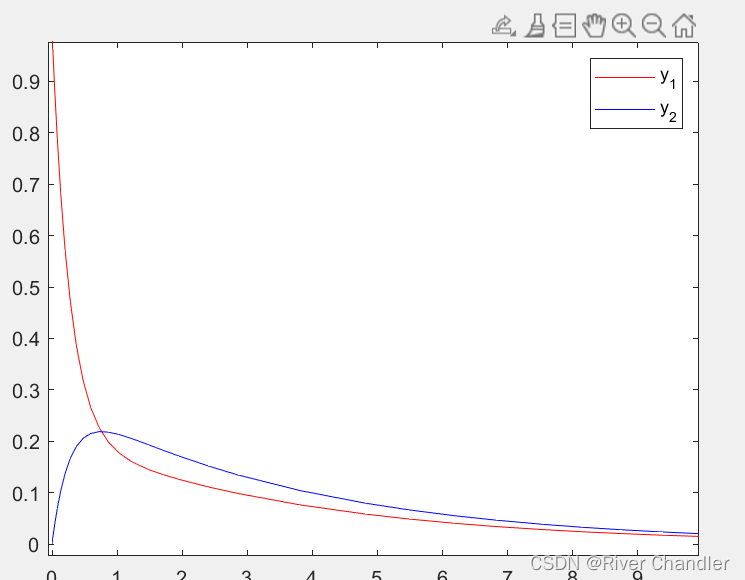

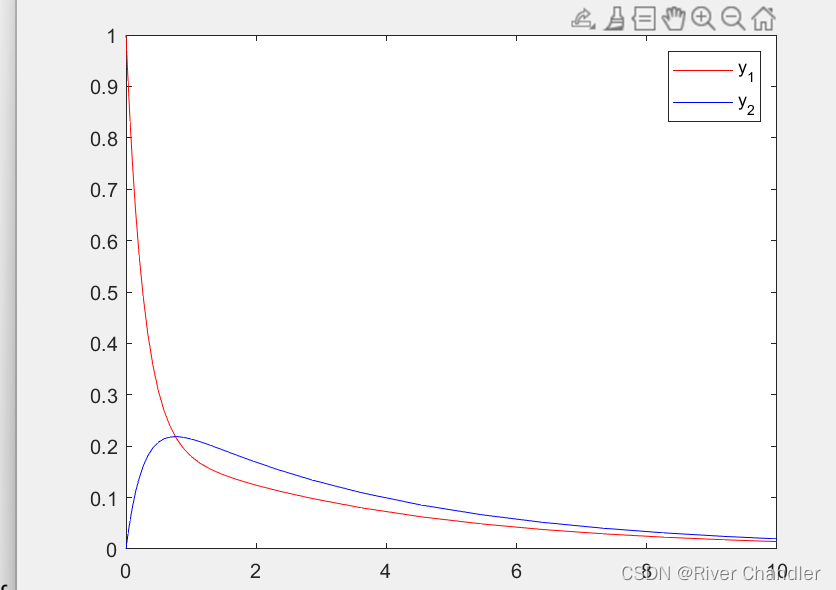
ode23tb

• 使用变步长的三阶 Rosenbrock 方法求解问题，并自动调整步长以保持精度

odefun = @(t, y) [-3*y(1) + 2*y(2); y(1) - y(2)];
tspan = [0 10];
y0 = [1; 0];
[t, y] = ode23tb(odefun, tspan, y0);
plot(t, y(:, 1), 'r', t, y(:, 2), 'b');
legend('y_1', 'y_2');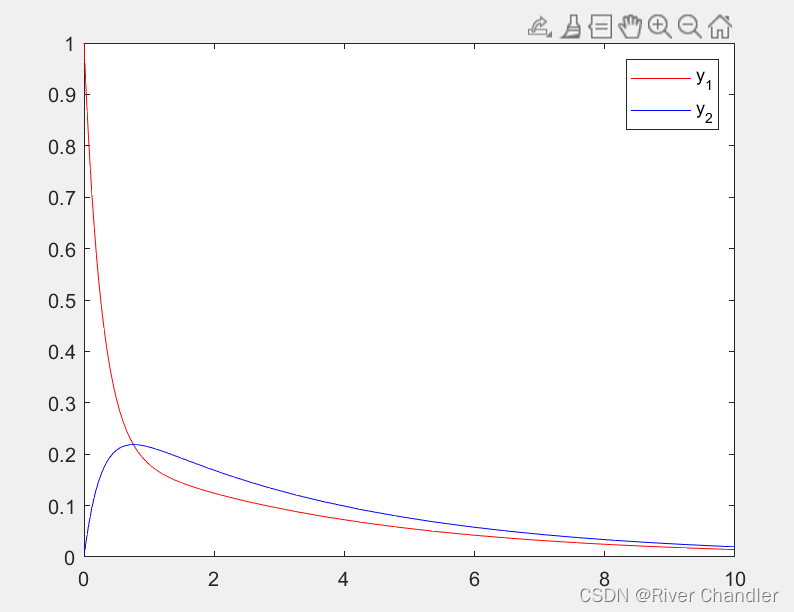

ode113

• 使用 Adams-Bashforth-Moulton 方法求解非刚性问题

ode23s

• 使用二阶 Rosenbrock 方法
  • 适用于解非刚性的常微分方程组

选择最合适的求解器

• 方程组的刚性性质：ode15s
• 方程组的非刚性性质：ode45
• 同时具有刚性和非刚性特性：ode23t
• 阶跃函数或突变：ode23tb

控制求解的精度

• 'RelTol'：相对误差容限，默认值为1e-3
  • 数值解与真实解之间的差异相对于真实解的比例
•  'AbsTol'：绝对误差容限，默认值为1e-6
  • 数值解与真实解之间的差异的绝对值
•  'Refine'：求解结果的细化程度，默认值为4
  • 在数值解过程中所采用的离散化方法的精细程度

odefun = @(t, y) [-3*y(1) + 2*y(2); y(1) - y(2)];
options = odeset('RelTol', 1e-6, 'AbsTol', 1e-8, 'Refine', 10);
tspan = [0 10];
y0 = [1; 0];
[t, y] = ode23tb(odefun, tspan, y0,options);
plot(t, y(:, 1), 'r', t, y(:, 2), 'b');
legend('y_1', 'y_2');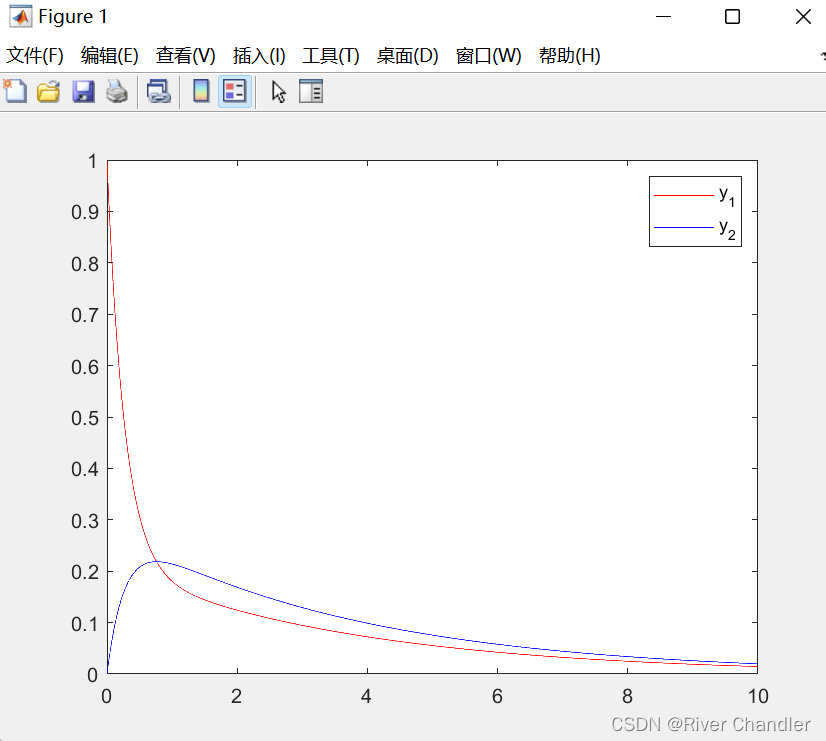

求解误差的评估

Richardson 外推法

• 常见，略

Runge-Kutta-Fehlberg(RKF)方法

• 选择初始步长 h0，并计算每个步长上的解 y_i
• 使用两个不同阶数的Runge-Kutta方法计算两个近似解 y_i^4 和 y_i^5
• 计算误差 error_i = |y_i^5 - y_i^4|
• 根据误差的大小决定是否需要调整步长
• 如果误差小于容忍误差 tolerance，继续使用当前步长进行下一步计算；如果误差大于容忍误差，缩小步长并重新计算

非线性常微分方程（组）

• 我们需要将非线性问题线性化来解决这个问题
• 一般有这几种方法
  • 线性化代换：引入新的变量
  • 幂级数展开法
  • 线性化近似
  • 线性化近似和线性化变换的结合
• 当然，我们的重点不在这里，这太要求技巧了
• 数值积分方法

偏微分方程组求解

• 使用pdetool即可

water begin

窄带和分光片

带宽在 GHz量级甚至MHz量级的窄带光学滤波器逐渐成为不可或缺的核心器件之一。因此在大气激光通信的自适应光学设备中有重要地位。[]

大气激光通信不能够排除天光背景噪声的干扰，因此削弱无用光留下信号光是激光通信的重要步骤之一。

这里列出五种窄带滤光技术，原子共振滤光器，法拉第反常色散滤光器，双折射滤光器，法布里-珀罗滤光器和可调谐声光滤光器。[]

原子共振滤光器是利用原子共振跃迁对信号光进行超窄带滤光，其带宽可达0.001nm。原子共振滤光器的主要原理是信号光进入原子共振滤光器内部后被原子蒸气吸收，原子蒸气经过弛豫，辐射出不同于信号光的特定波长的荧光，从而实现滤光。

这是原子共振滤光器的工作原理图：