问题1：矩阵置零

给定一个 *m* x *n* 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

 解题思路：

1.先遍历一遍矩阵，将元素为0的行和列都标记为true
2.再遍历一遍矩阵，将标记为true的行和列的元素都置为0

源代码如下：

class Solution {
public:
    
    void setZeroes(vector<vector<int>>& matrix) {
        int m=matrix.size();
        int n=matrix[0].size();
        vector<bool> row(m),col(n);//定义行和列的标记，类型为bool类型
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                //遍历矩阵，发现元素为0，则将该元素所在的行和列标记为true
                if(matrix[i][j]==0)
                {
                    row[i]=col[j]=true;
                }
            }
        }
        //将所有标记为true的元素置为0
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(row[i]||col[j])
                {
                    matrix[i][j]=0;
                }
            }
        }
    }
};

问题2：搜索二维矩阵

给你一个满足下述两条属性的 m x n 整数矩阵：

每行中的整数从左到右按非递减顺序排列。 每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

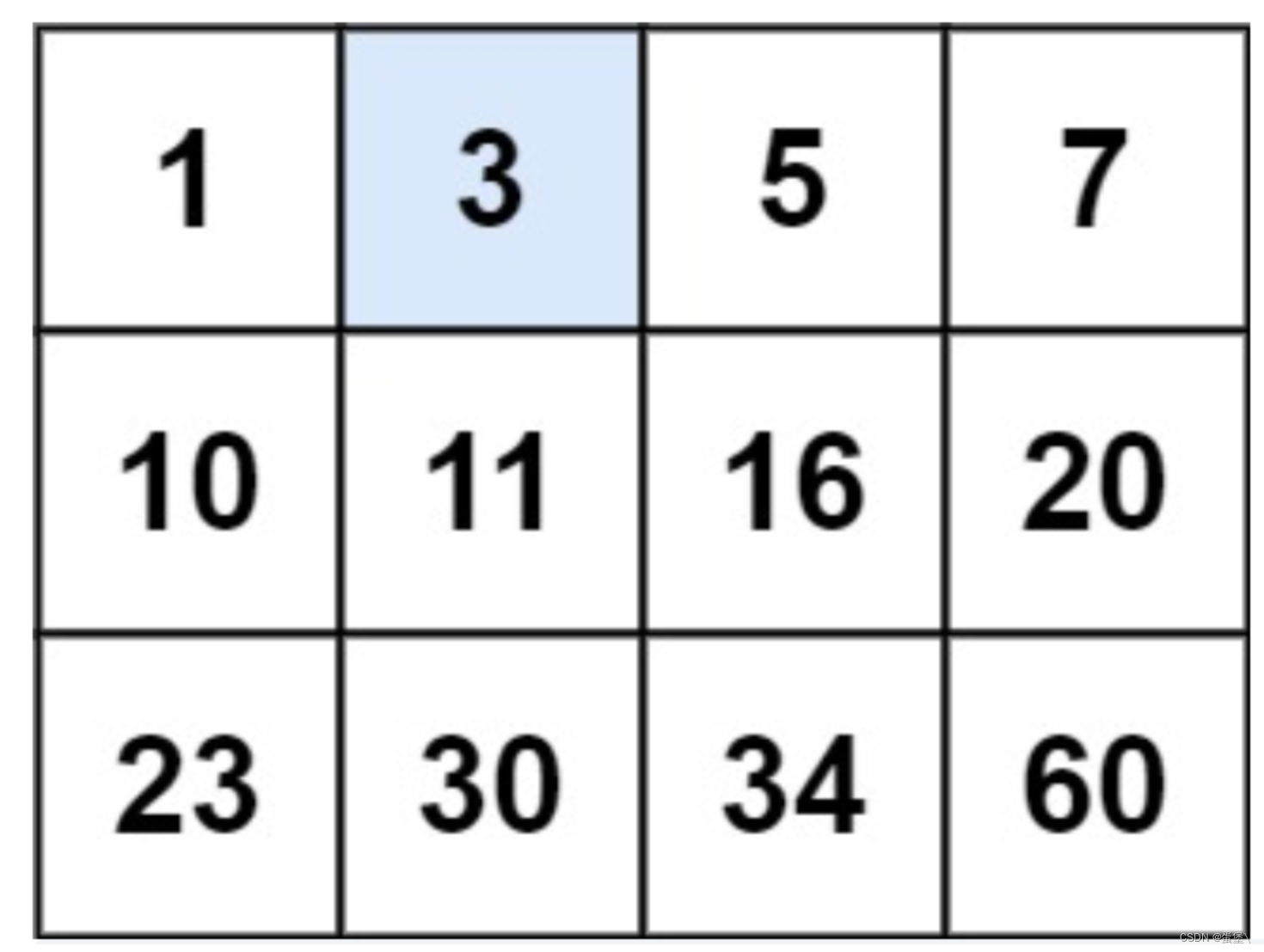
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true 

解题思路：

方法一：暴力法

1.因为每一行的元素和每一列的元素都是递增的，且当前行的末尾元素小于下一行的起始元素，所以我们从右上角开始找
2.当前元素<target，往下找
3.当前元素>target，往左找
4.当前元素=target，返回true
5.若while循环结束并跳出，说明没找到，则返回false 

源代码如下：

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m=matrix.size();
        int n=matrix[0].size();
        int i=0,j=n-1;//从右上角元素开始找
        while(i<m&&j>=0)
        {
            if(matrix[i][j]<target)
            {
                i++;
            }
            else if(matrix[i][j]>target)
            {
                j--;
            }
            else
            {
                return true;
            }
        }
        return false;
    }
}；

方法二：二分查找法

1.将矩阵看作是一组升序排序的数组
2.通过二分查找，找到目标值
3.将矩阵的下标转换为数组下标即可

源代码如下：

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m=matrix.size();
        int n=matrix[0].size(); 
        int left=0;//左边界为0
        int right=m*n-1;//右边界的下标为元素总个数-1
        while(left<=right)
        {
            int mid=(right+left)/2;
            int x=matrix[mid/n][mid%n];//将数组下标和矩阵的下标进行转换
            if(x<target)
            {
                left=mid+1;
            }
            else if(x>target)
            {
                right=mid-1;
            }
            else
            {
                return true;
            }
        }
        return false;
    }
};