🏠个人主页：fo安方的博客✨
💂个人简历：大家好，我是fo安方，考取过HCIE Cloud Computing、CCIE Security、CISP、RHCE、CCNP RS、PEST 3等证书。🐳
💕兴趣爱好：b站天天刷，题目常常看，运动偶尔做。🎐
💅欢迎大家：这里是CSDN，是我记录我的日常学习，偶尔生活的地方，喜欢的话请一键三连，有问题请评论区讨论。🌺
🥣专栏：目前专栏免费free，欢迎订阅管理类联考不迷路！这是专栏的导航页→入栏需看——全国硕士研究生入学统一考试管理类专业学位联考，阅读无烦恼。🌊
🪁 希望本文能够给读者带来一定的帮助~🌸文章粗浅，敬请批评指正！🐥

代数

整式及其运算

1.完全平方公式：$(a+b{)}^2=a^2+2ab+b^2$

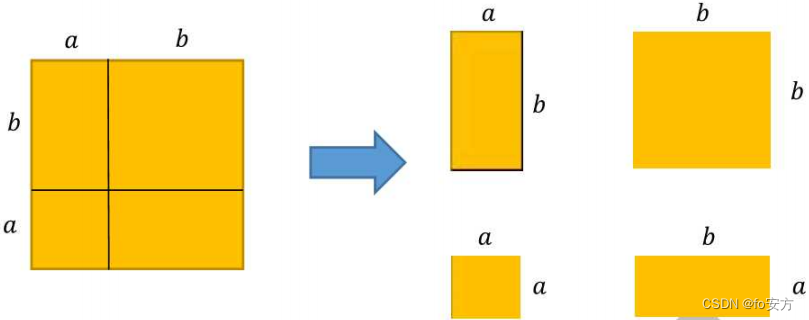
先画出一个边长为$a+b$的正方形，它的面积就是$(a+b{)}^2$。在相邻两边上分别取长度为a的一段，分别作对应边上的垂线。将正方形用两条垂直的直线进行如图切割，一个大正方形就被分成了四部分。
分别是一个边长为α的正方形、一个边长为b的正方形、两个长为b，宽为α的矩形.他们的面积分别为$a^2、b^2、a\ast b$。
大正方形被拆分成了4部分，面积也就等于四部分的面积之和$=a^2+b^2+ab+ab$，即$(a+b{)}^2=a^2+2ab+b^2$

2.$(a-b{)}^2=a^2-2ab+b^2$

这个公式有两种记忆的方法
第一种方法：对比法
可以与$(a+b{)}^2=a^2+2ab+b^2$做一个对比，不同的部分在于一个是a+b，另一个是a一b。换一个角度想，我们可以把a-b想成a+(-b)。也就是$(a-b{)}^2=[a+(-b){]}^2$。用一b替换原来公式中 b。即$(a-b{)}^2=[a+(-b){]}^2=a^2+2a\ast (-b)+(-b{)}^2=a^2-2ab+b^2$。
第二种方法：几何法

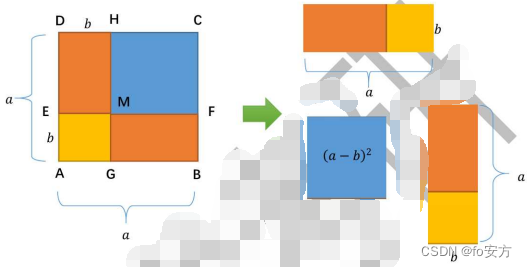
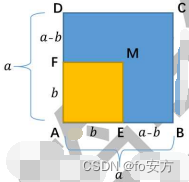
仍然是先画出一个正方形ABCD，他的边长为α、从正方形一个顶点C，在大正方形内再做一个边长为$a-b（b＜a）$的小正方形CFMH（蓝色部分)，小正方形 CFMH的面积即为所求。
延长小正方形的边长FM、HM交大正方形的边AB、AD于G、E点，将大正方形变成了三部分，$CFMH的面积=正方形ABCD的面积-其他部分面积$，其他部分被分成了两个长宽为a和b的矩形(矩形AGHD和矩形ABFE)，但是两个长方形中有一个边长为b的正方形部分(正方形AGME)是重复的.所以
$其他部分的面积=两个矩形的面积之和2a\ast b-正方形CFMH的面积b^2=2ab-b^2$也就是$蓝色正方形的面积=大正方形面积-其他部分面积$
即$(a-b{)}^2=a^2-(2ab-b^2)=a^2-2ab+b^2$

3.$a^2-b^2=(a+b)(a-b)$
平方差公式是一个很简单的公式，也是一个很常用的公式，如何巧妙地记住它，下面给出两种方法。
第一种方法是代数法，我们给等式的左边加上一个a·b，为了使原来式子的大小不变，还要再减去一个a·b，于是将a2一b2整理成$a^2-b^2+ab-ab$
再分配一下得到$(a^2+ab)-(b^2+ab)=a-(a+b)-b-(a+b)=(a+b)\cdot (a-b)$即$a^2-b^2=(a+b)\cdot (a-b)$.

第二种方法还是用几何法:
先画出一个边长为α的正方形ABCD

以A为一个顶点,以AB、AD为临边做一个边长为b的小正方形AEMF。
其中大正方形面积为$a^2$，小正方形面积为$b^2$，蓝色部分的面积即为所求$a^2-b^2$。

此时延长FM交BC于N，将矩形BNME经过平移，旋转至图中 CNB’E’位置蓝色部分就变成了一个新的矩形DFE’B’，其面积=(a+b)·(a- b).
即$a^2-b^2=(a+b)\cdot (a-b)$

数列

等差

等差数列前n项和公式：$S_n=\frac{n(a_1+a_n)}{2}$
等差数列的前n项和是考试中的重点部分，基本每年都会进行考察。
通常记这个式子有一个口诀叫“首项加末项乘以项数除以2"，那么这句口诀又是怎么来的呢？首先，将前n项和的表达式写出来：
$S_n=a_1+a_2+a_3+\dots +a_{n-1}+a_n$
再将前n项和的表达式列一遍，只不过这次，用脚标倒序的顺序表示：
$S=a_n+a_{n-1}+a_{n-2}+\dots +a_2+a_1$
将两个式子等号左右两边分别相加
等号左边=2$S_n$；
等号右边首尾分别相加

根据等差数列的脚标性质，每一个红框内的值都等于$a_1+a_n$，一共有n 组，所以等号右边$=n\cdot (a_1+a_n)$
得到$2S_n=n\ast (a_1+a_n)$，即$S_n=\frac{n(a_1+a_n)}{2}$
另一种方法，因为等差数列相邻两项之差都是公差，我们可以将前n项排列成一个等腰梯形，第一层是a，第二层是$a_2=a_1+d$，第三层是$a_3=a_1+2d......$以此类推，第n层是$a_n$。前n项和$S_n$可以看做是这个等腰梯形的面积，上底为$a_1$，下底为$a_n$。高为n (一共n项) 。所以$S_n=\frac{1}{2}(上底＋下底)\cdot 高=\frac{n(a_1+a_n)}{2}$。

等比

等比数列前n项和公式$S_n=\frac{a_1(1-q^n)}{1-q}=\frac{a_1-a_{n}q)}{1-q}（q\ne 1）$
等比数列前n项和是数列的考察中另一个最常用的公式。下面介绍如何巧记这个公式.首先我们先写出前n项和的表达式，仍然是$S_n=a_1+a_2+a_3+\dots 十a_{n-1}+a_n$。
我们将一个$S_n$去掉首项，得到$S_n-a_1=a_2+a_3+a_4+\dots +a_{n-1}+a_n$.
将另一个$S_n$去掉最后一项，得到$S_n-a_n=a_1+a_2+a_3+\dots +an-2+a_{n-1}$。这时我们可以如图所示进行观察：

上边式子等号右面的每一项都是下边等式右边的每一项的q倍。
也就是$\frac{S_n-a_1}{S_n-a_n}=\frac{a_2+a_3+a_4+...+a_{n-1}+a_n}{a_1+a_2+a_3+...+a_{n-2}+a_{n-1}}=\frac{a_1+a_2+a_3+...+a_{n-2}+a_{n-1}}{a_1+a_2+a_3+...+a_{n-2}+a_{n-1}}$
得到$\frac{S_n-a_1}{S_n-a_n}=q$
整理可得$S_n-a_1=q\ast (S_n-a_n)$
$(1-q)\ast S_n=a_1-a_{n}q$
即$S_n=\frac{a_1-a_{n}q}{1-q}$

数列中$S_n,S_{2n}-S_n,S_{3n}-S2n\dots$的讨论

首先将三个式子的表达式列写出来：
$S_n=a_1+a_2+a_3+\dots ＋a_{n-1}+a_n$
$S_{2n}-S_n=a_{n+1}+a_{n+2}+a_{n+3}+\dots +a_{2n-1}+a_{2n}$
$S_{3n}-S_{2n}=(a_{2n+1}+a_{n+2}+a_{n+3}+\dots +a_{3n-1}+a_{3n}$
先将Sn与S2n的每一项对比来看：

对应的每一项脚标之差都是n。
当原数列{a,}是等差数列时
此时有an+1= a1+ nd; an+2= az+ nd;…;azn = an+ndS2n - Sn= (a1+ nd)+(az+ nd)+…+(an-1+ nd) +(an +nd)
= a1+ az+ a3+…+an-1+ an + n : nd =Sn+ n2·d
同理验证S3n - Szn与S2n一S,可得: s3n -s2n= s2n -Sn+n2·d进而得出Sn,S2n -Sn. S3n- S2n…仍为等差数列，公差为n·d.当原数列{an}是等比数列时
此时有an+1 = a1·q”; an+2 = az q;…; azn= an 9"S2n-Sn = a1·q"+ az·q”+…+anL1-q”+an·q"
= (a1+ a2+…+ an-1+a)·q"=Sn ·q"”
同理验证S3n -Szn与S2n-Sn可得:S3n-Szn=(Szn - s)·q".进而可以得出Sn, Szn -Sn，53n- Sz4……仍为等比数列，公比为q"".
综上，我们可以得出结论: