【半监督图像分类 ICLR 2023】FreeMatch

论文题目：FREEMATCH: SELF-ADAPTIVE THRESHOLDING FOR SEMI-SUPERVISED LEARNING

中文题目：Freematch：用于半监督学习的自适应阈值

论文链接：https://arxiv.org/abs/2205.07246

论文代码：

论文团队：

发表时间：

DOI:

引用：

引用数：

摘要

半监督学习(SSL)由于基于伪标记和一致性正则化的各种方法所带来的优异性能而取得了巨大的成功。

然而，我们认为，现有的方法要么采用预先定义/固定的门限，要么采用自适应门限调整方案，可能无法更有效地利用未标记数据，从而导致性能低下和收敛速度慢。

我们首先分析了一个激励示例，以获得关于期望阈值与模型学习状态之间关系的直观性。

在此基础上，我们提出了FreeMatch模型，根据模型的学习状态自适应地调整置信度阈值。 我们进一步引入了一个自适应的类公平性正则化惩罚，以鼓励模型在早期训练阶段进行多样化的预测。

大量的实验表明，Freematch的优越性，特别是在标记数据极其稀少的情况下。 Freematch在CIFAR-10（每类1个标签）、STL-10（每类4个标签）和ImageNet（每类100个标签）上分别实现了5.78%、13.59%和1.28%的错误率降低。 此外，Freematch还可以提高不平衡SSL的性能。

1. 介绍

深度学习的优越性能严重依赖于有足够标记数据的监督训练。 然而，获取大量标签数据仍然费力且昂贵。 为了减轻这种依赖，半监督学习(SSL)被开发出来，通过利用大量未标记数据来提高模型的泛化性能。 伪标记和一致性正则化是为现代SSL设计的两种流行范式。 最近，他们的组合显示出了有希望的结果。 该模型的核心思想是遵循SSL中的平滑性和低密度假设，对相同的未标记数据在不同的扰动下产生相似的预测或相同的伪标记。

这些基于阈值的方法的一个潜在的局限性是，它们要么需要一个固定的阈值，要么需要一个特殊的阈值调整方案来计算仅使用可信未标记样本的损失。 具体来说，uda和fixmatch保留固定的高阈值以确保伪标签的质量。 然而，一个固定的高阈值（0.95）会导致早期训练阶段的数据利用率低，并忽略了不同班级的不同学习困难。 Dash和Adamatch提出，随着训练的进展，逐渐增长固定的全局（特定于数据集的）阈值。 虽然提高了无标记数据的利用率，但它们的自组织阈值调整方案是由超参数任意控制的，从而与模型的学习过程脱节。 FlexMatch论证了不同的类应该有不同的局部（特定于类的）阈值。 虽然局部阈值考虑了不同类别的学习困难，但它们仍然是从预定义的固定全局阈值映射而来的。 ADSH(Guo&Li，2022)通过优化每个类的伪标签数量，从预定义的阈值中获得自适应阈值，用于非平衡半监督学习。 简而言之，这些方法在根据模型的学习进度调整阈值方面可能是不能够或不足的，从而阻碍了训练过程，尤其是当标记数据太少而无法提供足够的监督时。

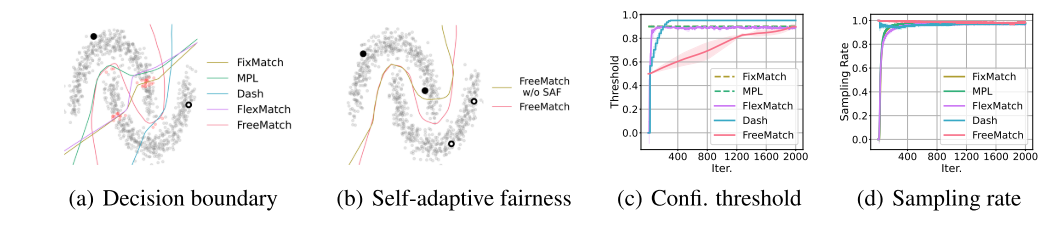
图1：演示Freematch如何在“双月”数据集上工作。 (A)Freematch和其他SSL方法的决策边界。 (b)自适应公平性(SAF)在每类两个标记样本上的判决边界改进。 ©类平均置信度阈值。 (d)训练期间Freematch的ClassAverage抽样率。 实验细节见附录A。

例如，如图1(a)所示，在每个类只有1个标记样本的“双月”数据集上，通过以前的方法获得的决策边界在低密度假设中是失败的。 那么，自然就产生了两个问题：1）是否有必要基于模型学习状态来确定阈值？ （2）如何自适应调整阈值以获得最佳训练效率

在本文中，我们首先利用一个激励的例子来证明不同的数据集和类应该根据模型的学习状态来确定它们的全局（特定于数据集）和局部（特定于类）阈值。 直观上，我们需要一个较低的全局阈值来利用更多的未标记数据，并在早期训练阶段加快收敛速度。 随着预测置信度的增加，需要更高的全局阈值来过滤掉错误的伪标签以缓解确认偏差（Arazo et al.，2020)。 此外，应该根据模型对其预测的置信度在每个类上定义一个局部阈值。 图1(a)中的“双月”示例表明，当根据模型的学习状态调整阈值时，决策边界更加合理。

然后，我们提出Freematch根据每个班级的学习状况以自适应的方式调整阈值（Guo et al.，2017)。 特别地，Freematch使用自适应阈值(SAT)技术通过未标记数据置信度的指数移动平均(EMA)来估计全局（特定于数据集）和局部（特定于类）阈值。 为了更有效地处理几乎没有监督的设置（Sohn et al.，2020)，我们进一步提出了一个类公平目标，以鼓励模型在所有类之间产生公平（即多样化）的预测（如图1(b))。 Freematch的总体训练目标是最大化模型输入和输出之间的互信息（John Bridle，1991)，在未标记数据上产生自信和多样的预测。 基准结果验证了其有效性。 最后，我们的贡献是：

• 通过一个激励例子，讨论了阈值为什么要反映模型的学习状态，并为阈值调整方案的设计提供了一些直观的依据。
• 提出了一种新的自适应门限化(SAT)和自适应类公平性正则化(SAF)算法FREEMATCH。 SAT是一种无需手动设置阈值的阈值调整方案，而SAF鼓励不同的预测。
• 大量的结果表明，Freematch在各种SSL基准上具有优越的性能，尤其是在标签数量非常有限的情况下（例如，在CIFAR-10上，每类1个标签样本的错误减少了5.78%）。

2. 样例

在这一节中，我们介绍了一个二元分类的例子来激励我们的阈值调整方案。 尽管简化了实际的模型和培训过程，但该分析还是引出了一些有趣的含义，并为如何设置阈值提供了见解。

本文旨在说明SSL可信度阈值的自适应性和粒度的增加的必要性。 受(Yang&Xu，2020)的启发，我们考虑了一个二元分类问题，其中真分布是两个高斯分布的偶数混合（即标号y同样可能是正(+1)或负(-1))。 输入x具有以下条件分布：
$$X\mid Y=-1\sim \mathcal{N}({\mu }_1,{\sigma }_1^2),X\mid Y=+1\sim \mathcal{N}({\mu }_2,{\sigma }_2^2).$$
我们假定${\mu }_2>{\mu }_1$，但不损失一般性。 假设我们的分类器输出置信度得分$s(x)=1/[\dot{1+}\exp (-\beta (x-\frac{{\mu }_1+{\mu }_2}{2}))]$，其中$\beta$是反映模型学习状态的正参数，随着模型变得更加自信，它有望在训练过程中逐渐增长。 注意，$\frac{{\mu }_1+{\mu }_2}{2}$实际上是贝叶斯的最优线性决策边界。 我们考虑了一个固定阈值$\tau \in (\frac{1}{2},1)$用于生成伪标签的情形。 当$s(x)>\tau$时，样本x被赋伪标记+1，当$s(x)<1-\tau .$时，被赋伪标记-1。 如果$1-\tau \le s(x)\le \tau$，则伪标号为0（屏蔽）。

然后我们推导出如下定理来说明自适应阈值的必要性：定理2.1。

2.1 定理

对于如上所述的二元分类问题，伪标号$Y_p$具有以下概率分布：
$$\begin{array}{rl}P(Y_p=1)& =\frac{1}{2}\Phi (\frac{\frac{{\mu }_2-{\mu }_1}{2}-\frac{1}{\beta }\log (\frac{\tau }{1-\tau })}{{\sigma }_2})+\frac{1}{2}\Phi (\frac{\frac{{\mu }_1-{\mu }_2}{2}-\frac{1}{\beta }\log (\frac{\tau }{1-\tau })}{{\sigma }_1})\\ P(Y_p=-1)& =\frac{1}{2}\Phi (\frac{\frac{{\mu }_2-{\mu }_1}{2}-\frac{1}{\beta }\log (\frac{\tau }{1-\tau })}{{\sigma }_1})+\frac{1}{2}\Phi (\frac{\frac{{\mu }_1-{\mu }_2}{2}-\frac{1}{\beta }\log (\frac{\tau }{1-\tau })}{{\sigma }_2}),\\ P(Y_p=0)& =1-P(Y_p=1)-P(Y_p=-1),\end{array}$$
其中$\Phi$是标准正态分布的累积分布函数。 此外，$P(Y_p=0)$随着${\mu }_2-{\mu }_1$的减小而增大。

证明在附录B中提供。定理2.1有以下含义或解释：

1. 通常，未标记数据利用率（采样率）$1-P(Y_p=0)$由阈值$\tau$直接控制。 随着置信度阈值τ的增大，未标记数据的利用率降低。 在早期训练阶段，由于β仍然很小，采用高阈值可能会导致采样率低和收敛速度慢。
2. 更有趣的是，如果${\sigma }_1\ne {\sigma }_2$，则$P(Y_p=1)\ne P(Y_p=-1)$。 实际上，$\tau$越大，伪标签越不平衡。 这可能是不可取的，因为我们的目标是解决一个平衡的分类问题。 不平衡的伪标签可能会扭曲决策边界，导致所谓的伪标签偏差。 一个简单的解决方法是使用特定于类的阈值τ2和1-τ1来分配伪标签。
3. 采样速率$1-P(Y_p=0)$随着${\mu }_2-{\mu }_1$的减小而减小。 换句话说，这两个类越相似，一个未标记的样本就越有可能被掩盖。 当两类相似度越高，特征空间中的混合样本越多，模型对其预测的可信度就越低，因此需要一个适度的阈值来平衡采样率。 否则，我们可能没有足够的样本来训练模型来分类已经很难分类的类。

定理2.1提供的直觉是，在早期训练阶段，$\tau$应该较低，以鼓励不同的伪标签，提高未标记数据的利用率和加快收敛速度。 然而，随着训练的继续和$\beta$变大，持续的低阈值会导致不可接受的确认偏差。 理想情况下，阈值$\tau$应随$\beta$一起增加，以始终保持稳定的采样率。 由于不同的类具有不同级别的类内多样性（不同的$\sigma$)，并且一些类比其他类更难分类($\mu 2-\mu 1$较小），因此需要一个细粒度的类特定阈值来鼓励将伪标签公平地分配给不同的类。 面临的挑战是如何设计一个综合考虑各种影响的阈值调整方案，这也是本文的主要贡献。 我们通过绘制训练期间的平均阈值趋势和边缘伪标签概率（即采样率）来演示我们的算法，如图1©和1(d)所示。 总而言之，我们应该通过模型的预测来估计学习状态，从而确定全局（特定于数据集）和局部（特定于类）阈值。 然后，我们详细介绍了Freematch。

3. 准备工作

在SSL中，训练数据由标记数据和未标记数据组成。 设${\mathcal{D}}_L=\{(x_b,y_b):b\in [N_L]\}$和 D U = { u b : b ∈ [ N U ] } \mathcal{D}_U= \{u_{b}:b\in[N_{U}]\} DU​={ub​:b∈[NU​]}为标记数据和未标记数据，其中NL和NU分别为它们的样本数。 标记数据的监督损失为：
$${\mathcal{L}}_s=\frac{1}{B}\sum _{b=1}^B\mathcal{H}(y_b,p_m(y|\omega (x_b))),$$
其中$B$是批量大小，$\mathcal{H}(\cdot ,\cdot )$是交叉熵损失，$\omega (\cdot )$是随机数据增广函数，pm(·)是模型的输出概率。

对于未标记的数据，我们重点研究了基于交叉熵损失的伪标记，并给出了熵最小化的置信度阈值。 我们还采用UDA（Xie et al.，2020a)介绍的“弱强增强”策略。 形式上，针对未标记数据的无监督训练目标是：
$${\mathcal{L}}_u=\frac{1}{\mu B}\sum _{b=1}^{\mu B}1(\max (q_b)>\tau )\cdot \mathcal{H}({\hat{q}}_b,Q_b).$$
我们用$q_b$和$Q_b$分别表示$p_m(y|\omega (u_b))$和$p_m(y|\Omega (u_b))$的缩写。 $\widehat{q_b}$是由$q_b$转换而来的硬“一热”标签，μ是未标记数据批量大小与标记数据批量大小的比值，$1(\cdot >\tau )$是基于置信度阈值化的指示函数，$\tau$是阈值。 弱增强（即随机裁剪和翻转）和强增强（即Randaugment Cubuk et al.(2020))分别用ω(·)和$\Omega (\cdot )$表示。

此外，通常引入一个公平目标${\mathcal{L}}_f$，鼓励模型以相同的频率预测每一类，其形式通常为${\mathcal{L}}_f=\mathbf{U}\log {\mathbb{E}}_{\mu B}\left[q_b\right]$，其中$\mathbf{U}$是一个均匀的先验分布。人们可能会注意到，使用统一先验不仅防止了对非统一数据分布的泛化，而且还忽略了一个事实，即由于采样机制，小批量的底层伪标签分布可能是不平衡的。整批的一致性对于每个类阈值样本的合理利用至关重要，特别是对于早期训练阶段。

4. FreeMatch

我们提出的FreeMatch包含两部分：自适应阈值 和 自适应公平正则化惩罚。下面分别进行介绍。

4.1 自适应阈值

我们主张，确定SSL的阈值的关键是，阈值应反映学习状态。学习效果可以通过一个经过良好校准的模型的预测置信度来估计（Guo等人，2017）。因此，我们提出了自适应阈值（SAT），通过利用训练期间的模型预测，自动定义和自适应调整每个类别的信心阈值。SAT首先估计了一个全局阈值，作为来自模型的置信度的EMA。然后，SAT通过本地特定类别的阈值来调节全局阈值，该阈值被估计为来自模型的每个类别的概率的EMA。当训练开始时，阈值很低，以接受更多可能正确的样本进入训练。随着模型变得更加自信，阈值会自适应地增加，以过滤掉可能不正确的样本，减少确认偏差。因此，如图2所示，我们将SAT定义为${\tau }_t(c)$，表示第t次迭代时c类的阈值。

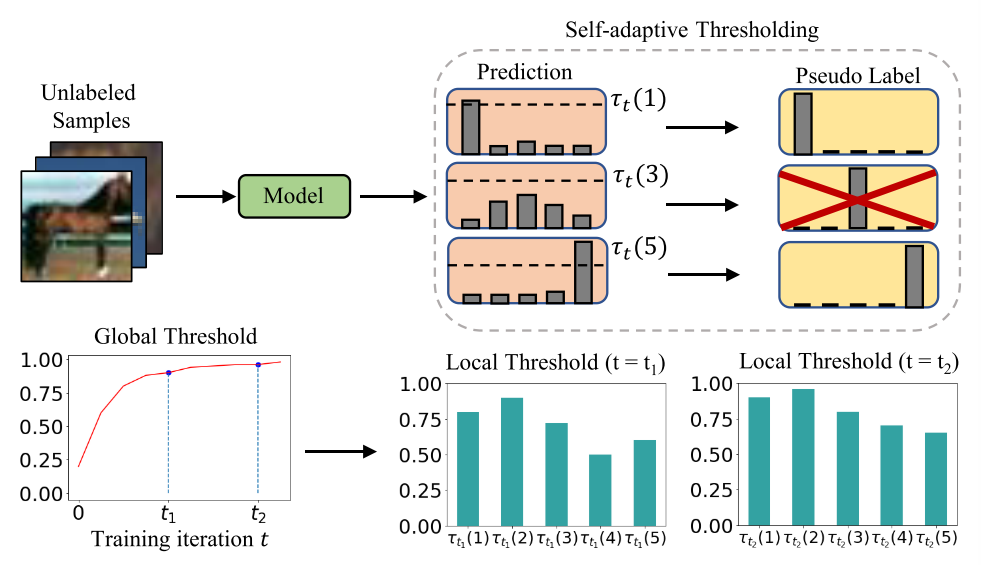
图2：自适应阈值(SAT)的说明。 Freematch采用全局和局部自适应阈值，由未标记样本的预测统计量的均方差计算。 过滤后的（掩蔽）样品用红色X标记。

自适应的全局阈值

我们根据以下两个原则设计全局阈值。首先，SAT中的全局阈值应该与模型对未标记数据的信心有关，反映出整体的学习状况。此外，全局阈值应该在训练过程中稳定地增加，以确保错误的伪标签被丢弃。我们将全局阈值${\tau }_t$设置为模型对未标注数据的平均信心，其中$t$代表第$t$个时间步长（迭代）。然而，由于数据量大，在每个时间步长甚至每个训练纪元计算所有未标记数据的置信度是非常耗时的。相反，我们将全局置信度估计为每个训练时间步骤的置信度的指数移动平均值（EMA）。我们将${\tau }_t$初始化为$\frac{1}{C}$，其中C表示类的数量。全局阈值τt被定义并调整为：
$${\tau }_t=\{\begin{array}{ll}\frac{1}{C},& \text{if}t=0,\\ \lambda {\tau }_{t-1}+(1-\lambda )\frac{1}{\mu B}{\sum }_{b=1}^{\mu B}\max (q_b),& \text{otherwise,}\end{array}$$
自适应局部阈值局部阈值的目的是以特定于类的方式调制全局阈值，以考虑类内多样性和可能的类邻接性。 我们计算模型对每个类别$C$的预测的期望，以估计特定类别的学习状态：
$${\tilde{p}}_t(c)=\{\begin{array}{ll}\frac{1}{C},& \text{if}t=0,\\ \lambda {\tilde{p}}_{t-1}(c)+(1-\lambda )\frac{1}{\mu B}{\sum }_{b=1}^{\mu B}{q}_b(c),& \text{otherwise,}\end{array}$$
其中${\tilde{p}}_t=[{\tilde{p}}_t(1),{\tilde{p}}_t(2),\dots ,{\tilde{p}}_t(C)]$是包含所有${\tilde{p}}_t(c)$的列表。 综合全局阈值和局部阈值，我们得到最终的自适应阈值${\tau }_t(c)$
τ t ( c ) = MaxNorm ⁡ ( p ~ t ( c ) ) ⋅ τ t = p ~ t ( c ) max ⁡ { p ~ t ( c ) : c ∈ [ C ] } ⋅ τ t , \tau_t(c)=\operatorname{MaxNorm}(\tilde p_t(c))\cdot\tau_t=\frac{\tilde p_t(c)}{\max\{\tilde p_t(c):c\in[C]\}}\cdot\tau_t, τt​(c)=MaxNorm(p~​t​(c))⋅τt​=max{p~​t​(c):c∈[C]}p~​t​(c)​⋅τt​,
其中$\text{MaxNorm}$是最大归一化（即$x^{\prime }=\frac{x}{\max (x)}$)。 最后，第t次迭代时的无监督训练目标Lu为：
$${\mathcal{L}}_u=\frac{1}{\mu B}\sum _{b=1}^{\mu B}1(\max (q_b)>{\tau }_t(\arg \max (q_b))\cdot \mathcal{H}({\hat{q}}_b,Q_b).$$

4.2 自适应公平

我们将第3节中提到的类公平性目标包含到Freematch中，以鼓励模型对每个类做出不同的预测，从而产生有意义的自适应阈值，特别是在标记数据很少的情况下。 我们不像在（Arazo et al.，2020)中那样使用统一的先验，而是使用来自EQ的模型预测的EMA～PT。 6作为对未标记数据上预测分布的期望的估计。 我们优化了Mini-Batch上$\widehat{p_t}$和$\overline{p}={\mathbb{E}}_{\mu B}[p_m(y|\Omega (u_b))]$的交叉熵作为$H({\mathbb{E}}_u[p_m(y|u)])$的估计值。 考虑到潜在的伪标签分布可能不是均匀的，我们提出用自适应的方式调整公平目标，即通过伪标签的直方图分布来规格化概率期望，以对抗不平衡的负面影响，如：
$$\begin{array}{r}\overline{p}=\frac{1}{\mu B}\sum _{b=1}^{\mu B}1\left(\max \left(q_b\right)\ge {\tau }_t(\arg \max \left(q_b\right)\right)Q_b,\\ \overline{h}={\mathrm{Hist}}_{\mu B}\left(1\left(\max \left(q_b\right)\ge {\tau }_t(\arg \max \left(q_b\right)\right){\hat{Q}}_b\right).\end{array}$$
与 "pt "类似，我们计算 "ht "为：
$${\tilde{h}}_t=\lambda {\tilde{h}}_{t-1}+(1-\lambda ){\mathrm{Hist}}_{\mu B}\left({\hat{q}}_b\right).$$
第t次迭代时的自适应公平(SAF)LF表述为：
$${\mathcal{L}}_f=-\mathcal{H}\left(\mathrm{SumNorm}\left(\frac{{\tilde{p}}_t}{{\tilde{h}}_t}\right),\mathrm{SumNorm}\left(\frac{\bar{p}}{\bar{h}}\right)\right),$$
其中Sumnorm=(·)/(·)。 SAF通过直方图分布归一化后，使每个小批量的输出概率期望接近于模型的一个边际类分布。 它帮助模型产生不同的预测，特别是在几乎没有监督的环境下（Sohn et al.，2020)，从而收敛得更快，泛化得更好。 这也显示在图1(b)中。

Freematch第t次迭代的总体目标是：
$$\mathcal{L}={\mathcal{L}}_s+w_u{\mathcal{L}}_u+w_f{\mathcal{L}}_f,$$

其中$w_u$和$w_f$分别代表${\mathcal{L}}_u$和${\mathcal{L}}_f$的损失权重。有了${\mathcal{L}}_u$和${\mathcal{L}}_f$，FreeMatch就能使其输出和输入之间的相互信息最大化。我们在附录的算法1中介绍了FreeMatch的程序。

5. 实验

参考资料

ICLR 2023半监督学习最高分论文FreeMatch: 自适应阈值法 - 知乎 (zhihu.com)