15.三数之和

1.题目描述

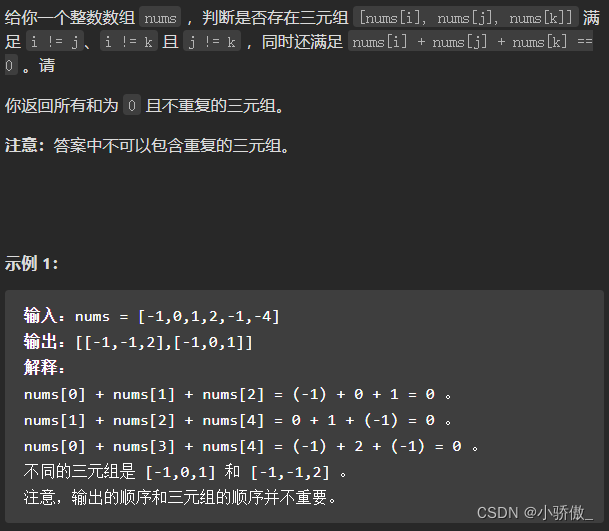
在这里插入图片描述

详情leetcode链接

2.双指针法

2.1思路及注意点

将数组排序，有一层for循环，i从下标0开始，同时定义一个下标left在i+1的位置上，定义下标right在数组末尾位置。
依次在数组中找到abc，使得a + b +c =0，这里相当于 a =nums[i]，b = nums[left]，c = nums[right]。
若nums[i] + nums[left] + nums[right] > 0 就说明此时三数之和大了，因为数组是排序后了，所以right下标就应该向左移动，这样才能让三数之和小一些。
若nums[i] + nums[left] + nums[right] < 0 说明此时三数之和小了，left向右移动，才能让三数之和大一些，直到left与right相遇为止。

去重注意：
因为本题要求不能重复的三元组，所以需要对每个数进行去重。

最外层for循环对a去重时，错误写法：if条件为nums[i]=nums[i+1],这样判断的是结果集中是否有重复元素，会误跳过结果集
正确写法：if条件为nums[i]=nums[i-1]，举例{-1，-1，2}

b和c去重时，应该在找到一个三元组后进行去重

2.2代码实现

/**
 * 双指针法：(推荐)
 * 思路：
 *   将数组排序，有一层for循环，i从下标0开始，同时定义一个下标left在i+1的位置上，定
 * 义下标right在数组末尾位置，依次在数组中找到abc，使得a + b +c =0，这里相当于 a =
 * nums[i]，b = nums[left]，c = nums[right]。
 *   若nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了，因为数组是
 * 排序后了，所以right下标就应该向左移动，这样才能让三数之和小一些。
 *   若nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了，left向右移
 *动，才能让三数之和大一些，直到left与right相遇为止。
 *    
 * 时间复杂度：O(n^2)
 * 空间复杂度：O(1) 
 *  */
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(nums);//对结果集进行排序
        for (int i = 0; i < nums.length; i++) {
            //因为对结果集进行了排序，若第一个大于0，则必然不会组成规定的三元组
            if (nums[i]>0){
                return result;
            }
            // 错误去重a方法，将会漏掉-1,-1,2 这种情况
            /*
            if (nums[i] == nums[i + 1]) {
                continue;
            }
            */
            //正确去重方法
            if (i > 0 && nums[i] == nums[i-1]){
                continue;
            }
            int left = i+1;
            int right = nums.length - 1;
            //边界条件考虑：若left = right，b和c相当于同一个数，不符合题意
            while (right > left){
                int sum = nums[i] + nums[left] + nums[right];
                if (sum > 0){
                    right --;
                }else if (sum < 0) {
                    left ++;
                }else {
                    result.add(Arrays.asList(nums[i],nums[left],nums[right]));
                    //当找到一个三元组后，对b和c去重
                    while (right > left && nums[left]==nums[left+1]) left++;
                    while (right > left && nums[right]==nums[right-1]) right--;
                    left ++;
                    right --;
                }
            }
        }
        return result;
    }
}

3.哈希法(有待修正)

3.1 思路

两层for循环就可以确定 a 和b 的数值了，然后使用哈希法来确定 0-(a+b) 是否在数组里出现过
因为结果数组中不包含重复的三元组，所以需要依次对三个数进行去重及对结果去重

3.2 代码实现

/**
 * 暴力法：双层for循环(不推荐)
 * 思路：两层for循环就可以确定 a 和b 的数值了，
 *       然后使用哈希法来确定 0-(a+b) 是否在 数组里出现过，
 *       因为结果数组中不包含重复的三元组，所以需要依次对三个数进行去重及对结果去重
 *       此法代码编写时间复杂度高且需要去重考虑的细节很多，复杂不推荐
 * 时间复杂度：O(n^2)
 * 空间复杂度：O(n) //额外的set开销
 *
 */
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(nums);
        Set<Integer> set = new HashSet<>();
        Set<Integer> filter = new HashSet<>();
        for (int i = 0; i < nums.length; i++){
            if (nums[i] > 0){//若数组的第一个数大于0，直接返回
                return result;
            }
            if (i > 0 && nums[i]==nums[i-1]){//对第一个数去重
                continue;
            }
            for (int j = i + 1; j < nums.length; j++){
                if (j > i+1 && nums[j]==nums[j-1]){//对第二个数去重
                    continue;
                }
                int third = 0 - (nums[i] + nums[j]);
                if (set.contains(third) && !filter.contains(nums[j])){
                    List<Integer> singResult = new ArrayList<>();
                    singResult.add(nums[i]);
                    singResult.add(nums[j]);
                    singResult.add(third);
                    result.add(singResult);
                    set.remove(third);//对第三个数去重
                    filter.add(third);//防止有重复的集合
                }else {
                    set.add(nums[j]);
                }
            }
        }
        return result;
    }
}