198. 打家劫舍

 1. 确定dp数组（dp table）以及下标的含义

         dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]

2. 确定递推公式

dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

3. dp数组如何初始化

        递推公式的基础就是dp[0] 和 dp[1]。 从dp[i]的定义上来讲，dp[0] 一定是 nums[0]，dp[1]就是nums[0]和nums[1]的最大值即：dp[1] = max(nums[0], nums[1]);

4. 确定遍历顺序

        dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的，那么一定是从前到后遍历

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n];

        if(n == 1){
            return nums[0];
        }

        dp[0] = nums[0];
        dp[1] = Math.max(nums[0], nums[1]);

        for(int i = 2; i < n; i++){
            dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i]);
        }

        return dp[n-1];
    }
}

 213. 打家劫舍 II       

这题想法很巧妙 有点像 分而治之？

情况1 考虑包含首元素，不包含尾元素

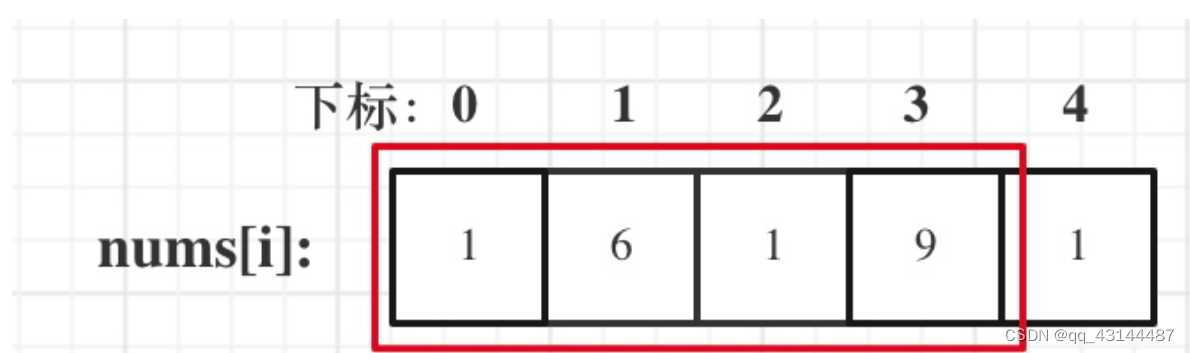
 情况2 考虑包含尾元素，不包含首元素

 然后两种情况分布进行打家劫舍 取最大值即可

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        if(n == 1){
            return nums[0];
        }
        int rob1 = robAction(nums, 0, n-2);
        int rob2 = robAction(nums, 1, n-1);
        return Math.max(rob1, rob2);
    }

    private int robAction(int[] nums, int start, int end){
        int n = nums.length;
        int[] dp = new int[n];
        if(start == end){
            return nums[start];
        }
        
        dp[start] = nums[start];
        dp[start + 1] = Math.max(nums[start], nums[start + 1]);

        for(int i = start + 2; i <= end; i++){
            dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i]);
        }

        return dp[end];
    }
}

337. 打家劫舍 III

好难 想不到

dp数组（dp table）以及下标的含义：下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱。

class Solution {
    public int rob(TreeNode root) {
        int[] res = postOrder(root);
        return Math.max(res[0], res[1]);
    }

    private int[] postOrder(TreeNode root){
        if(root == null){
            return new int[]{0, 0};
        }

        int[] left = postOrder(root.left);
        int[] right = postOrder(root.right);

        int[] status = new int[2];
        status[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        status[1] = root.val + left[0] + right[0];

        return status;
    }
}