分析：

        补题。当时不明白的点是如何快速查询相同元素的下标，可以用last[a[i]]表示与a[i]相同的最近的一个数的下标，可以遍历数组的同时实现下标的查询和变化，不断通过遍历来更新last[a[i]]的值，即last[a[i]]=i。

        然后是状态转移方程，存在两种情况，第一种是找到最近的相同下标加入新的一段区间。

所以得到状态转移方程表示为dp[last[a[i]]]+i-last[i]，不是i-last[a[i]]+1是因为last[a[i]]的一个元素会被计算两次。

 

第二种是找到最近的相同下标并且成为一段新的区间再加上之前的方案数，所以状态转移方程为dp[last[a[i]]-1]+i-last[a[i]+1。

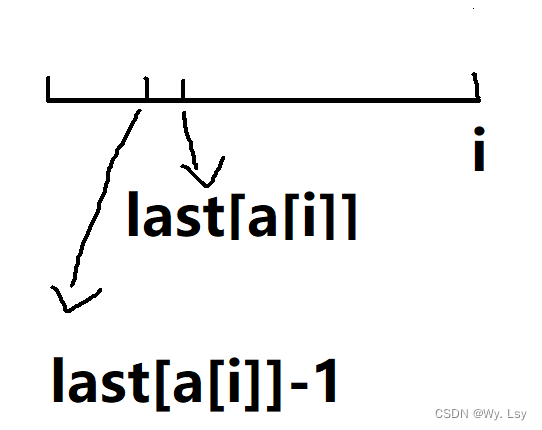
 最后状态转移方程为dp[i]=max(dp[last[a[i]]]+i-last[a[i]],dp[last[a[i]]-1]+i-last[a[i]]+1)。

代码：

#include <bits/stdc++.h>

#define x first
#define y second

using namespace std;

typedef long long ll;
typedef pair<int,int> pii;

const int N=2e5+10;

int a[N];
int f[N];
int last[N];

int main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	
	int t;
	cin>>t;
	while(t--)
	{
		int n;
		cin>>n;
		for(int i=1;i<=n;i++)
		{
			cin>>a[i];
			last[a[i]]=-1;
		}
		for(int i=1;i<=n;i++)
		{
			f[i]=f[i-1];
			if(last[a[i]]!=-1)
			{
				int res=max(f[last[a[i]]]+i-last[a[i]],f[last[a[i]]-1]+i-last[a[i]]+1);
				f[i]=max(f[i],res);
			}
			last[a[i]]=i;
		}
		cout<<f[n]<<'\n';
	}
}