第一章 绪论

第一节 什么是数据结构？

估猜以下软件的共性：学生信息管理、图书信息管理、人事档案管理。
　　数学模型：用符号、表达式组成的数学结构，其表达的内容与所研究对象的行为、特性基本一致。
信息模型：信息处理领域中的数学模型。
　　数据结构：在程序设计领域，研究操作对象及其之间的关系和操作。
忽略数据的具体含义，研究信息模型的结构特性、处理方法。
第二节 概念、术语

一、有关数据结构的概念

数据：对客观事物的符号表示。
例：生活中还有什么信息没有被数字化？
身份证，汽车牌号，电话号码，条形代码……
数据元素：数据的基本单位。相当于"记录"。
一个数据元素由若干个数据项组成，相当于"域"。
数据对象：性质相同的数据元素的集合。
数据结构：相互之间存在特定关系的数据集合。
四种结构形式：集合、线性、树形、图(网)状
形式定义：(D，S，P)
D：数据元素的集合(数据对象)
S：D上关系的有限集
P：D上的基本操作集
逻辑结构：关系S描述的是数据元素之间的逻辑关系。
　　存储结构：数据结构在计算机中的存储形式。
顺序映象、非顺序映象、索引存储、哈希存储
逻辑结构与存储结构的关系：
逻辑结构：描述、理解问题，面向问题。
存储结构：便于机器运算，面向机器。
程序设计中的基本问题：逻辑结构如何转换为存储结构？

二、有关数据类型的概念

数据类型：值的集合和定义在该值集上的一组操作的总称。
　　 包括：原子类型、结构类型。
　　抽象数据类型(ADT)：一个数学模型及该模型上的一组操作。
核心：是逻辑特性，而非具体表示、实现。
课程任务：
学习ADT、实践ADT。
如：线性表类型、栈类型、队列类型、数组类型、广义表类型、树类型、图类型、查找表类型……
实践指导：
为了代码的复用性，采用模块结构。
如：C中的头文件、C++中的类

第三节 ADT的表示与实现

本教材中，算法书写习惯的约定。
数据元素类型ElemType：int,float,char, char[] ……
引用参数 &
算法：
void add(int a,int b,int &c) { c=a+b; }
程序：
void add(int a,int b,int *p_c){ *p_c=a+b; }
第四节 算法的描述及分析

一、有关算法的概念

算法：特定问题求解步骤的一种描述。
1)有穷性　 2)确定性　 3)可行性

二、算法设计的要求

好算法：
　1)正确性　2)可读性　3)健壮性　4)高效，低存储

三、时间复杂度

事前估算：问题的规模，语言的效率，机器的速度
时间复杂度：在指定的规模下，基本操作重复执行的次数。
n：问题的规模。
　f(n)：基本操作执行的次数　
T(n)=O(f(n)) 渐进时间复杂度(时间复杂度)
例：求两个方阵的乘积 C＝AB
void MatrixMul(float a[][n],float b[][n],float c[][n])
{ int i,j,k;
for(i=0; i<n; i++) // n+1
for(j=0; j<n; j++) // n(n+1)
{ c[i][j]=0; // nn
for(k=0; k<n; k++) // nn(n+1)
c[i][j]+ = a[i][k] * b[k][j]; // nnn
}
}
时间复杂度：
一般情况下，对循环语句只需考虑循环体中语句的执行次数，可以忽略循环体中步长加1、终值判断、控制转移等成分。
　 最好/最差/平均时间复杂度的示例：
例：在数组A[n]中查找值为k的元素。
for(i=0; i<n-1; i++)
if(A[i]==k) return i;

四、常见时间复杂度

按数量级递增排序：

< < < < <
< < <
将指数时间算法改进为多项式时间算法：伟大的成就。

五、空间复杂度

实现算法所需的辅助存储空间的大小。
　　S(n)=O(f(n)) 按最坏情况分析。

六、算法举例

例1：以下程序在数组中找出最大值和最小值
void MaxMin(int A[], int n)
{ int max, min, i;
max=min=A[0];
for(i=1; i<n; i++)
if(A[i]>max) max=A[i];
else if(A[i]<min) min=A[i];
printf(“max=%d, min=%d\n”, max, min);
}
若数组为递减排列，比较次数是多少？
if(A[i]>max)：n-1次
if(A[i]<min): n-1次
若数组为递增排列，比较次数是多少？
if(A[i]>max)：n-1次
if(A[i]<min): 0次
例2：计算f(x)=a0+a1x+a2x2+…+anxn
解法一：先将x的幂存于power[]，再分别乘以相应系数。
float eval(float coef[],int n,float x)
{ float power[MAX], f;
int i;
for(power[0]=1,i=1;i<=n;i++)
power[i]=x*power[i-1];
for(f=0,i=0;i<=n;i++)
f+=coef[i]power[i];
return(f);
}
解法二：f(x)=a0+(a1+(a2+……+(an-1+anx)x)… x)x
f(x)=a0+(a1+(a2+(a3+(a4+a5x)x)x)x)x
float eval(float coef[],int n,float x)
{ int i; float f;
for(f=coef[n],i=n-1;i>=0;i–)
f=fx+coef[i];
return(f);
}

五、思考题

1、问：“s=s+ij;”的执行次数？时间复杂度？
for(i=1;i<=n;i++)
if(5i<=n)
for(j=5i;j<=n;j++)
s=s+ij;
2、问：“a[i][j]=x;”的执行次数？时间复杂度？
for(i=0; i<n; i++)
for(j=0; j<=i; j++) a[i][j]=x;

第二章 线性表

线性结构：在数据元素的非空集中，
①存在唯一的一个首元素，
②存在唯一的一个末元素，
③除首元素外每个元素均只有一个直接前驱，
④除末元素外每个元素均只有一个直接后继。

第一节 逻辑结构

形式定义：
Linear_list=(D，S，P)
D = {ai| ai∈ElemSet, i=0,1,2,…,n-1}
S = {<ai-1,ai>| ai-1,ai∈D, i=1,2,…,n-1}
　　<ai-1,ai>为序偶，表示前后关系
基本操作P：
①插入、删除、修改，存取、遍历、查找。
void ListAppend(List L, Elem e) ;
void ListDelete(List L, int i) ;
int SetElem(List L, int i, Elem e);
int GetElem(List L, int i, Elem &e);
int ListLength(List L);
void ListPrint(List L);
int LocateElem(List L, Elem e);
②合并、分解、排序
基本操作的用途：
集合的并、交、差运算
　　 有序线性表的合并、多项式的运算
例：利用线性表LA和LB分别表示集合A和B，求A=A∪B。
void union(List &La，List Lb)
{ int La_len, Lb_len;
La_len=ListLength(La); // 计算表长
Lb_len=ListLength(Lb);
for(i=1; i<=Lb_len; i++)
{ GetElem(Lb, i, e); // 取Lb的第i个元素
if(!LocateElem(La, e)) // 在La中查找e
ListAppend(La, e); // 在La中插入e
}
}

第二节 顺序存储结构

一、概念

逻辑结构中的“前后关系”：物理结构中的“相邻关系”

loc(ai)=loc(a0)+i*sizeof(单个数据元素)
静态顺序存储结构：一维数组。
　　　　 注意：第i个元素的下标是i-1
　　动态顺序存储结构
#define LIST_INIT_SIZE 100
#define LIST_INCREMENT 10 // 存储空间的分配增量
typedef struct
{ ElemType *elem;
int length; //当前表长
int listsize; //当前已分配的存储空间
}SqList;

二、基本操作：

1、在ai之前插入x：
a0 a1 … ai-1 ai … … an-1
如何移动元素？
a0 a1 … ai-1 x ai … … an-1
void SqList_Delete(SqList A, int i)
{ for(j=i+1; j<A.length; j++)
A.elem[j-1] = A.elem[j];
A.length–;
}

三、效率分析

插入、删除时，大量时间用在移动元素上。
设插入位置为等概率事件，时间复杂度？
例1：增序顺序表的合并，设其中无相同元素
Status SqList_Merge(SqList La,SqList Lb,SqList &Lc)
{ ElemType *pa,*pb,*pc,pa_last,pb_last;
Lc.listsize=Lc.length=La.length+Lb.length;
Lc.elem=(ElemType)malloc(Lc.listsizesizeof(ElemType));
if(!Lc.elem) return ERROR;
pa=La.elem; pb=Lb.elem; pc=Lc.elem;
pa_last=La.elem+La.length-1;
pb_last=Lb.elem+Lb.length-1;
while(pa<=pa_last && pb<=pb_last)
if(*pa<=*pb) { *pc=*pa; pc++; pa++; }
else { *pc=*pb; pc++; pb++; }
while(pa<=pa_last) { *pc=*pa; pc++; pa++; }
while(pb<=pb_last) { *pc=*pb; pc++; pb++; }
return OK;
}
时间复杂度？
现实意义：数据库与日志文件的合并。
例2：无序顺序表的并集A∪B
例3：无序顺序表的交集A∩B
例4：无序顺序表的逆序
例5：剔除顺序表中的某种元素
剔除顺序表中的所有0元素，要求较高效率。
1 2 0 3 4 0 0 0 5 6 7 0 0 8 9
=> 1 2 3 4 5 6 7 8 9
void del(int A[],int n)
{ int i,k; // k是0元素的个数
for(k=0,i=0; i<n; i++)
if(A[i]==0) { k++; n–; }
else A[i-k] = A[i];
}

第三节 线性动态链表

一、概念

每个元素除存储自身信息外，还需存储其后继元素的信息。
　　


结点、指针域、指针(链)
链表、线性链表、头指针

二、动态链表结构
typedef struct LNode
{ ElemType data;
struct LNode next;
}LNODE;
申请结点空间：
LNODE p;
p=(LNODE )malloc(sizeof(LNODE));
释放结点空间:
free§;
1、插入结点
在p之后插入新结点q：
q->next=p->next; p->next=q;
在p之前插入？
　 时间复杂度？
各种插入方法：
①首插：插入在首结点前；
②尾插：入在尾结点后。
③有序插：保持结点的顺序，插在表中间；
编程细节：
①首插：修改头指针
②尾插：链表为空时，修改头指针。
③有序插：链表为空时，修改头指针。
链表不空时，可能修改头指针
// 首插
LNODE * LinkList_InsertBeforeHead(LNODE *head, LNODE *newp)
{ newp->next=head; return(newp); }
// 遍历打印
void LinkList_Print(LNODE *head)
{ LNODE *p;
for(p=head; p; p=p->next)
printf(“…”,p->data);
}
// 尾插
LNODE * LinkList_InsertAfterTail(LNODE *head, LNODE *newp)
{ LNODE *p;
if(headNULL) { newp->next=NULL; return(newp); }
for(p=head->next; p->next; p=p->next);
newp->next=NULL; p->next=p;
return(head);
}
简化程序细节的方法：特殊头结点
// 首插（有特殊头结点）
void LinkList_InsertBeforeHead(LNODE *head, LNODE *newp)
{ newp->next=head->next;
head->next=newp;
}
// 尾插（有特殊头结点）
void LinkList_InsertAfterTail(LNODE *head, LNODE newp)
{ LNODE p;
for(p=head; p->next; p=p->next);
newp->next=NULL; p->next=p;
}
2、删除结点
删除p的后继结点：
q=p->next; p->next=q->next; free(q);
删除p？
时间复杂度？
各种删除方法：
①首删除：
②尾删除： 思考
③查找删除：思考
// 首删除（有特殊头结点）
void LinkList_DeleteHead(LNODE *head)
{ LNODE *p;
if(head->nextNULL) return;
p=head->next; head->next=p->next;
free(q);
}

三、单个链表的例程（设以下链表有特殊头结点）

例1、按序号查找：取链表第i个结点的数据元素。i∈[1,n]
// 注意计数次数的边界条件
Status LinkList_GetElemBySID(LNODE *head,int i,ElemType &e)
{ LNODE *p; int j;
for(p=head->next,j=1; p && j<i; j++) p=p->next;
if(pNULL) return ERROR;
e=p->data; return OK;
}
例2、按值查找：取链表中值为e的结点的地址。
LNODE * LinkList_GetElemByValue(LNODE *head, ElemType e)
{ LNODE *p;
for(p=head->next; p; p=p->next)
if(p->datae) break;
return§;
}
例3、释放链表中所有结点。
void LinkList_DeleteAll(LNODE *head)
{ LNODE *p;
while(head)
{ p=head->next; free(head); head=p; }
}
例4、复制线性链表的结点
// 适合有/无特殊头结点的链表
LNODE * LinkList_Copy(LNODE *L)
{ LNODE *head=NULL,*p,*newp,*tail;
if(!L) return(NULL);
for(p=L; p; p=p->next)
{ newp=(LNODE *)malloc(sizeof(LNODE));
if(headNULL) head=tail=newp;
else { tail->next=newp; tail=newp; }
newp->data=p->data;
}
tail->next=NULL; return(head);
}
例5、线性链表的逆序
LNODE * LinkList_Reverse(LNODE *head)　　
{ LNODE *newhead,*p;
newhead=(LNODE *)malloc(sizeof(LNODE));
newhead->next=NULL;
while(head->next!=NULL)
{ p=head->next; head->next=p->next; //卸下
p->next=newhead->next; newhead->next=p; //安装
}
free(Head);
return(newhead);
}
例6、利用线性表的基本运算，实现清除L中多余的重复节点。
3 5 2 5 5 5 3 5 6
=> 3 5 2 6
void LinkList_Purge(LNODE *head)
{ LNODE *p, *q, *prev_q;
for(p=head->next; p; p=p->next)
for(prev_q=p,q=p->next; q; )
if(p->dataq->data)
{ prev_q=q->next; free(q); q=prev_q->next; }
else
{ prev_q=q; q=q->next; }
}

四、多个链表之间的例程（设以下链表有特殊头结点）

例1、增序线性链表的合并，设其中无相同元素。
//破坏La和Lb，用La和Lb的结点组合Lc
LNODE *LinkList_Merge(LNODE *La,LNODE *Lb)
{ LNode *pa,*pb,*pctail,*Lc;
Lc=pctail=La; // Lc的头结点是原La的头结点
pa=La->next; pb=Lb->next; free(Lb);
while(pa!=NULL && pb!=NULL)
if(pa->data <= pb->data)
　 { pctail->next=pa; pctail=pa; pa=pa->next; }
　 else { pctail->next=pb; pctail=pb; pb=pb->next; }
if(pa!=NULL) pctail->next=pa;
else pctail->next=pb;
return(Lc);
}
例2、无序线性链表的交集A∩B
//不破坏La和Lb，
//新链表Lc的形成方法：向尾结点后添加结点
LNODE *LinkList_Intersection(LNODE *La,LNODE *Lb)
{ LNode *pa,*pb,*Lc,*newp,*pctail;
Lc=pctail=(LNODE *)malloc(sizeof(LNODE));
for(pa=La->next; pa; pa=pa->next)
{ for(pb=Lb->next; pb; pb=pb->next)
if(pb->data==pa->data) break;
if(pb)
{ newp=(LNODE *)malloc(sizeof(LNODE));
newp->data=pa->data;
pctail->next=newp; pctail=newp;
}
}
pctail->next=NULL;
return(Lc);
}
作业与上机：(选一)
1、A-B
2、A∪B
3、A∩B
4、(A-B)∪(B-A)

第五节 循环链表

尾结点的指针域指向首结点。
实际应用：手机菜单
遍历的终止条件？
例：La、Lb链表的合并


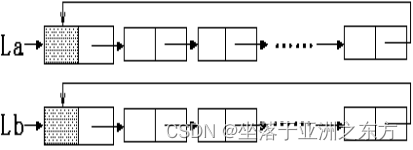
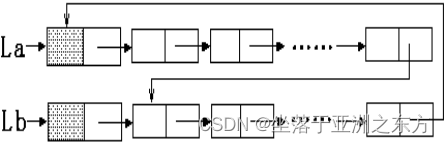
// 将Lb链表中的数据结点接在La链表末尾
void Connect(LNODE * La，LNODE * Lb)
{ LNODE *pa, *pb;
for(pa=La->next; pa->next!=La; pa=pa->next);
for(pb=Lb->next; pb->next!=Lb; pb=pb->next);
pa->next=Lb->next; pb->next=La;
free(Lb);
}

第六节 双向链表

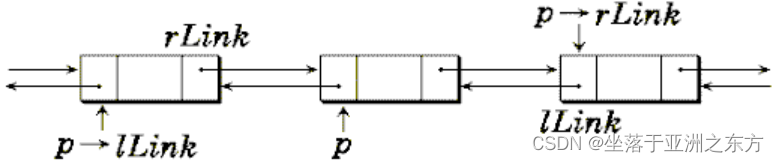
1、在p之后插入结点q
q->rLink=p->rLink; q->lLink=p;
p->rLink=q; q->rLink->lLink=q
在p之前插入结点q ?
2、删除p
(p->lLink)->rLink=p->rLink;
(p->rLink)->lLink=p->lLink;
free§;
删除p的前驱结点?
删除*p的后继结点?

第七节 实例：一元多项式的存储、运算

一、多项式的存储结构

f(x) = anxn +......+a2x2 + a1x + a0

1、顺序结构
int coef[MAX];
f(x) = 14x101+ 5x50 - 3
2、链式结构
typedef struct polynode
{ int coef;
int index;
struct node *next;
}PolyNode;
3、示例

4、结构细节设计
带特殊头结点的单向链表；
结点按指数降序排列；
特殊头结点的index域：多项式的项数。
5、程序框架设计
main()
{ PolyNode *L1,*L2;
L1=PolyNode_Create(); PolyNode_Print(L1);
L2=PolyNode_Create(); PolyNode_Print(L2);
PolyNode_Add(L1,L2); // L1+L2=>L1
PolyNode_Print(L1);
}
void PolyNode_Print(PolyNode *head)
{ PolyNode *p;
printf(“count=%d\n”,head->index); //打印项数
for(p=head->next; p; p=p->next)
printf(“coef=%d,index=%d\n”,p->coef, p->index);
}

二、以插入为基础的算法

1、将newp插入到降序链表head中
void PolyNode_Insert(PolyNode *head, PolyNode *newp);
{ PolyNode *p,pre;
// 定位
for(pre=head,p=pre->next; p; pre=p,p=p->next)
if(p->index <= newp->index) break;
if(p==NULL || p->index < newp->index) //在pre之后插入
{ newp->next=p; pre->next=newp; head->index++; }
else
{ p->coef += newp->coef; //合并同类项
free(newp);
if(p->coef==0) //删除
{ pre->next=p->next; free§; head->index–; }
}
}
2、利用PolyNode_Insert函数，建立有序链表
PolyNode *PolyNode_Create()
{ int i,count;
PolyNode *head,*newp;
scanf(“%d\n”,&count);
head=(PolyNode *)malloc(sizeof(PolyNode));
head->coef=0; head->next=NULL;
for(i=0; i<count; i++)
{ newp=(PolyNode *)malloc(sizeof(PolyNode));
scanf(“%d,%d\n”,&newp->coef,&newp->index);
PolyNode_Insert(head, newp);
}
return(head);
}
3、利用PolyNode_Insert函数，实现多项式加法
// L1+L2=>L1 不破坏L2链表
void PolyNode_Add(PolyNode *L1, PolyNode *L2)
{ NODE *p,*newp;
for(p=L2->next; p; p=p->next)
{ newp=(PolyNode )malloc(sizeof(PolyNode));
newp->coef=p->coef; newp->index=p->index;
PolyNode_Insert(L1,newp);
}
}
时间复杂度？
设L1长度为M，L2长度为N，则O(MN)。

三、两表合并算法

L1+L2=>L1 破坏L2链表
将L2中的每个结点卸下，合并到L1中




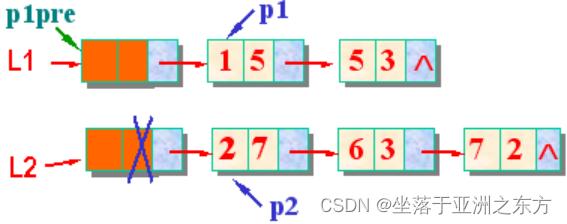
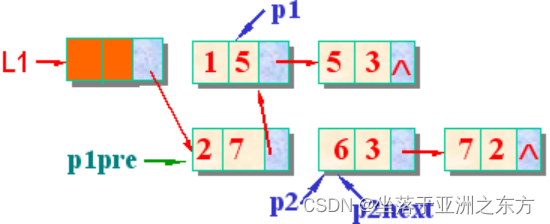
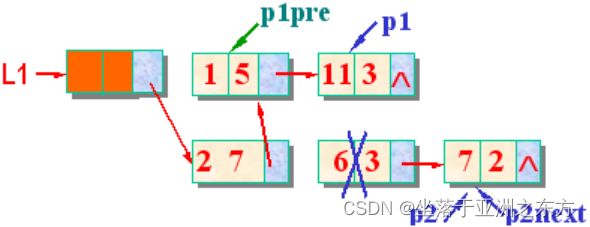
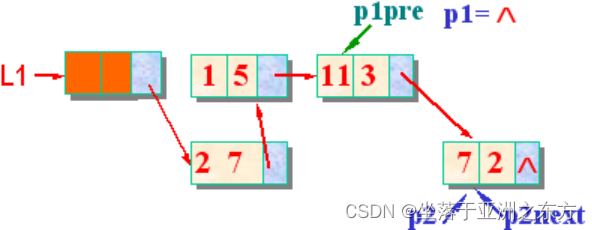
void PolyNode_Add(PolyNode *L1, PolyNode L2)
{ PolyNode p1, p1pre; // p1pre 是p1的直接前驱
PolyNode p2, p2next; // p2next是p2的直接后继
p1pre=L1; p1=L1->next; // p1指向L1中第一个数据结点
p2=L2->next; free(L2); // p2指向L2中第一个数据结点
while(p1 && p2)
{ switch(compare(p1->index, p2->index))
{ case ‘>’: // p1指数大于p2指数
p1pre=p1; p1=p1->next; break;
case ‘<’: // p1指数小于p2指数
p2next=p2->next; // 小心①：准备在p1pre后插入p2
p2->next=p1; p1pre->next=p2;
p1pre=p2; // 小心②：保持p1pre和p1的关系
p2=p2next; // p2指向下一个待合并的结点
break;
case ‘=’: // p1和p2是同类项
p1->coef+=p2->coef; // 系数合并
p2next=p2->next; free(p2); // 删除p2
p2=p2next; // p2指向下一个待合并的结点
if(pa->coef==0) // 合并后系数为0
{ p1pre->next=p1->next; free(p1); // 删除p1
p1=p1pre->next; // 保持p1pre和p1的关系
}
} // switch
} // while
if(p2) p1pre->next=p2; // 链上p2的剩余结点
}
时间复杂度？
设L1长度为M，L2长度为N，则O(M+N)。
作业与上机：(选一)
一、多项式加法、减法
二、多项式乘法:ab=>c(建立新表c)
三、任意整数的加法、乘法

第三章 栈与队列

栈与队列：限定操作的线性表。

第一节 栈

一、逻辑结构

1、栈的定义
限定只能在表的一端进行插入、删除的线性表。

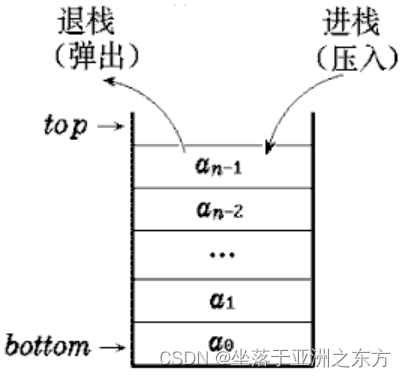
　　栈顶top，栈底bottom。
　　后进先出LIFO表(Last In First Out)
实例：“进制数转换”、“表达式求值”、“函数调用关系”、“括号匹配问题”、“汉诺塔问题”、“迷宫问题”……

2、基本操作

进栈Push/出栈Pop
取栈顶元素GetTop
判别栈空StackEmpty/栈满StackFull

3、栈的应用背景

许多问题的求解分为若干步骤，而当前步骤的解答，是建立在后继步骤的解答基础上的。=》问题分解的步骤和求解的步骤次序恰好相反。

二、顺序存储结构

动态顺序存储结构：存储空间随栈的大小而变化。

SqStack S; //定义一个栈结构

1、初始化栈

Status SqStack_Init(SqStack &S)
{ S.base=malloc(STACK_INIT_SIZE*sizeof(ElemType));
if(!S.base) return(OVERFLOW);
S.top=S.base; S.stacksize=STACK_INIT_SIZE;
return(OK);
}
栈空： S.topS.base
栈满： S.topS.base+S.stacksize

2、进栈

Status SqStack_Push(SqStack &S,ElemType e)
{ if(S.top==S.base+S.stacksize) return(OVERFLOW);
S.top=e; S.top++;
return(OK);
}

3、出栈算法

Status SqStack_Pop(SqStack &S,ElemType &e)
{ if(S.top==S.base) return(UNDERFLOW);
S.top–; e=S.top;
return(OK);
}
缺点：空间浪费
思考：二栈合用同一顺序空间？

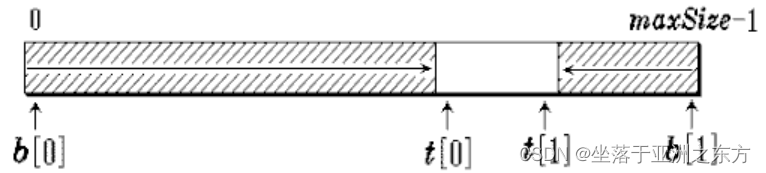
#define maxsize=100
int stack[maxsize], top0=0, top1=maxsize-1;

三、链栈

LinkStack S;
初始化: S.topNULL; S.stacksize0
栈 空：S.top==NULL
栈 满：系统内存不够

1、进栈

Status LinkStack_Push(LinkStack &S，ElemType e)
{ LinkNode *p;
p=(LinkNode *)malloc(sizeof(LinkNode));
if(p==NULL) return(OVERFLOW); //上溢
p->data=e;
p->link=S.top; S.top=p;
return(OK);
}

2、出栈

Status LinkStack_Pop(LinkStack &S,ElemType &e)
{ LinkNode *p;
if(S.top==NULL) return(UNDERFLOW);
p=S.top;
e=S.top->data; S.top=S.top->link; free§;
return(OK);
}

3、特殊头结点的讨论

进栈、出栈是最常用的操作
=》链栈的头指针频繁变更
=》参数传递的负担
=》应约定链栈具有特殊头结点。

第二节 栈的应用

1、函数调用栈

f(n)=f(n-1)+f(n-2)

2、将十进制数转换为八进制数。

例如 (1348)10=(2504)8，除8取余的过程：

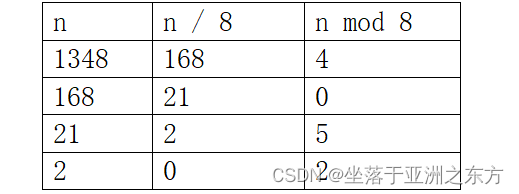
void Conversion(int dec,int oct[])
{ InitStack(S);
for(; dec!=0; dec=dec/8)
push(S, dec%8); /* 进栈次序是个位、十位… /
for(i=0; !StackEmpty(S); i++)
oct[i]=pop(S); / 先出栈者是高位，最后是个位 */
}

3、括号匹配的检验

Equal( "((a)(b)) " ) : 0
Equal( “(((a)(b))” ) : 1
Equal( “((a)(b)))” ) : -1
int Equal(char s[])
{ int i=0;
for(i=0; s[i]; i++)
switch(s[i])
{ case ‘(’: push(s[i]); break;
case ‘)’: if(StackEmpty(S)) return(-1); // )多
pop(); break;
}
if(!StackEmpty(S)) return(1); // (多
return(0); // 完全匹配
}

4、进栈出栈的组合问题

已知操作次序：push(1); pop(); push(2); push(3); pop(); pop( ); push(4); pop( ); 请写出出栈序列。

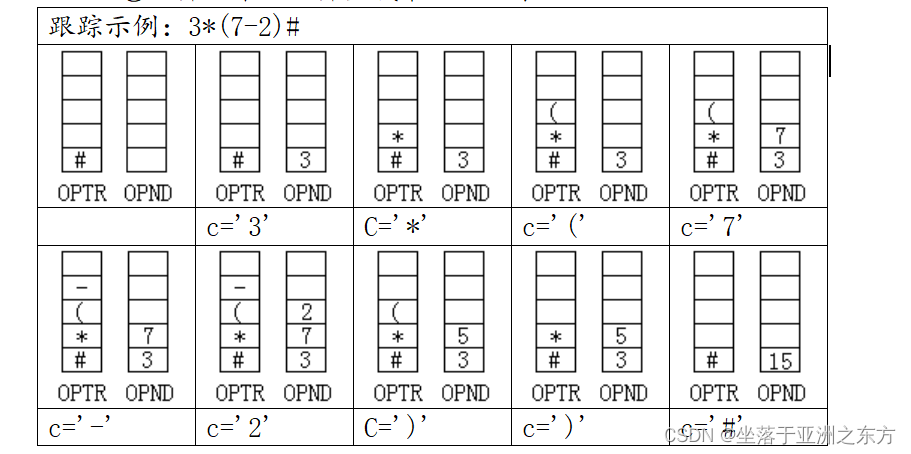
5、中缀表达式求值的算法

如： 1 + 2 *（3 + 4 *（5 + 6））
分析：先乘除，后加减；从左到右；先括号内，再括号外。

①一个运算是否立即执行？必须和“上一个运算符”比较优先级。
3 * 5 + 2
3 - 5 * 2 + 8
②“上一个运算符”存于何处？ 运算符栈
③对应的运算数存于何处？ 运算数栈
④为保证第一个运算符有“上一个运算符”： Push(OPTR,‘#’)
为保证最后一个运算符能被执行： “3*5+2#”
#：优先级最低的运算符。
⑤运算结果：运算数栈最后的元素。

charStack：
类型定义：
基本函数：InitStack1(charStack *);
char GetTop1(charStack *);
void Push1(charStack *, char);
char Pop1(charStack *);
intStack:
类型定义：
基本函数：InitStack2(intStack *);
int GetTop2 (intStack *);
void Push2(intStack , int);
int Pop2(intStack );
float MidExpression_Eval(char Express[]) // Express[]:"35+2#"
{ int i=0; char c,pre_op;
charStack OPTR; intStack OPND;
InitStack1(&OPTR); Push1(&OPTR,‘#’); / 运算符栈 /
InitStack2(&OPND); / 运算数栈 /
while(Express[i]!=‘#’ || GetTop1(&OPTR)!=‘#’)
{ c=Express[i];
if(!InOPTR©)
{ Push2(&OPND, c-‘0’); i++; } / getnum(Express,&i) /
else
{ pre_op=GetTop1(&OPTR);
switch(Precede(pre_op, c))
{ case ‘<’: // pre_op < c
Push1(&OPTR,c); i++; break;
case ‘=’:
Pop1 (&OPTR); i++; break;
case ‘>’: // pre_op > c 执行pre_op
b=Pop2(&OPND); a=Pop2(&OPND); Pop1(&OPTR);
Push2(&OPND,Operate(a,pre_op,b));
}
}
return(GetTop2(&OPND));
}
// 优先级的处理技巧
+ - * / ( ) #
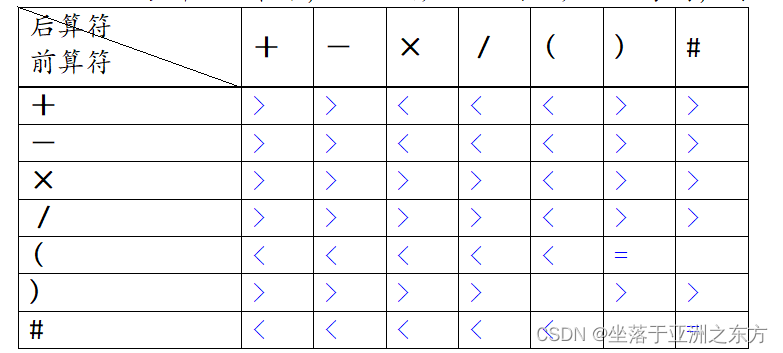
int priority[7][7]={{‘>’, ‘>’, ‘<’, ‘<’, ‘<’, ‘>’, ‘>’}, // +
{‘>’, ‘>’, ‘<’, ‘<’, ‘<’, ‘>’, ‘>’}, // -
{‘>’, ‘>’, ‘>’, ‘>’, ‘<’, ‘>’, ‘>’}, // *
{‘>’, ‘>’, ‘>’, ‘>’, ‘<’, ‘>’, ‘>’}, // /
{‘<’, ‘<’, ‘<’, ‘<’, ‘<’, ‘=’, }, // (
{‘>’, ‘>’, ‘>’, ‘>’, , ‘>’, ‘>’}, // )
{‘<’, ‘<’, ‘<’, ‘<’, ‘<’, , ‘=’}, // #
}
int OpID(char op)
{ switch (op)
{ case ‘+’ : return(0);
case ‘-’ : return(1);
case '’ : return(2);
case ‘/’ : return(3);
case ‘(’ : return(4);
case ‘)’ : return(5);
case ‘#’ : return(6);
}
}
char Precede(char op1, char op2)
{ return(priority[OpID(op1)][OpID(op2)]); }

测试案例：“#”， “3#”，“3+5#”，“3+5+2#”
“35+2#"， "3+52#”，“(3+5)2#"，
"(3+5)(2+1)#”，“((3+5)/2+1)*2#” …………
作业与上机：
1、表达式求值

第三节 队列

一、逻辑结构

　　只能在一端(队尾rear)插入，在另一端(队头front)删除的线性表。
　　先进先出表FIFO(First In First Out)
基本操作：进/出队列
判别队列满/空

队列的应用背景：排队模型。排队问题无处不在，各种服务行业、甚至生产管理中都存在排队问题。

二、链式存储结构

LinkQueue Q;
初始化空队列： Q.frontNULL Q.rearNULL

1、入队列

Status LinkQueue_Enter(LinkQueue &Q, ElemType e)
{ QueueNode *p;
p=(QueueNode *)malloc(sizeof(QueueNode));
if(!p) return(OVERFLOW);
p->data=e; p->link=NULL;
if(Q.front==NULL) Q.front=Q.rear=p;
else { Q.rear->link=p; Q.rear=p; }
return(OK);
}

2、出队列

Status LinkQueue_Leave(LinkQueue &Q,ElemType &e)
{ QueueNode *p;
if(Q.frontNULL) return(UNDERFLOW);
p=Q.front; Q.front=p->link;
if(Q.rearp) Q.rear=NULL;
e=p->data; free§;
return(OK);
}

3、销毁队列

void LinkQueue_Destroy(LinkQueue &Q)
{ QueueNode *p;
while(Q.front)
{ p=Q.front;
Q.front=p->link;
free§;
}
Q.rear=NULL;
}

三、顺序存储结构

动态顺序存储结构：

SqQueue Q; //定义一个队列结构
rear为下一个进队列元素的位置。
front在队列不空时，指向首元素；
在队列为空时，等于rear。

1、初始化队列

Status SqQueue_Init(SqQueue &Q)
{ Q.base=malloc(QUEUE_SIZEsizeof(ElemType));
if(!Q.base) return(OVERFLOW);
Q.front=Q.rear=0;
return(OK);
}
队列空： Q.front==Q.rear
进队列：(Q.base+Q.rear)=e; Q.rear++;
出队列：e=*(Q.base+Q.front); Q.front++;

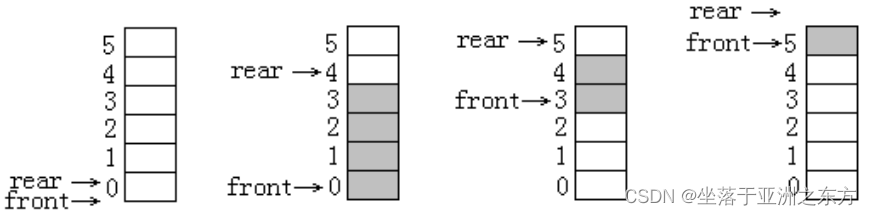
队列满： Q.rearQUEUE_SIZE
=》假溢出
进队列：Q.rear =(Q.rear +1) % QUEUE_SIZE
出队列：Q.front=(Q.front+1) % QUEUE_SIZE
队列空：Q.frontQ.rear
当队列中有QUEUE_SIZE个元素时：
Q.front==Q.rear
=》必须浪费一个结点空间
队列满：(Q.rear +1) % QUEUE_SIZE == Q.front

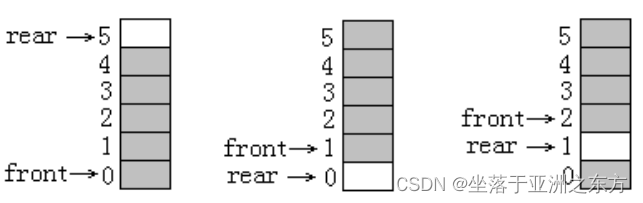
2、入队列

Status SqQueue_Enter(SqQueue &Q,ElemType e)
{ if((Q.rear +1) % QUEUE_SIZE==Q.front) return(OVERFLOW);
*(Q.base+Q.rear)=e;
Q.rear=(Q.rear +1) % QUEUE_SIZE;
return(OK);
}

3、出队列

Status SqQueue_Leave(SqQueue &Q,ElemType &e)
{ if(Q.rear==Q.front) return(UNDERFLOW);
e=*(Q.base+Q.front);
Q.front=(Q.front+1) % QUEUE_SIZE;
return(OK);
}

4、元素计数

(Q.rear-Q.front+QUEUE_SIZE)% QUEUE_SIZE
值的范围0 …… QUEUE_SIZE-1
思考：一定要浪费一个结点空间？
利用一个标志变量Q.flag (0:非满，1:非空)。

int Empty(SqQueue Q)
{ if(Q.frontQ.rear && Q.flag0) return(1);
return(0);
}
int Full(SqQueue Q)
{ if(Q.frontQ.rear && Q.flag1) return(1);
return(0);
}

1、初始化队列

Status SqQueue_Init(SqQueue &Q)
{ Q.front=Q.rear=0; Q.flag=0; }

2、入队列

Status SqQueue_Enter(SqQueue &Q,ElemType e)
{ if(Full(Q)) return(OVERFLOW);
…………
Q.flag=1; //非空
return(OK);
}

3、出队列

Status SqQueue_Leave(SqQueue &Q,ElemType &e)
{ if(Empty(Q)) return(UNDERFLOW);
…………;
Q.flag=0; //非满
return(OK);
}
第四节 队列的实例：离散事件的模拟

一、排队问题

加油站的问题：
一个加油站只有一台加油机,平均为每辆车加油需要5分钟,假定一个小时内,有20辆车随机进入加油站加油,计算每辆车的平均等待时间.
银行营业所应设置几个柜台？
1、设置N柜台时，计算顾客的平均等待时间；
2、选择合适的N值。

二、两个栈组合出一个队列

制定两个栈与一个队列的对应规则：

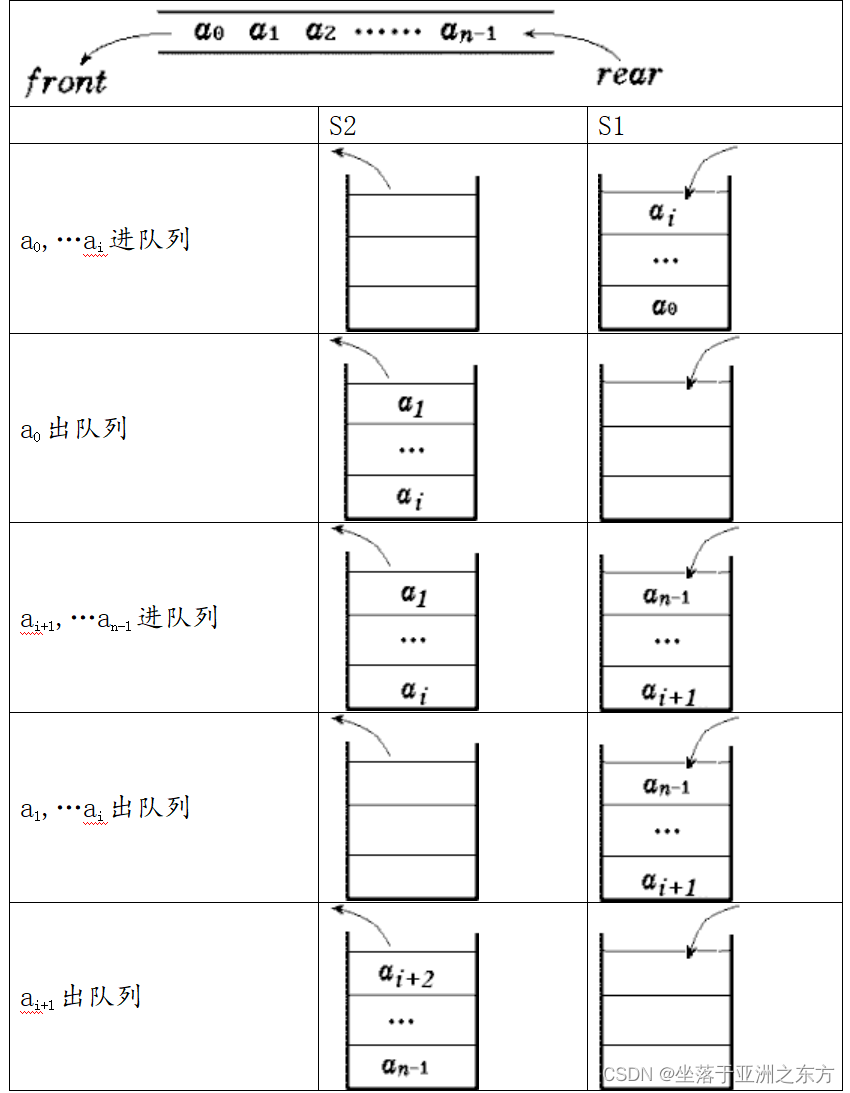
stack s1,s2;
void Enter(ElemType e)
{ Push(s1,e); }

ElemType Leave()
{ ElemType e;
if( !Empty(s2) ) return( Pop(s2) );
while( !Empty(s1) )
Push(s2, Pop(s1));
return( Pop(s2) );
}