1. 文章简介

• 标题：On the Sentence Embeddings from Pre-trained Language Models
• 作者：Bohan Li, Hao Zhou, Junxian He, Mingxuan Wang, Yiming Yang, Lei Li
• 日期：2020
• 期刊：arxiv preprint

2. 文章概括

  近期的一些研究表明，传统的BERT模型产生的词向量空间成anisotropic（各向异性），在语义相似度任务上表现不好，甚至低于GloVe方法。为此，文章提出了BERT-flow，一种基于Gaussian latent变换的BERT系列模型，可以有效地将BERT产生的词向量空间映射到一个standard Gaussian latent space。BERT-flow在STS语义相似度任务上表现超过SOTA，且实验表明BERT-flow要优于其它已有的针对各向异性的解决方法。

3 文章重点技术

3.1 BERT模型的语义相似度能力分析

  首先简要回顾下BERT模型[1]。BERT模型采用了MLM和NSP两种目标来训练模型。所谓MLM，即Masked Language Modeling（掩码语言模型），BERT会随机的对15%的词表单词进行掩码，然后在实际训练时尝试根据被掩码单词的上下文预测这些掩码。具体公示可表示为$p(\overline{x}|\hat{x})={\sum }_{t=1}^T{m}_{t}p(x_t|c_t)$，其中${\hat{x}}_t$表示被掩码的序列，$\overline{x}$表示被掩码的tokens，当$x_t$被掩码时$m_t=1$，否则为$0$，上下文$c_t=\hat{x}$。公示中的条件概率$p(x_t|\hat{x})$可由softmax预测：$$p(x|\hat{x})=\frac{\exp h_c^T{w}_x}{{\sum }_{x^{\prime }}\exp h_c^T{w}_{x^{\prime }}}\text{\hspace{1em}(1)}$$，其中$h_c$时上下文的嵌入表示，由Transformer学习得到，$w_x$为token $x$对应的词向量。
  为了比较BERT的句向量相似度，我们可考虑$h_c^T{h}_{c^{\prime }}$。但上式中，没有显式出现$h_c^T{h}_{c^{\prime }}$，为此我们考虑$h_c^T{w}_x$，即上下文和单词嵌入之间的点积。根据Yang[2]，可以通过下式来近似$h_c^T{w}_x$: $$h_c^T{w}_x\approx \log p^{\ast }(x|c)+{\lambda }_c=PMI(x,c)+\log p(x)+{\lambda }_c$$，其中$PMI(x,c)=\log \frac{p(x,c)}{p(x)p(c)}$表示$x$个$c$之间的逐点互信息(Pointwise mutual information)，常被用来近似单词级别的语义相似，可以视为$x,c$同时出现的概率除以各自单独出现的概率，再取对数;$\log p(x)$表示单词项; ${\lambda }_c$表示上下文项。由此近似表达式我们可以看出，通过计算$h_c^T{w}_x$来估计语义相似度是有意义的。
  在BERT的预训练阶段，任意两个上下文$c,c^{\prime }$的语义关系是可以通过它们各自和单词之间的关系来推断的。事实上，如果$c,c^{\prime }$和相同的单词$w$经常一起出现，那么它们很可能语义相似。如果$c,x$同时出现，那么$h_c,w_x$会比较接近，再由(1)式的正则项，我们有对其它$x^{\prime }$，$h_c,w_x^{\prime }$会远离；同理, 如果$c^{\prime },x^{\prime }$同时出现，则$h_c^{\prime },w_x^{\prime }$会比较接近, $h_c^{\prime },w_x$会远离。故而我们得到$h_c^{\prime },h_c$会远离。总结下：即对不同的单词$x,x^{\prime }$，它们的上下文$h_c,h_c^{\prime }$也会比较远。
  按照上述推理，上下文之间的更新会彼此影响：$h_c$的更新可能会影响$h_c^{\prime }$，同理$h_c^{\prime }$的更新可能会影响$h_c^{\prime \prime }$。也就是说，上下文嵌入之间通过某种高阶的并现关系互相影响。

3.2 Anistropic各向异性

  文章尝试解释为什么BERT在语义相似问题上的表现不好。文章主要给出以下两点观测：

• 单词频次会使嵌入空间发生偏移：文章计算了BERT单词嵌的平均l2范数。如下表所示，单词的频次越高，平均l2范数越小。说明BERT的嵌入空间很可能被单词频次所影响，从而造成上下文嵌入可能会被单词频次信息污染。
  
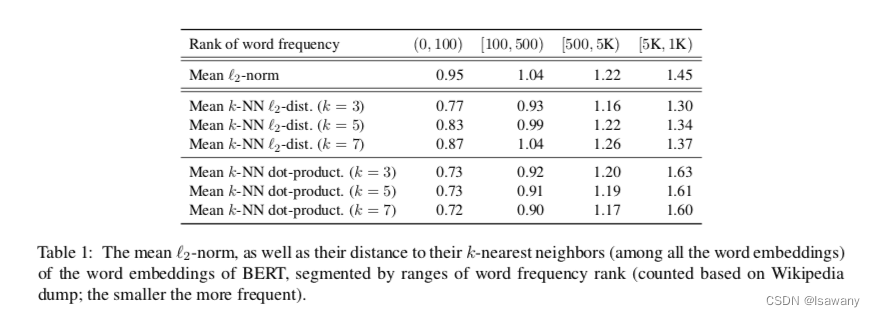
• 低频的单词在嵌入空间发散：文章计算了单词嵌入与其$k$个最近的单词嵌入之间的平均l2距离和点积，如上表所示，单词频次越低，单词和其近邻的l2距离/点积越大，说明距离越远。即频次地的单词可能会稀疏发散。这种发散性可能会造成低频次单词在高维空间中间存在"holes"，而BERT如果采用avg词向量方式表示句向量时，这些"holes"会印象影响嵌入空间的凸性，从而影响句向量的表达。

3.3 BERT-flow

  针对上述anistropy，文章提出一种校准方法BERT-flow：利用一个可逆变换将BERT的嵌入空间转化为一个标准高斯潜空间(standard Gaussian latent space，SGLS)。
  SGLS可以满足各向同性(isotropic)。事实上，一个SGLS的概率密度在各个角度上都是一致的，如果我们将SGLS的样本的2范数标准化为1 ，则样本服从一个高阶单位圆的均匀分布。将嵌入空间转化为一个各向同性的空间之后，我们可以压扁嵌入空间的较大的特征值（研究表明这些较大的特征向量很可能和单词频率有关），从而降低单词频率对嵌入空间的影响。此外，SGLS不存在holes，从而可以解决在这些holes附近句向量定义不好的问题。

3.4 Flow-based model

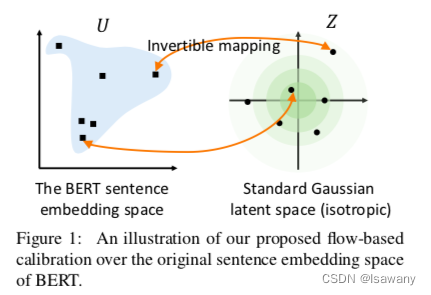
  为了得到上述的SGLS，我们希望建立一个从latent space $\mathcal{Z}$（即SGLS）到观测空间$\mathcal{U}$（即BERT嵌入空间）的可逆变换，如下图所示。具体如下：$$z\sim p_{\mathcal{Z}}(z),u=f_{\varphi }(z)$$，其中$f$为我们要找的可逆变换。根据变量变换理论，我们有$$p_{\mathcal{U}}(u)=p_{\mathcal{Z}}(f_{\varphi }^{-1}(u))|det\frac{\partial f_{\varphi }^{-1}(u)}{\partial u}|$$。

  最终得到模型要最大化似然函数$$ma{x}_{\varphi }{\mathbb{E}}_{u=BERT(sentence),sentence\sim \mathcal{D}}log{p}_z(f_{\varphi }^{-1}(u))+\log |det\frac{\partial f_{\varphi }^{-1}(u)}{\partial u}|$$，其中$\mathcal{D}$表示句子数据集。训练过程我们只训练flow的参数，即$f_{\varphi }^{-1}$部分，将BERT的参数冻结。为了得到$f_{\varphi }^{-1}$，文章参考Dinh等人的神经网络框架，保证$f_{\varphi }$是可逆的。

4. 文章亮点

  文章论证了BERT在语义相似度任务上表现较差的原因，且提出了一种可以解决BERT各向异性的方案“BERT-flow“。BERT-flow在多个STS数据集上表现超过SBERT[2]等模型，得到了一种更接近于Golden standard的嵌入空间。
  实验表明，文章提出的BERT-flow方法相比于标准正则化（计算嵌入的均值方差之后正则）和NATSV（将Top特征值消除）方法相比效果更好，成为了解决BERT各向异性问题的SOTA方案。

5. 原文传送门

On the Sentence Embeddings from Pre-trained Language Model

6. References

[1] 论文笔记–BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding
[2] Breaking the Softmax Bottleneck: A High-Rank RNN Language Model
[3] 论文笔记–Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks