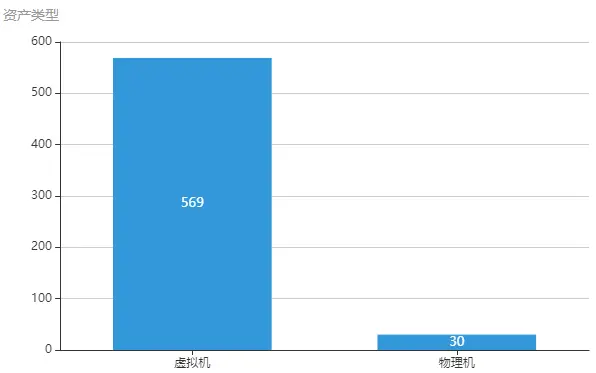
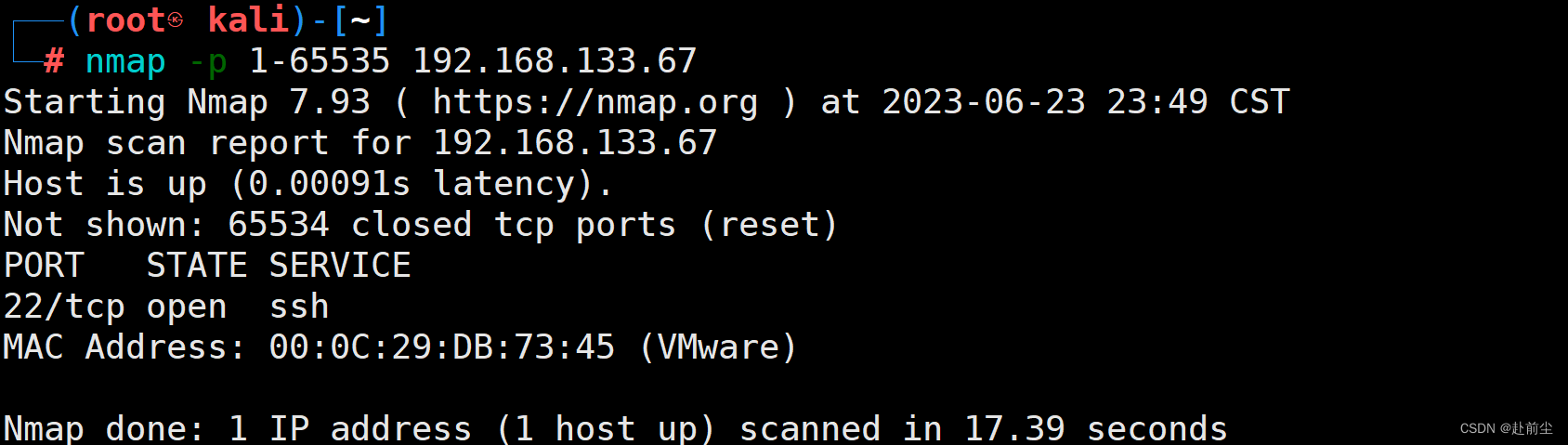
4.A
A. 不是简单路径的话，有环，去环路径会更短
B. 适合的 弗洛伊德算法才不适合
C. 本来就是
D 2X2矩阵拓展到3X3矩阵 再扩大 若是子集 即加入新顶点后，最短路径都没有变，错

5.B
本题用弗洛伊德更合适 但这道题只需全部代入求最短就好

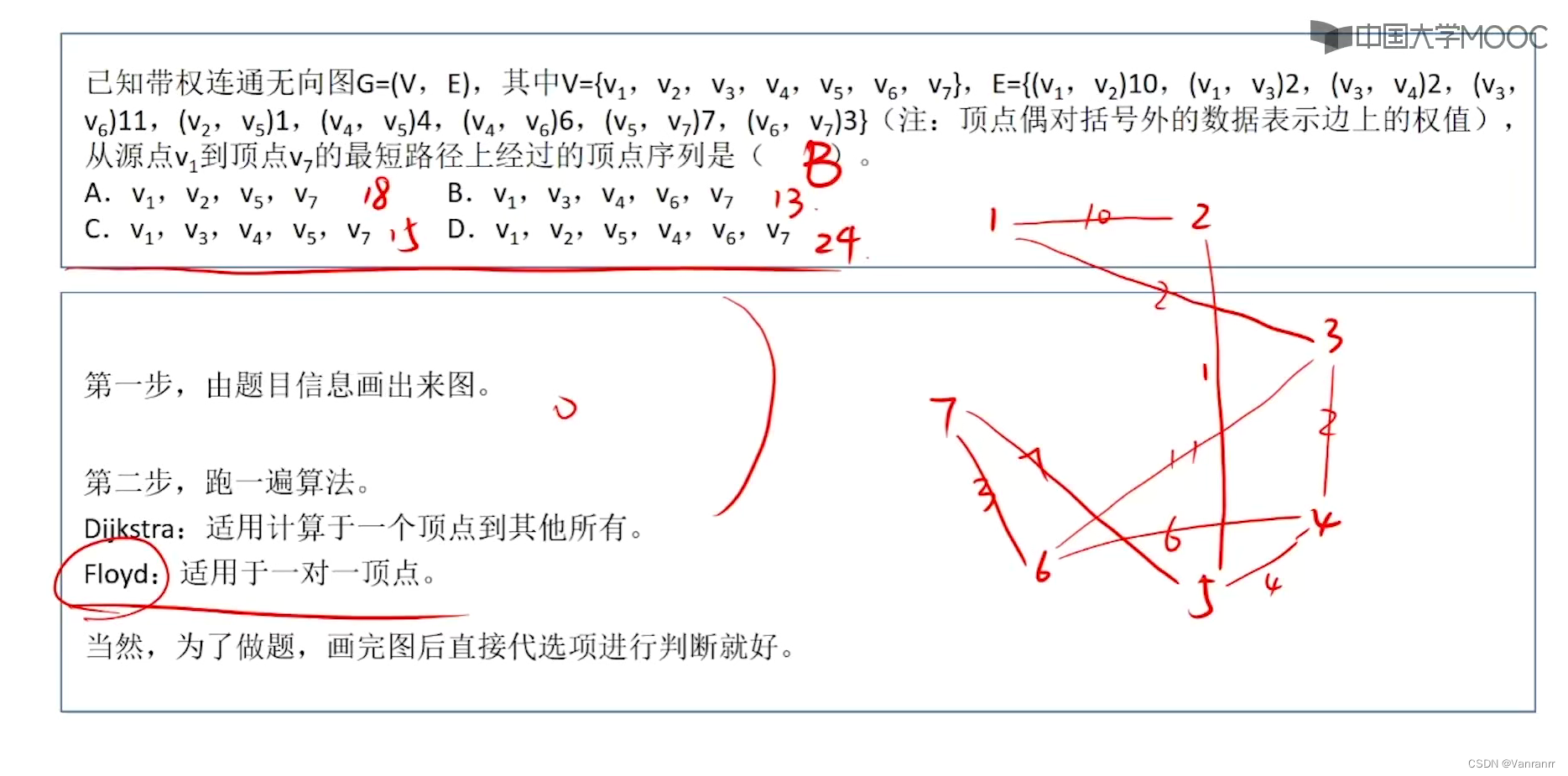
6.A
I. 深搜会入栈
II 寻找一个工程合理的推进顺序 找不到拓扑排序就是有环（原理？）
III 最短路径两种算法和有环无环无关 但不是说，弗洛伊德不用一回路吗？
IV 有争议

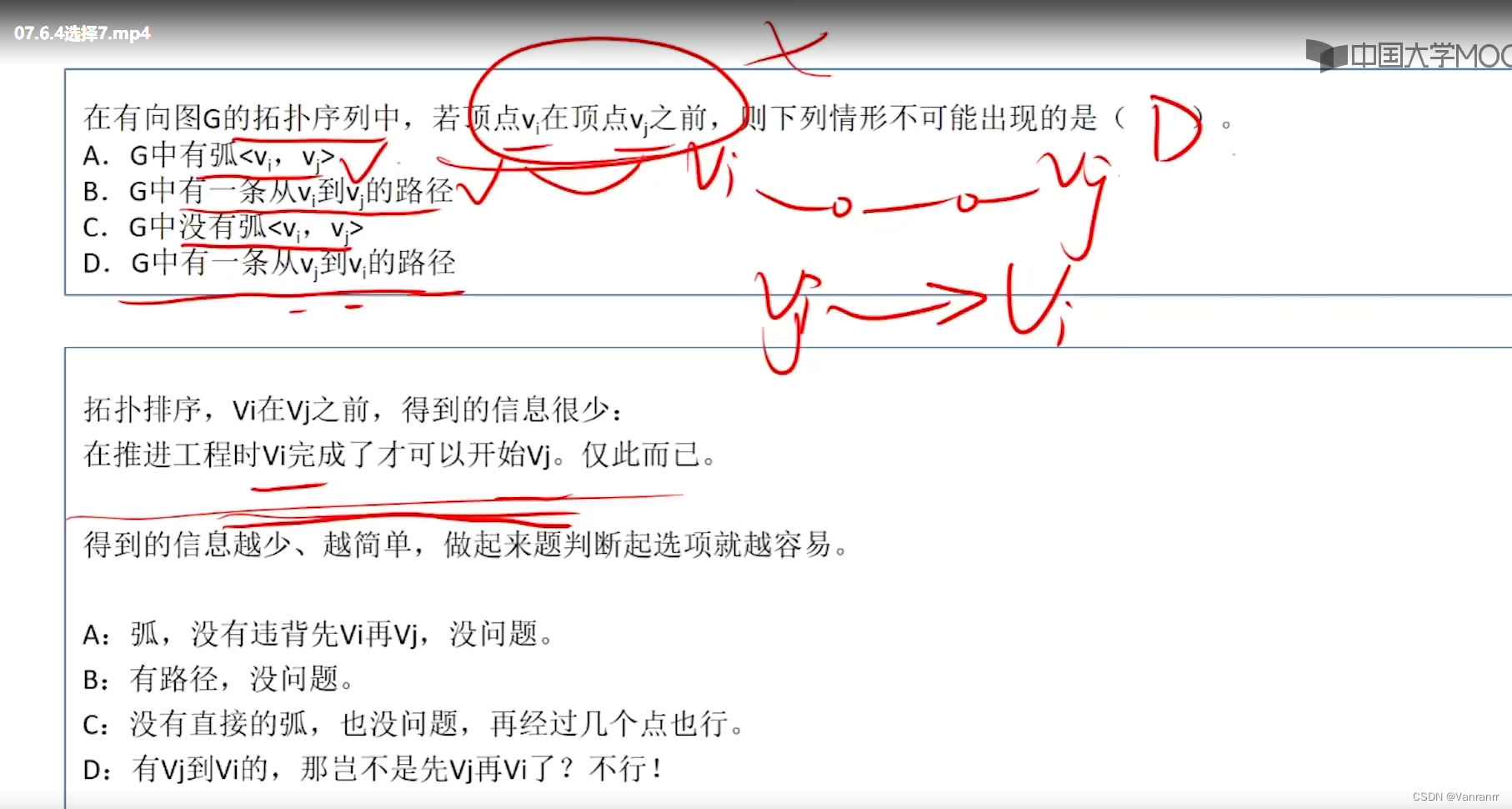
7.D
Vj完成后才能Vi 违反题意

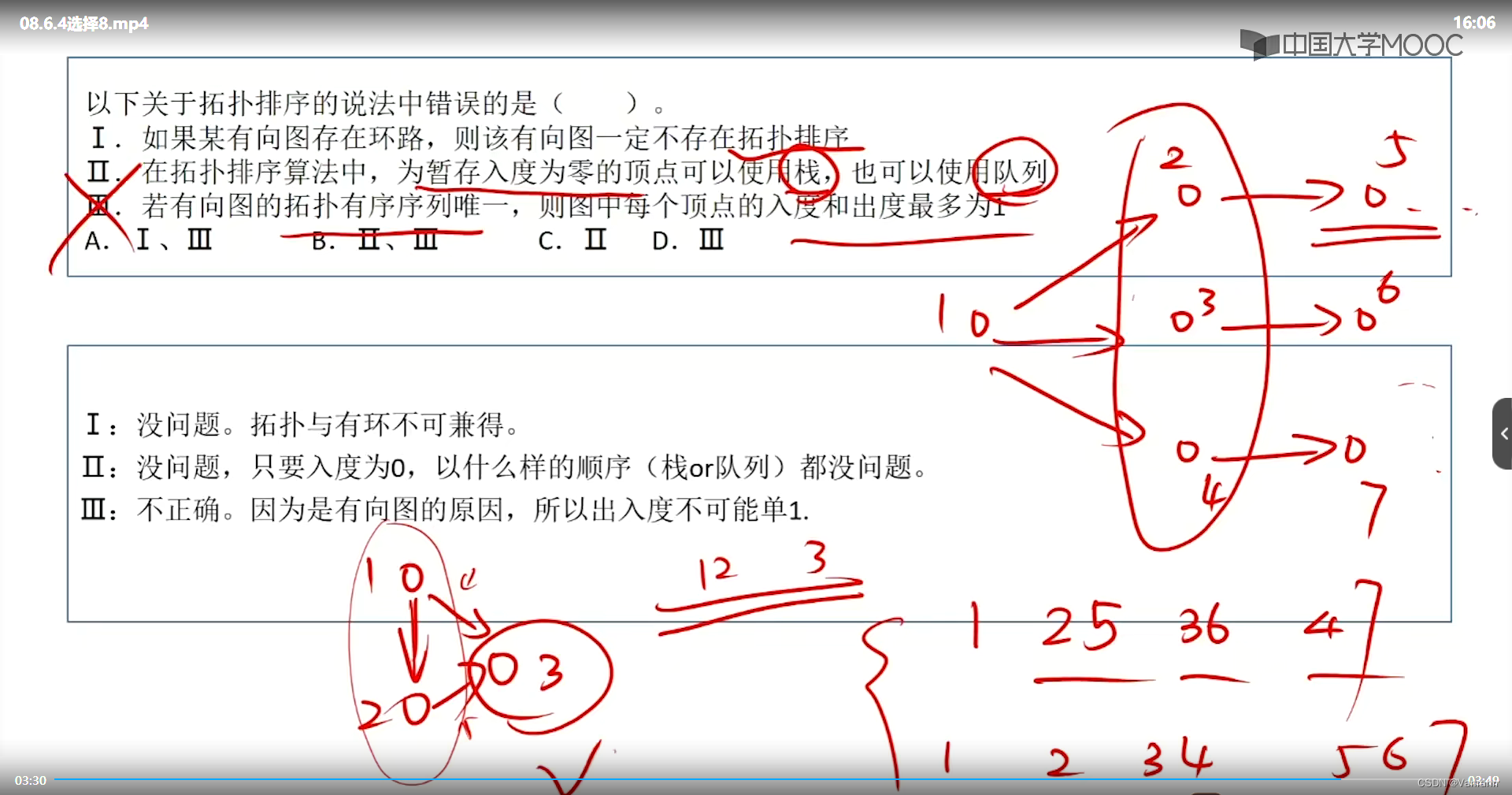
8.D

入度为0，现在可以访问了，用队列和用栈都可以
拓扑序列 用栈：1 2 5 3 6 4 7 先进先出 类似深搜
队列： 1 2 3 4 5 6 7 类似广搜
区别在这

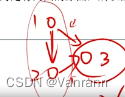
III 的反例: 3的 入度是2，拓扑有序且唯一

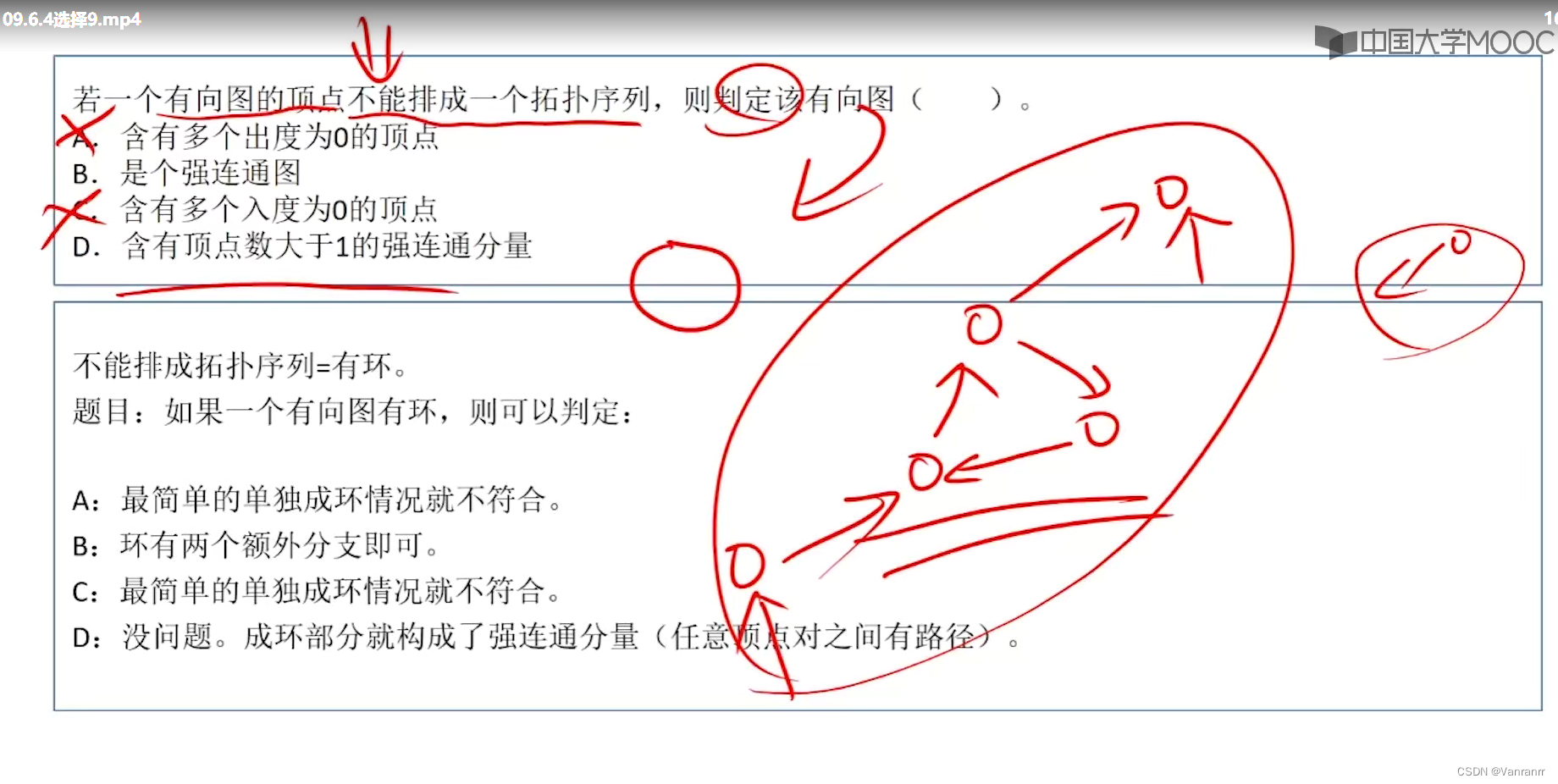
9.D中间那个环挖出来 那个环是强连通分量 顶点数>1

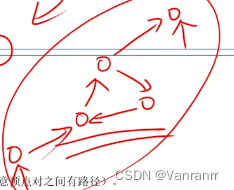
A C的反例

B的反例
最右上的顶点无法到达最左下的顶点
强连通图：任意两个顶点都有路径
强连通分量：有向图中的极大（极大指包含的顶点边最多的情况吗？）连通子图称为有向图的强连通分量
有向完全图：任意两个顶点之间都存在方向相反的两条弧

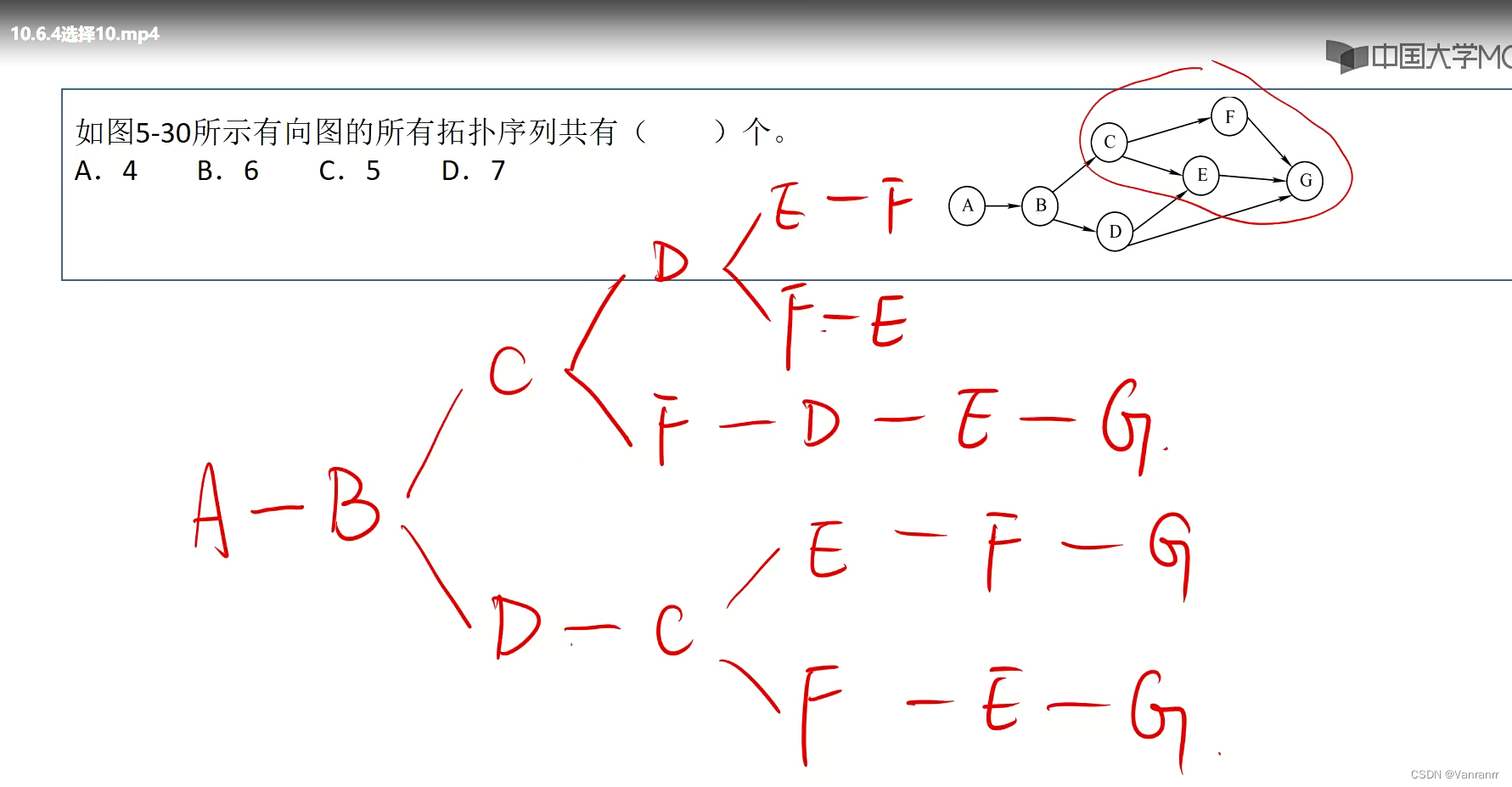
10.C
被我理解错了

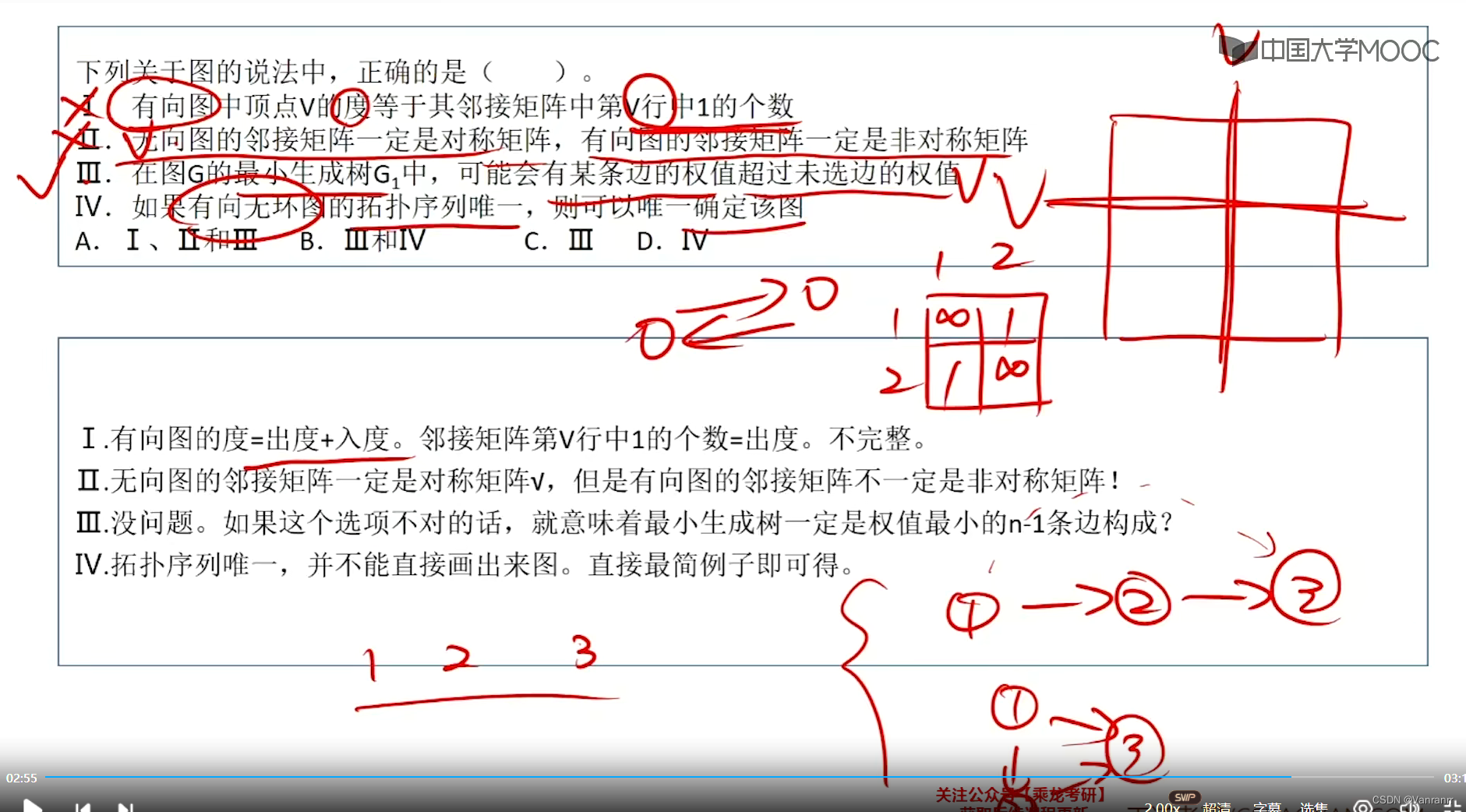
11.C
有序 编号从小到大或者编号从大到小 从小到大 行小列大 在上三角

I 行是出度
IV 拓扑序列相同且唯一 但图不止一个

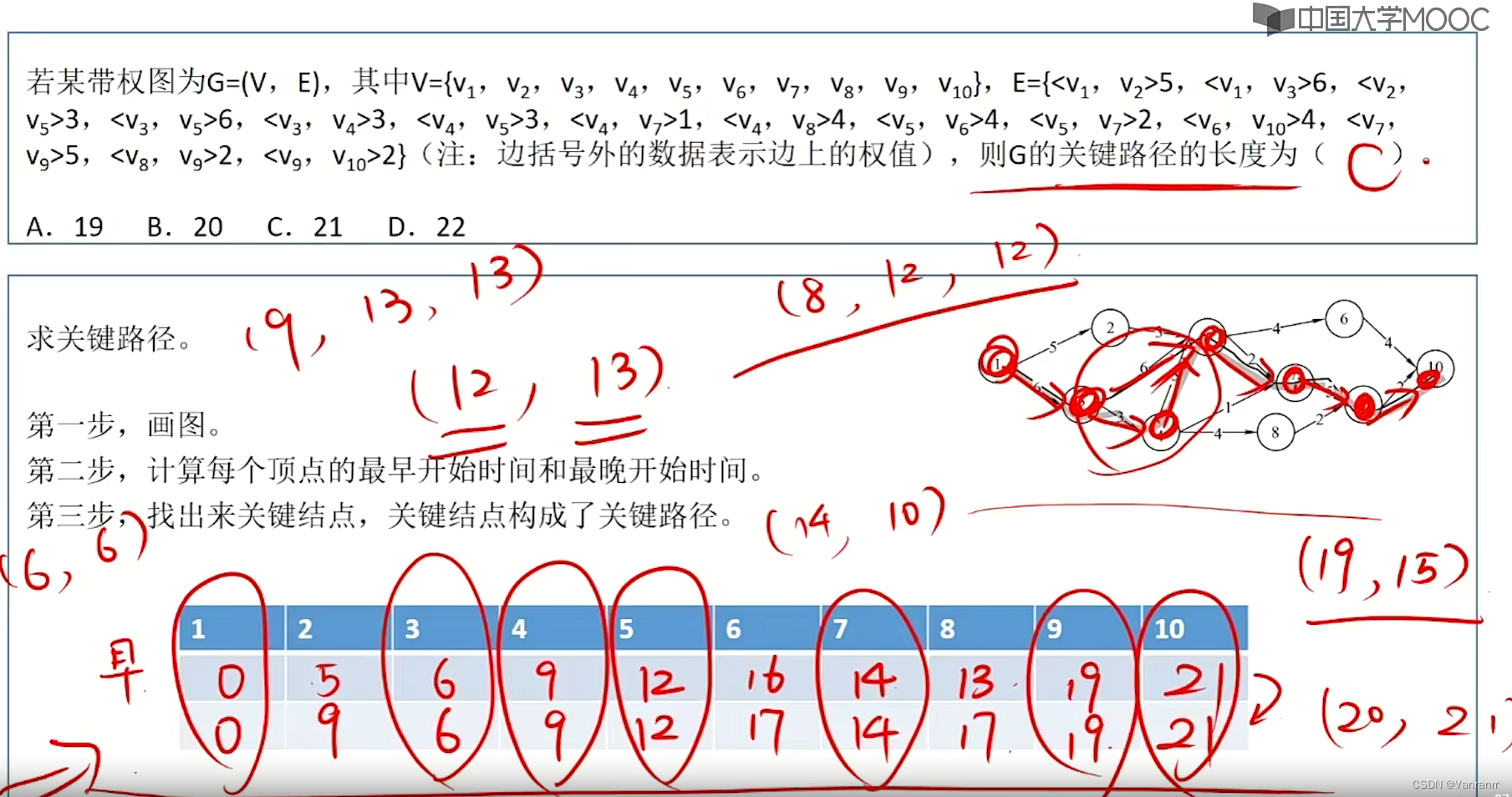
早：5号前面有三条路 三条路都完成后 五号才能开始 max(8,12,12)
晚：要取最小的min 才不会耽误