归并排序

以升序为例

文章目录

归并排序
- 基本思想
- 核心步骤
- 递归写法
- - 实现代码
- 非递归
- - 处理边界情况
  - 实现代码
- 时间复杂度

基本思想

归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用分治法的一个非常典型的应用：将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。
如果对两个有序序列的归并操作还不太熟悉，建议先看看合并两个有序链表

核心步骤

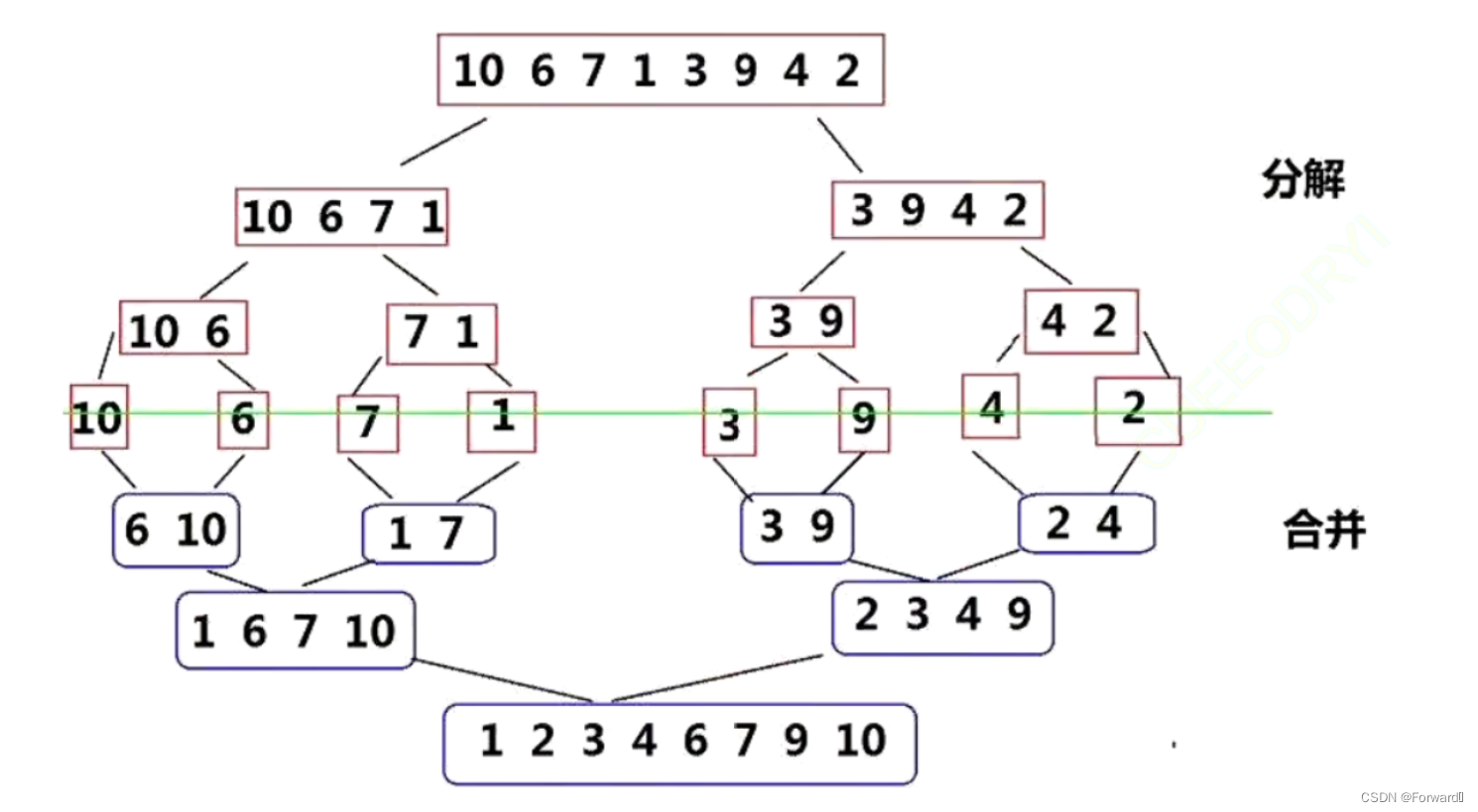
在这里插入图片描述

由上图我们可以看到，归并排序首先要对待排序列不断二分，直到分成不可分割的子序列（即只有一个元素的序列，相当于有序）
然后，再对有序的子序列不断进行归并操作，最后得到完全有序的序列。
归并排序有递归和非递归两种写法，接下来我们来讨论如何实现的具体细节：

递归写法

首先我们要注意，在进行归并操作时，为了防止原序列的元素被覆盖而导致排序错误，我们需要向内存申请一块空间用来临时存放合并的序列，同时，由于归并的此时不止一次，为防止多次申请内存而导致效率不高，我们直接向内存申请一块和原序列大小相等的空间。

void MergeSort(int *nums, int numsSize)
{
	int* temp = (int*)malloc(sizeof(int) * numsSize);
	…………;
	free(temp);                           
}

同时，归并排序在进行归并操作时需要知道每个子序列的区间，由于递归参数的限制，我们需要再定义一个子函数MergeSort()，并对这个子函数递归

void _MergeSort(int *nums, int *temp, int left, int right)
{
    …………;
}

void MergeSort(int *nums, int numsSize)
{
	int* temp = (int*)malloc(sizeof(int) * numsSize);
	_MergeSort(nums, temp, 0, numsSize - 1);
	free(temp);                           
}

易知，当子序列长度为1时，就可以不再进行二分

void _MergeSort(int *nums, int *temp, int left, int right)
{
	if (left >= right)
		return;
	…………;
}

对待排序列的左半部分和右半部分不断递归分割

void _MergeSort(int *nums, int *temp, int left, int right)
{
	if (left >= right)
		return;

	int mid = (right - left) / 2 + left;
	_MergeSort(nums, temp, left, mid);
	_MergeSort(nums, temp, mid + 1, right);

    ……………;
}

接下来，就是对两个有序序列的合并操作
注：可以走到合并这一步说明待合并的两个序列[left,mid]和[mid + 1,right]是有序的，存在两种情况：
- 情况一：例如序列{9,2}，进入函数_MergeSort()后，其子序列是单个数字，满足left >= right的条件，直接退出递归，开始合并。
- 情况二：例如序列{9,2,5,4}，进入函数_MergeSort()后，子序列{9,2}递归，合并后退出递归，然后子序列{5,4}递归，合并，退出递归，最后就变成了两个有序序列{2,9}和{4,5}的合并
- 建议对递归不是很清楚的小伙伴可以尝试画画递归展开图，这对了解递归逻辑大有裨益。

void _MergeSort(int *nums, int *temp, int left, int right)
{
	if (left >= right)
		return;

    //递归分割
	int mid = (right - left) / 2 + left;
	_MergeSort(nums, temp, left, mid);
	_MergeSort(nums, temp, mid + 1, right);

	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int index = left;

    //归并
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (nums[begin1] > nums[begin2])
			temp[index++] = nums[begin2++];
		else
			temp[index++] = nums[begin1++];
	}
	while (begin1 <= end1)
		temp[index++] = nums[begin1++];
	while (begin2 <= end2)
		temp[index++] = nums[begin2++];

    //将temp暂时存储的数据覆盖待排序列nums原有位置的数据，实现待排序列区间有序
	for (int i = left; i <= right; i++)
		nums[i] = temp[i];
}

实现代码

void _MergeSort(int *nums, int *temp, int left, int right)
{
	if (left >= right)
		return;

    //递归分割
	int mid = (right - left) / 2 + left;
	_MergeSort(nums, temp, left, mid);
	_MergeSort(nums, temp, mid + 1, right);

	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int index = left;

    //归并
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (nums[begin1] > nums[begin2])
			temp[index++] = nums[begin2++];
		else
			temp[index++] = nums[begin1++];
	}
	while (begin1 <= end1)
		temp[index++] = nums[begin1++];
	while (begin2 <= end2)
		temp[index++] = nums[begin2++];

    //将temp暂时存储的数据覆盖待排序列nums原有位置的数据（拷贝回去），实现待排序列区间有序
	for (int i = left; i <= right; i++)
		nums[i] = temp[i];
}

void MergeSort(int *nums, int numsSize)
{
	int* temp = (int*)malloc(sizeof(int) * numsSize);
	_MergeSort(nums, temp, 0, numsSize - 1);
	free(temp);                           
}

非递归

我们可以直接用循环解决问题，如图所示：

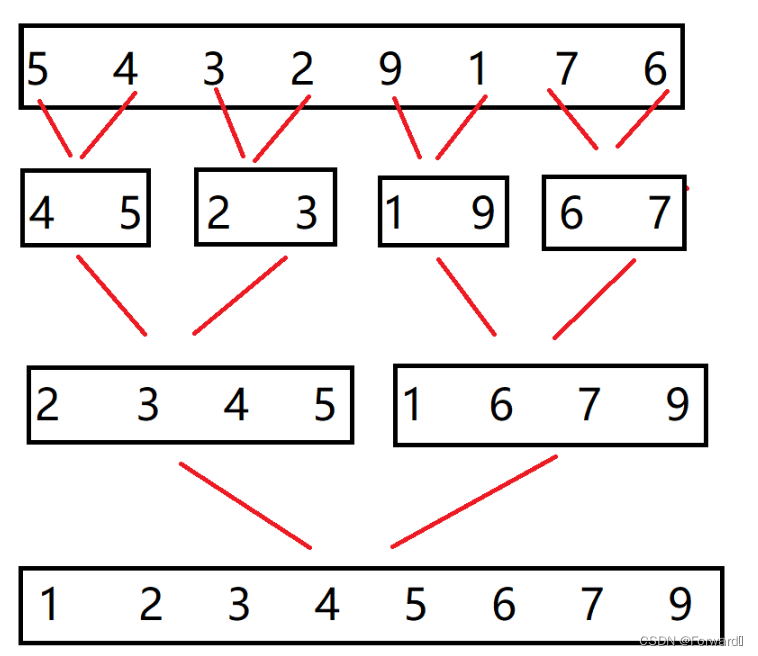
在这里插入图片描述

由上面的递归分析可以知道，两个单个数字可以直接合并成一个有序序列。因此我们定义gap，表示每次合并的两个序列长度为gap，gap从1递增，直到不能满足条件gap < numsSize，然后就进行和递归相同的合并操作就可以了

void MergeSort(int* nums, int numsSize)
{
	int* temp = (int*)malloc(sizeof(int) * numsSize);

	int gap = 1;

	while (gap < numsSize)
	{
        /*
        	因为每次是对两个有序序列进行合并
        	因此每次合并过后i应该跳过两个序列长度
        */
		for (int i = 0; i < numsSize; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			int index = begin1;
			
            //归并
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (nums[begin1] < nums[begin2])
					temp[index++] = nums[begin1++];
				else
					temp[index++] = nums[begin2++];
			}
			while(begin1 <= end1)
				temp[index++] = nums[begin1++];
			while(begin2 <= end2)
				temp[index++] = nums[begin2++];
			
            //将temp暂时存储的数据覆盖待排序列nums原有位置的数据（拷贝回去），实现待排序列区间有序
			for (int j = i; j <= end2; j++)
				nums[j] = temp[j];
		}

		gap *= 2;
	}

	free(temp);
}

处理边界情况

看起来好像很简单，但上面的代码仍存在些许bug，仍需要我们谨慎处理
我们来看一个情况，如果给的待排数组是{5,4,3,2,9,7,1,6,8}

在这里插入图片描述

如果给的待排数组是{5,4,3,2,9,7

在这里插入图片描述

int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int index = begin1;

/*
	如果右半区间不存在，只有左半区间
	说明待合并的只有一个区间
	显然没有合并的必要，直接退出合并循环即可
*/
if (begin2 >= numsSize)
    break;

//如果右半区间算多了，那么对end2进行修正
if (end2 >= numsSize)
    end2 = numsSize - 1;

实现代码

void MergeSort(int* nums, int numsSize)
{
	int* temp = (int*)malloc(sizeof(int) * numsSize);

	int gap = 1;

	while (gap < numsSize)
	{
        /*
        	因为每次是对两个有序序列进行合并
        	因此每次合并过后i应该跳过两个序列长度
        */
		for (int i = 0; i < numsSize; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
            int begin2 = i + gap, end2 = i + 2 * gap - 1;
            int index = begin1;

            /*
                如果右半区间不存在，只有左半区间
                说明待合并的只有一个区间
                显然没有合并的必要，直接退出合并循环即可
            */
            if (begin2 >= numsSize)
                break;

            //如果右半区间算多了，那么对end2进行修正
            if (end2 >= numsSize)
                end2 = numsSize - 1;
            
            
			 //归并
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (nums[begin1] < nums[begin2])
					temp[index++] = nums[begin1++];
				else
					temp[index++] = nums[begin2++];
			}
			while(begin1 <= end1)
				temp[index++] = nums[begin1++];
			while(begin2 <= end2)
				temp[index++] = nums[begin2++];
			
            //将temp暂时存储的数据覆盖待排序列nums原有位置的数据（拷贝回去），实现待排序列区间有序
			for (int j = i; j <= end2; j++)
				nums[j] = temp[j];
		}

		gap *= 2;
	}

	free(temp);
}