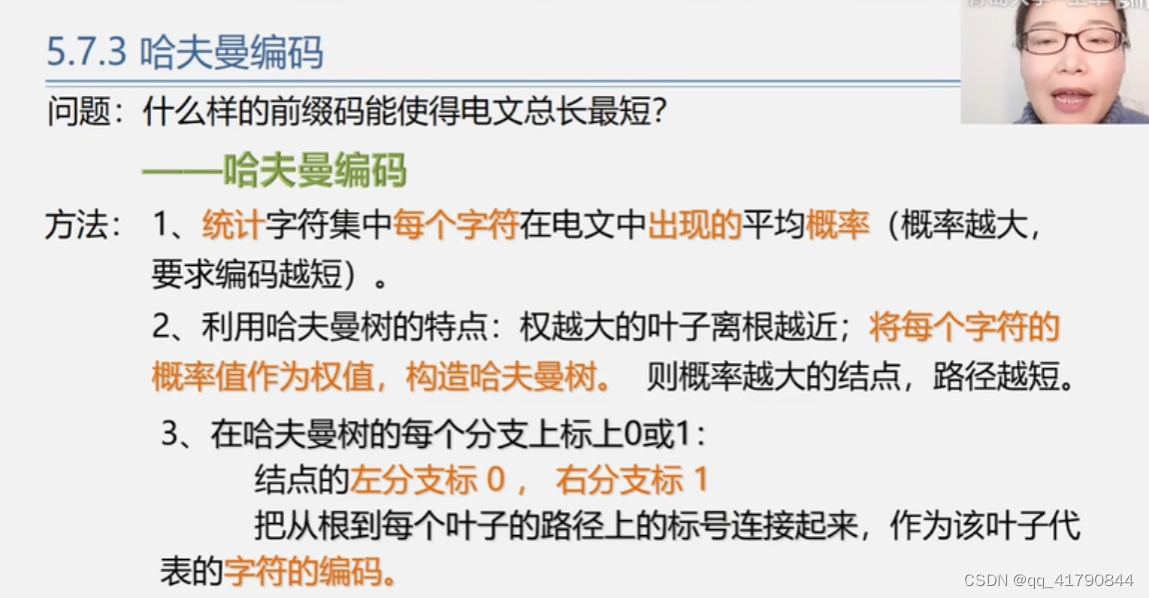
构造n个给定值节点构成的森林;
选择权值最小的两个构成叶子节点,根节点权值为两叶子节点之和,
删除原有的两棵树,将这棵树加入森林中;
重复这两部直到只有一棵树为止,此树就是哈夫曼树;
#pragma once
#include<iostream>
namespace stlname
{
using std::cin;
typedef struct
{
int weight;//权重
int parent, lch, rch; //父节点,孩子节点下标
}HTNode,*HuffmanTree;
void Seclect(HuffmanTree HT,int i ,int* s1,int* s2);
void CreateHuffmanTree(HuffmanTree HT, int n)//初始化
{
if (n <= 1)return;
int m = 2 * n - 1;
HT = new HTNode[m+1]();//2n个节点;
for (int i = 1; i < m + 1; i++)
{
HT[i].lch = HT[i].rch = HT[i].parent = 0;//初始化
}
for (int i = 1; i <= n; i++)std::cin >> HT[i].weight;
int* s1, * s2 = NULL;
for (int i = n + 1; i < m; i++)
{
Seclect(HT, i - 1, s1, s2);
HT[*s1].parent = i; HT[*s2].parent = i;
HT[i].lch = *s1; HT[i].rch = *s2;
HT[i].weight = HT[*s1].weight + HT[*s2].weight;
}
}
}
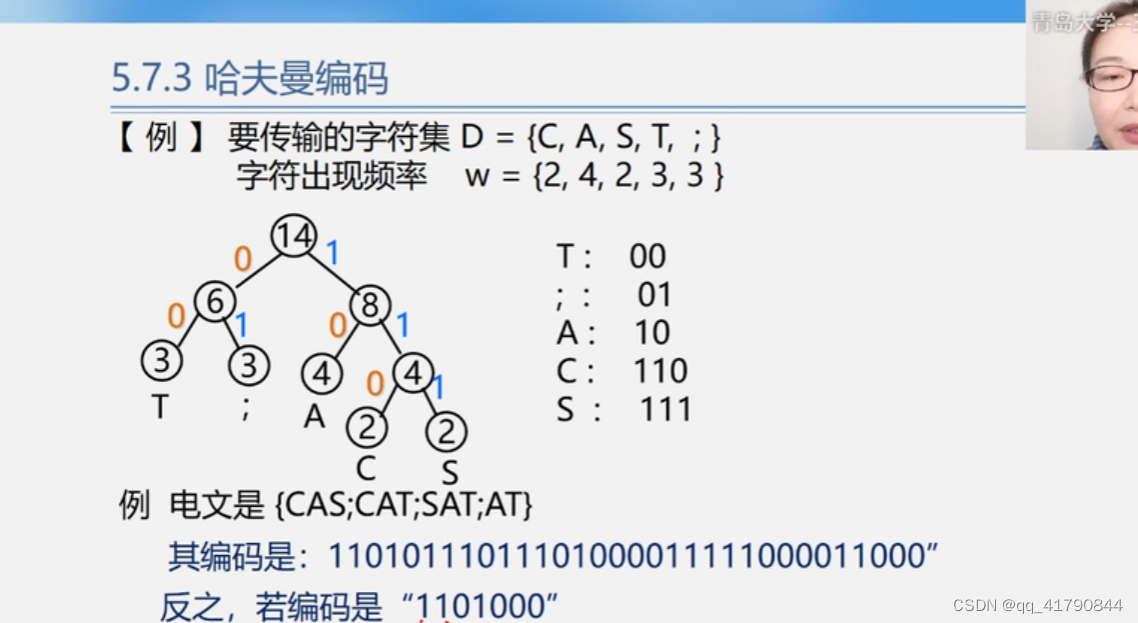
哈夫曼编码算法实现:
void CreateHuffmanCode(HuffmanTree HT, HuffmanCode HC, int n)
{
HC = new char* [n + 1];
char* cd = new char[n];
cd[n - 1] = '\0';
for (int i = 1; i < n; i++)
{
int start = n - 1; int c = i;
int f = HT[i].parent;
while (start != 0) {
start--;
if (HT[f].lch == c) { cd[start] == '0'; }
else cd[start] = '1';
c = f;
f = HT[f].parent;
}
strcpy(HC[i],&cd[start]);
}
delete cd; cd = NULL;
}