根据惠更斯 － 菲涅耳原理，光的衍射是光束内部的次波之间的相干叠加，衍射光波场的光振动符合菲涅耳积分公式。但直接运用菲涅耳积分公式计算衍射光场是很困难的。对于夫琅和费衍射(远场衍射)，在光源和接收屏距离衍射屏均为无穷远的情况下，通过较为简单的积分运算即可得到较精确的衍射光振动和光强分布。而对于菲涅耳衍射(近场衍射)，即光源和接收屏距离衍射屏至少一个为有限远，只能通过近似方法(如半波带法)半定量地得出轴上一点的衍射光强。当轴上点对应的半波带数 k = 奇数时，则该点为亮点，若半波带数 k = 偶数时，则该点为暗点。

       轴外光强分布的定量分析难度很大，目前未见系统的研究。MATLAB 软件具有强大的计算和可视化功能，可以较为精确地模拟光学实验的结果，可避开复杂的光学理论推导以及条件苛刻的光学实验测量，使复杂、抽象的光学现象变得具体、直观。

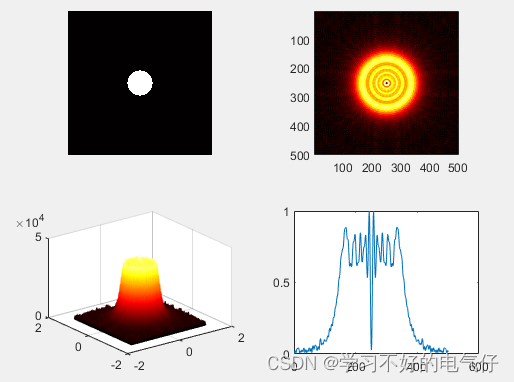
 完整代码：

clc;
clear;
close all;
warning off;
addpath(genpath(pwd));

step = 350;
lamda = 500e-6; %changed
k = 2*pi/lamda;
z = 12.5; %changed 
%确定衍射屏
N = 500; %圆屏采样点数
r = 0.25; %changed
I = zeros(N, N);
[m, n] = meshgrid(linspace(-N/step, N/step, N));
D = (m.^2+n.^2).^(1/2);
i = find(D <= r);
I(i) = 1;  %空半径范围内透射系数为1
q = exp(j*k*(m.^2+n.^2)/2/z);
subplot(2,2,1); %圆孔图像
imshow(I);
%imagesc(I) %衍射屏图像
%colormap([0 0 0;1 1 1]) %黑白区分
% 
% I = I.*q;
L = 500;
M = 500; %取相同点数用于矩阵运算
[x, y] = meshgrid(linspace(-L/step, L/step, M));
h = exp(j*k*z)*exp((j*k*(x.^2+y.^2))/(2*z))/(j*lamda*z); %接收屏
%H = fftshift(fft2(h));
B = fftshift(fft2(I.*q));
G = h.*B; %
% U = fftshift(ifft2(G));
%Br = (abs(G)/max(abs(G))); %归一化
C = abs(G);
subplot(2,2,2);imagesc(C);
axis image;
colormap(hot);
% %figure;
subplot(2,2,3);mesh(x,y,abs(G));
subplot(2,2,4);
axis image;
d = C(251,:);
d = d/max(d);
plot(d);