注：参考B站视频教程

视频链接：【(强推|双字)2022吴恩达机器学习Deeplearning.ai课程】

---

第一周

一、监督学习与无监督学习

监督学习：输入数据和标签，让机器进行学习后，再输入一个它从未见过的数据，让机器预测输出。

一些监督学习的例子：

---

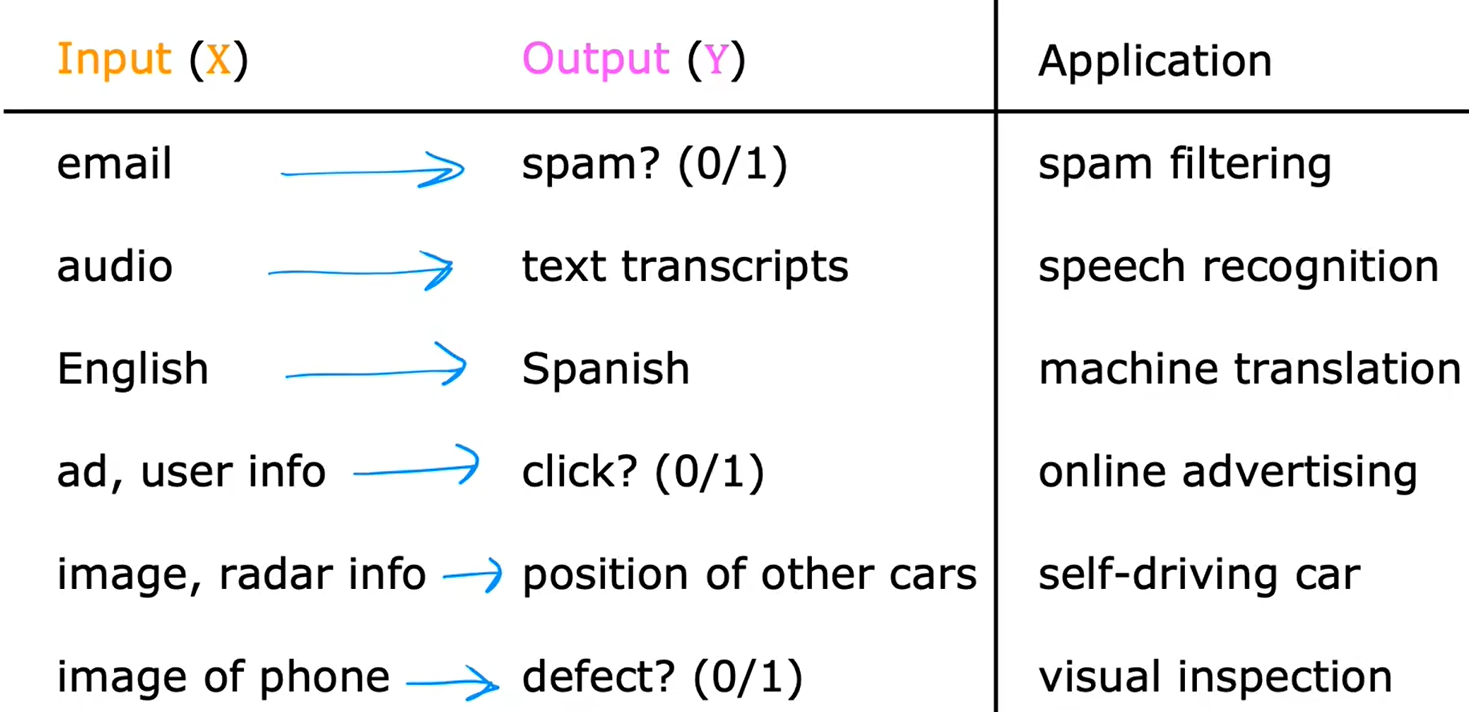
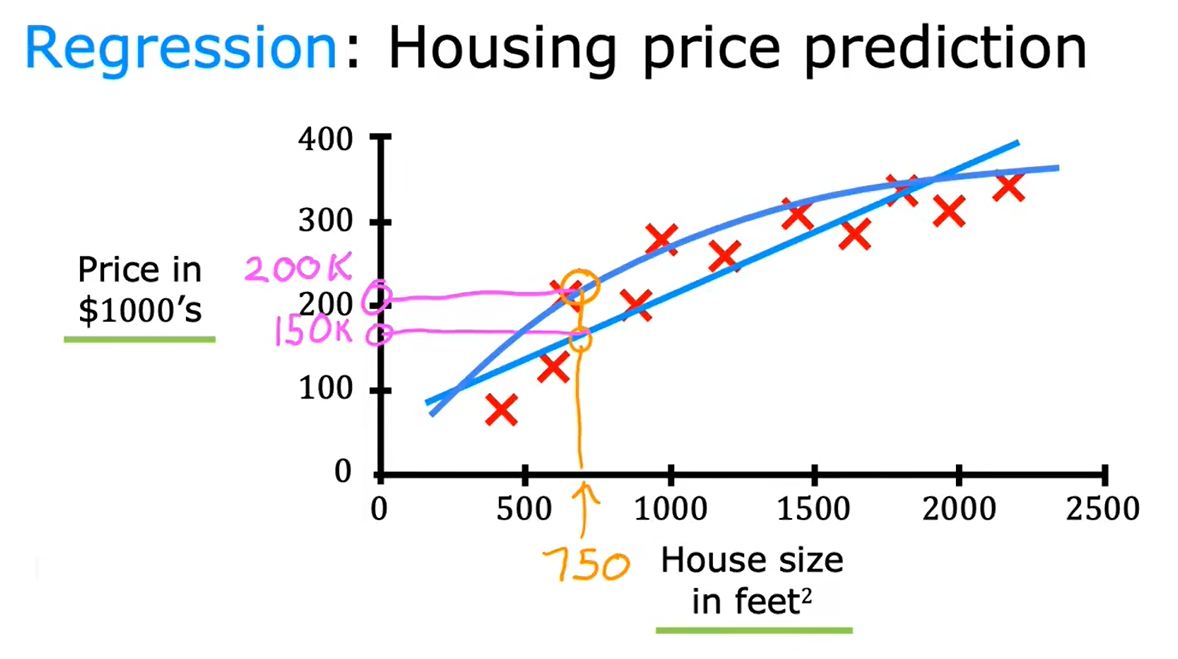
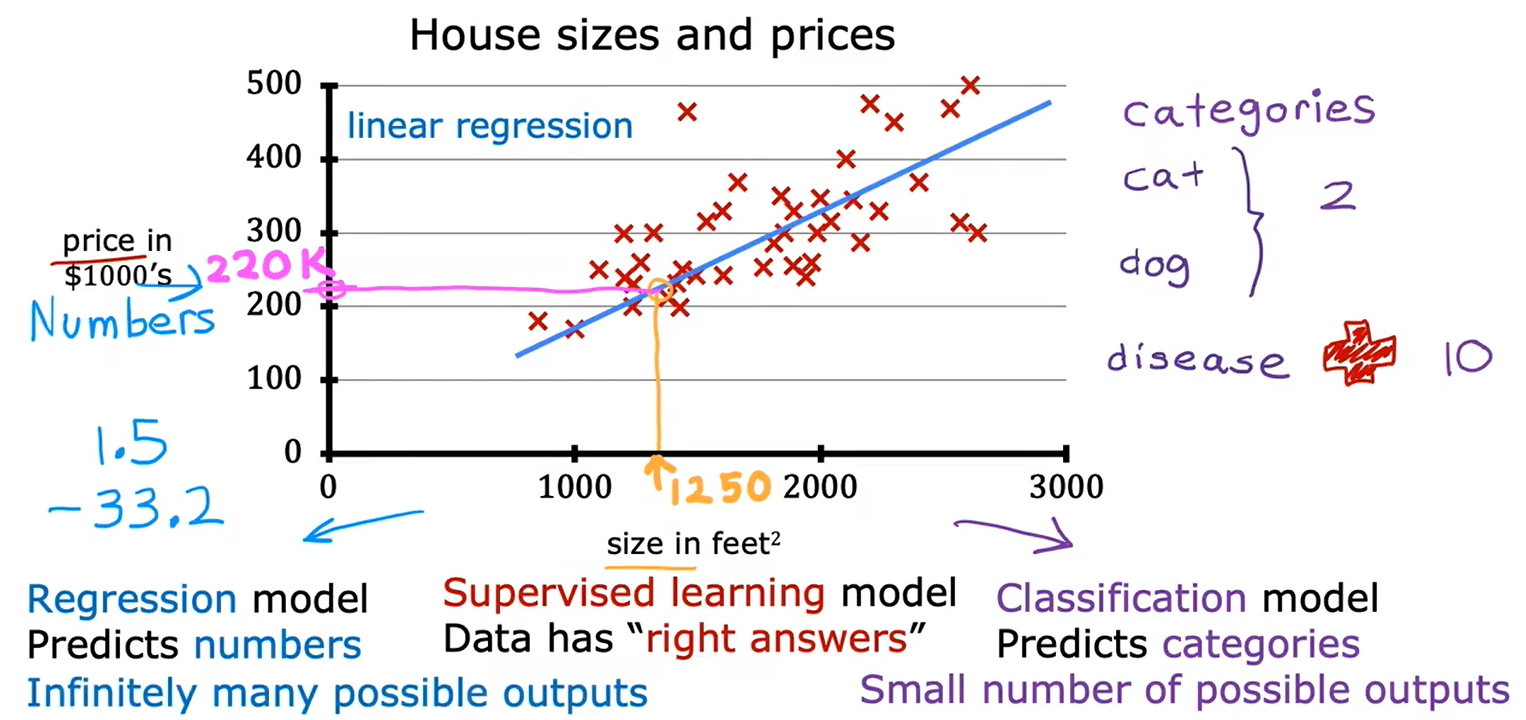
1、回归：房价预测

---

2、分类：乳腺癌检测

---

---

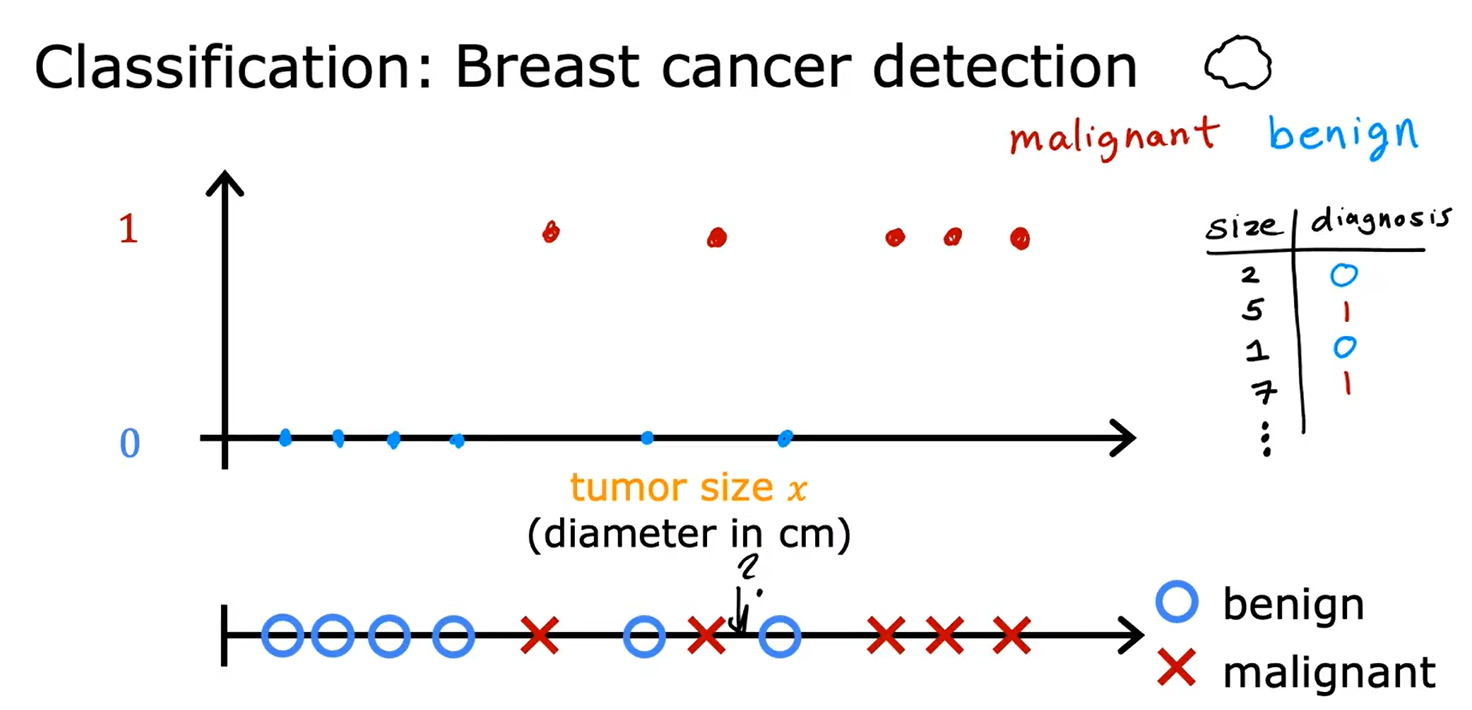
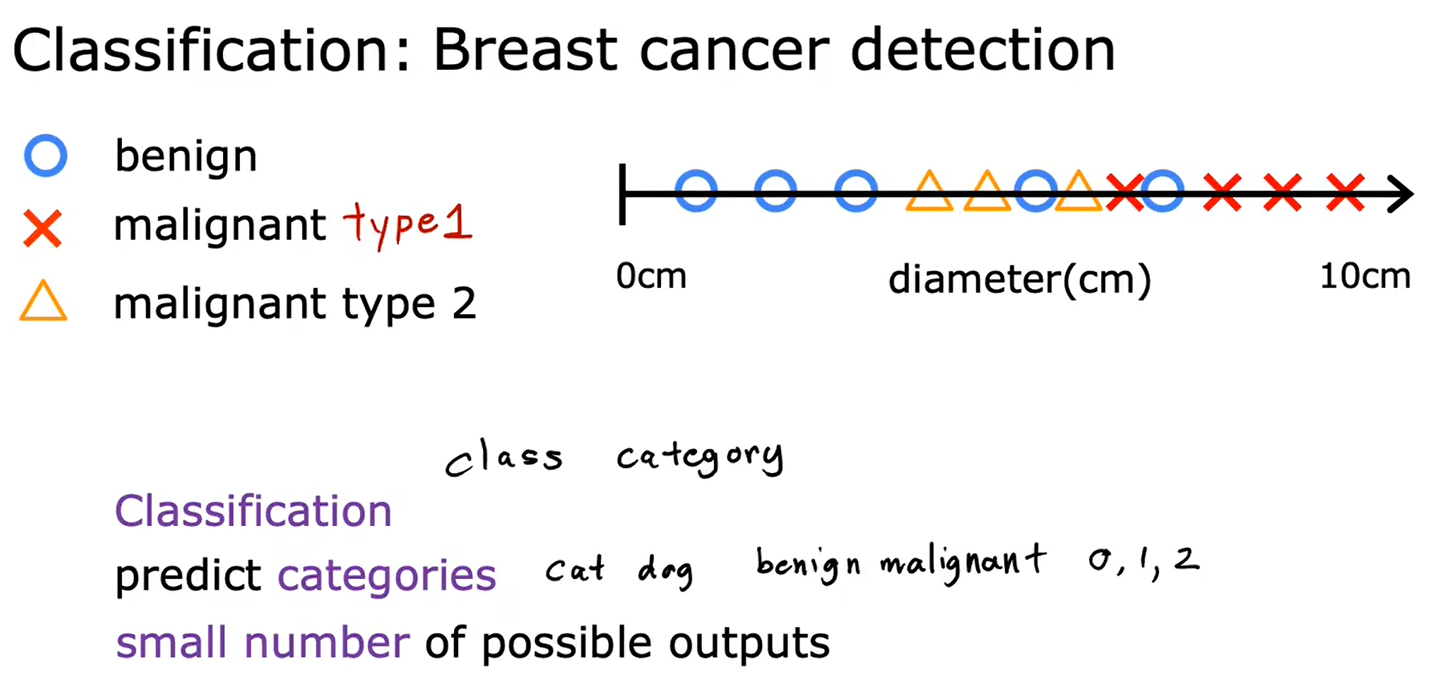
分类需要找到一个“决策边界”

---

3、监督学习总结

---

无监督学习：数据和标签之间没有联系

---

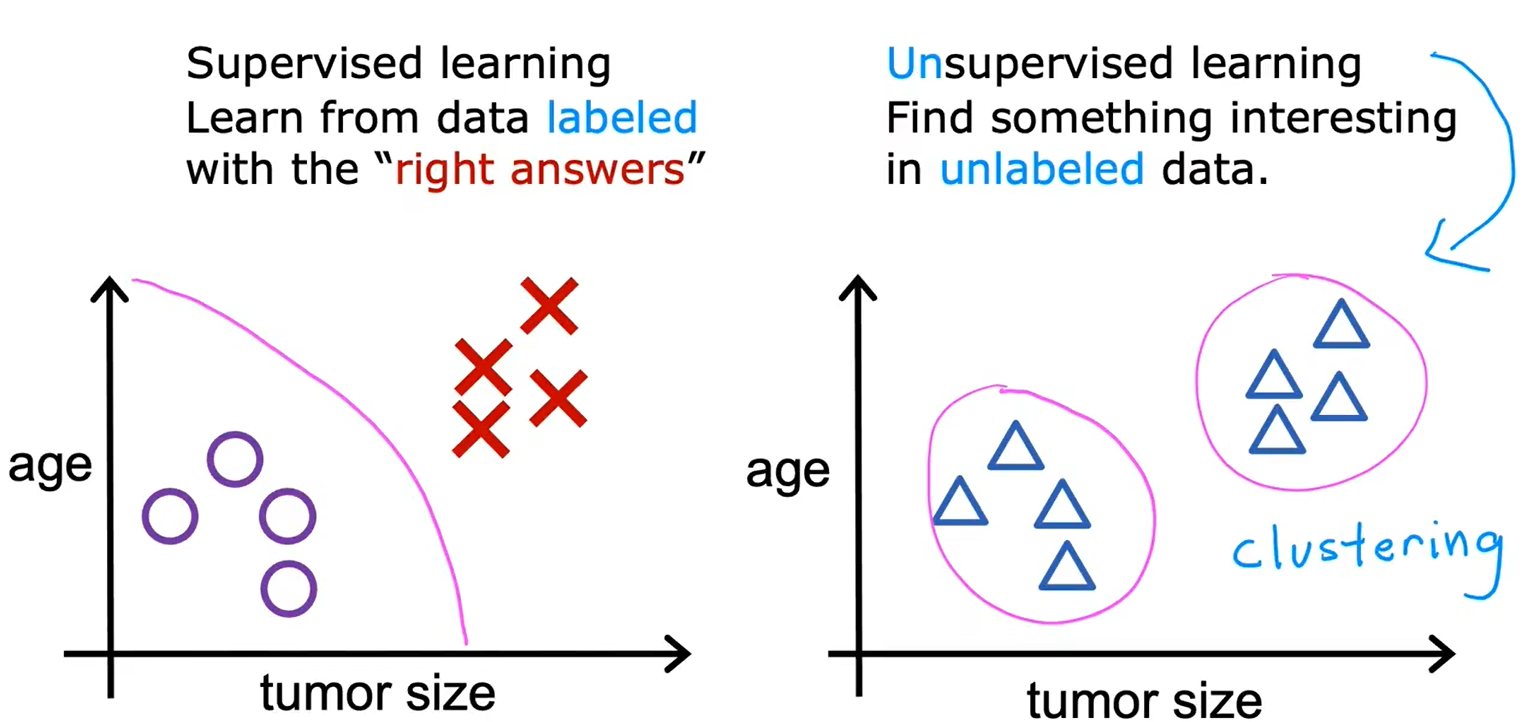
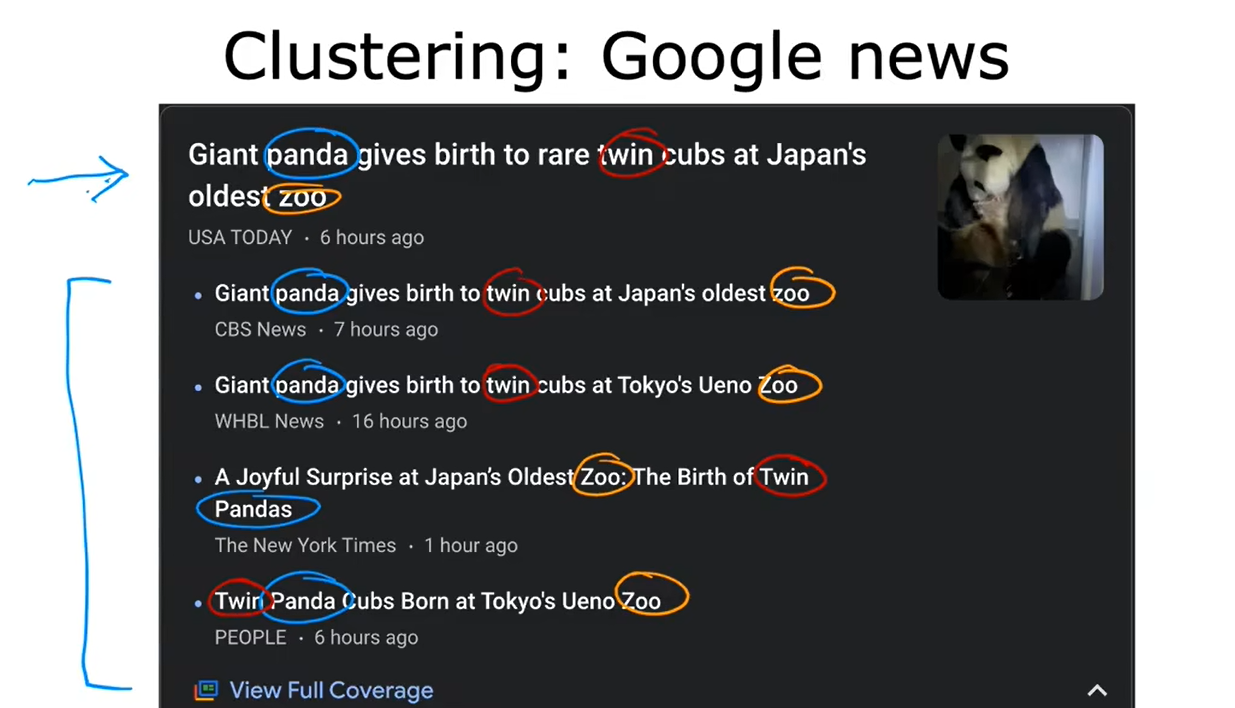
4、聚类：新闻&基因序列&人员分组
聚类：获取没有标签的数据，尝试将他们自动分组到不同的簇中去。

---

---

---

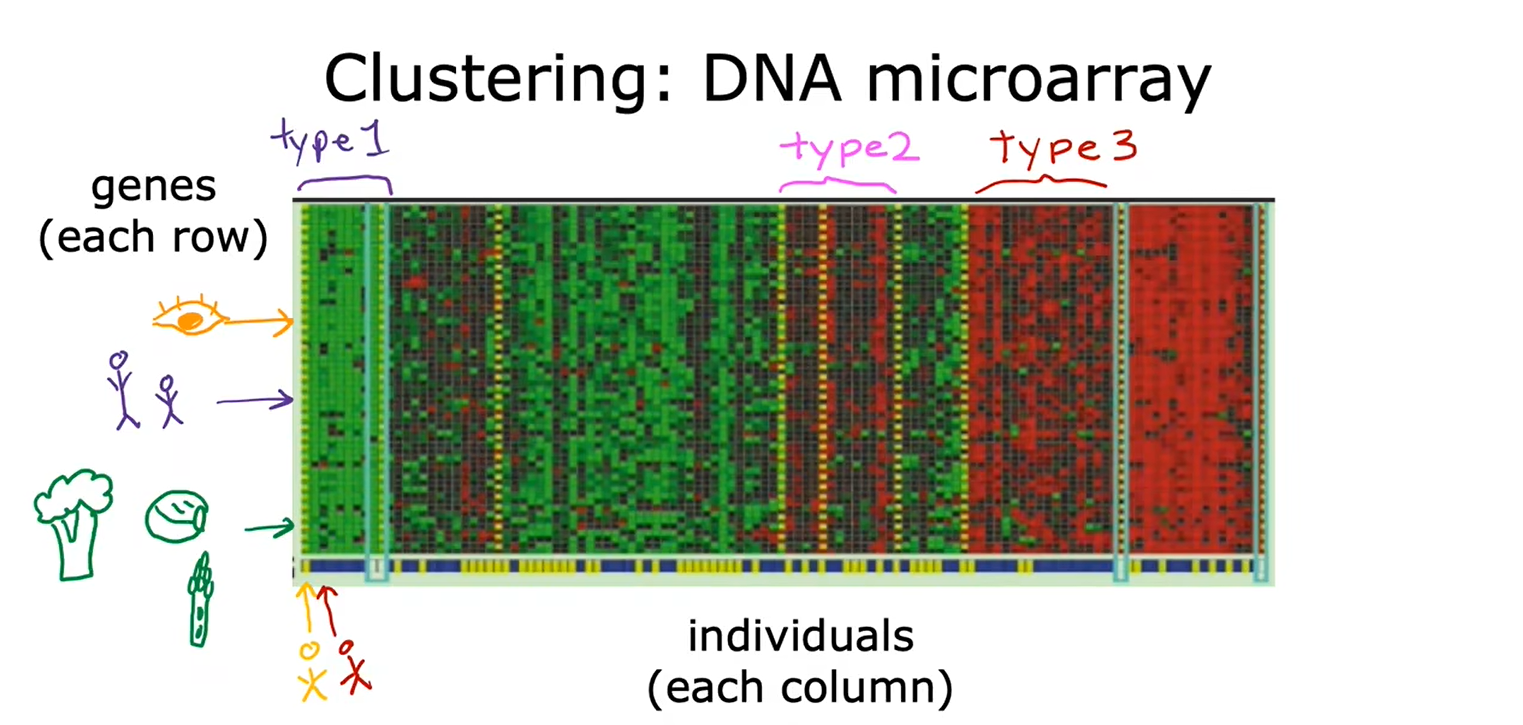
5、无监督学习的总结

---

---

二、线性回归

线性回归模型是一种特殊类型的监督学习模型

1、线性回归模型

---

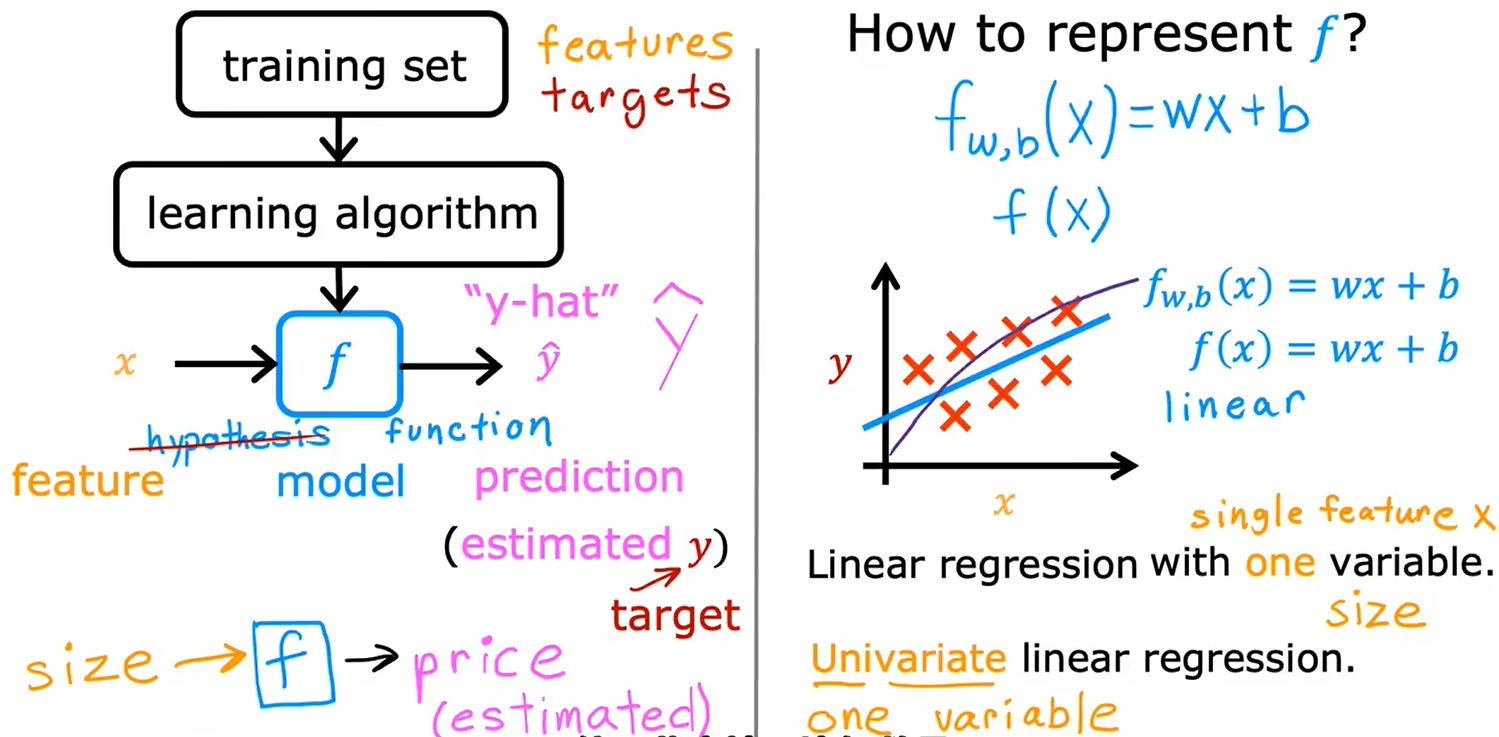
训练集：

---

预测函数 f（x）

---

2、代价函数
a、代价函数公式

---

---

---

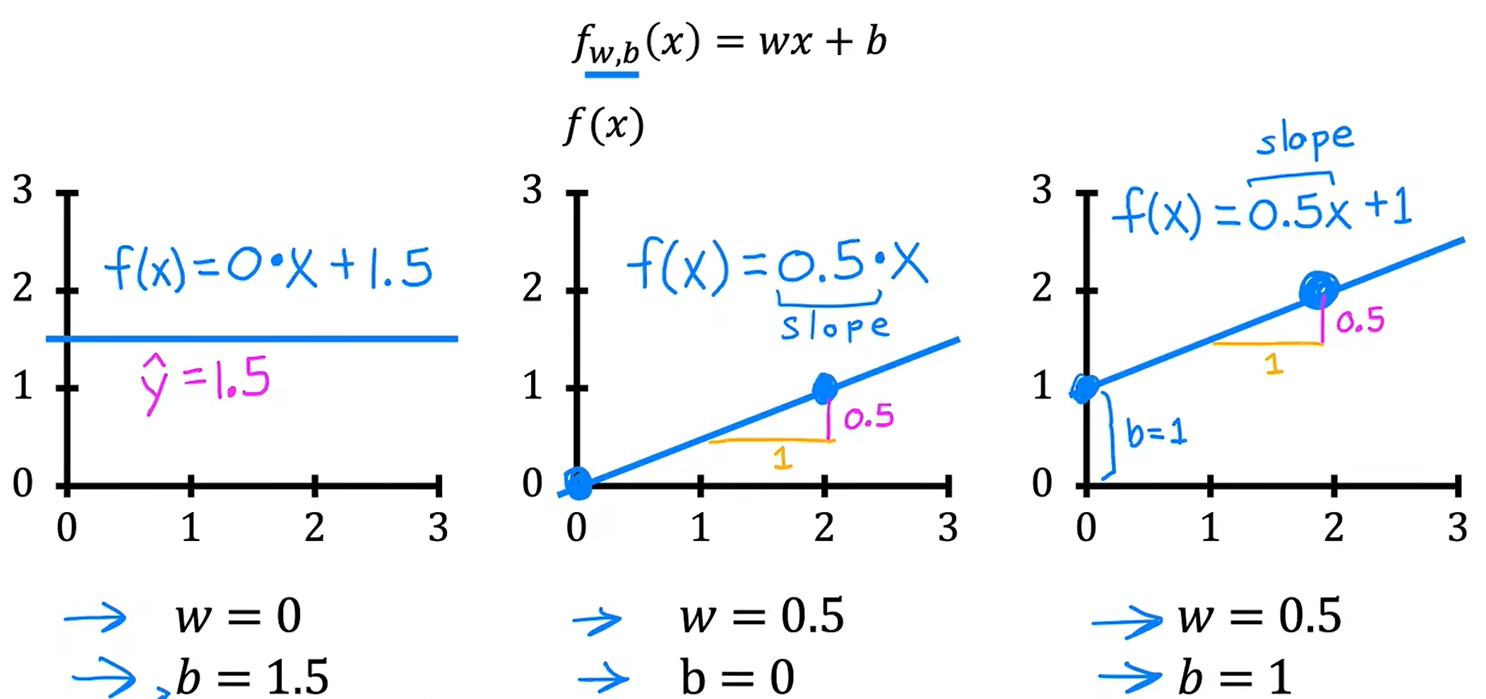
b、理解代价函数

---

---

---

---

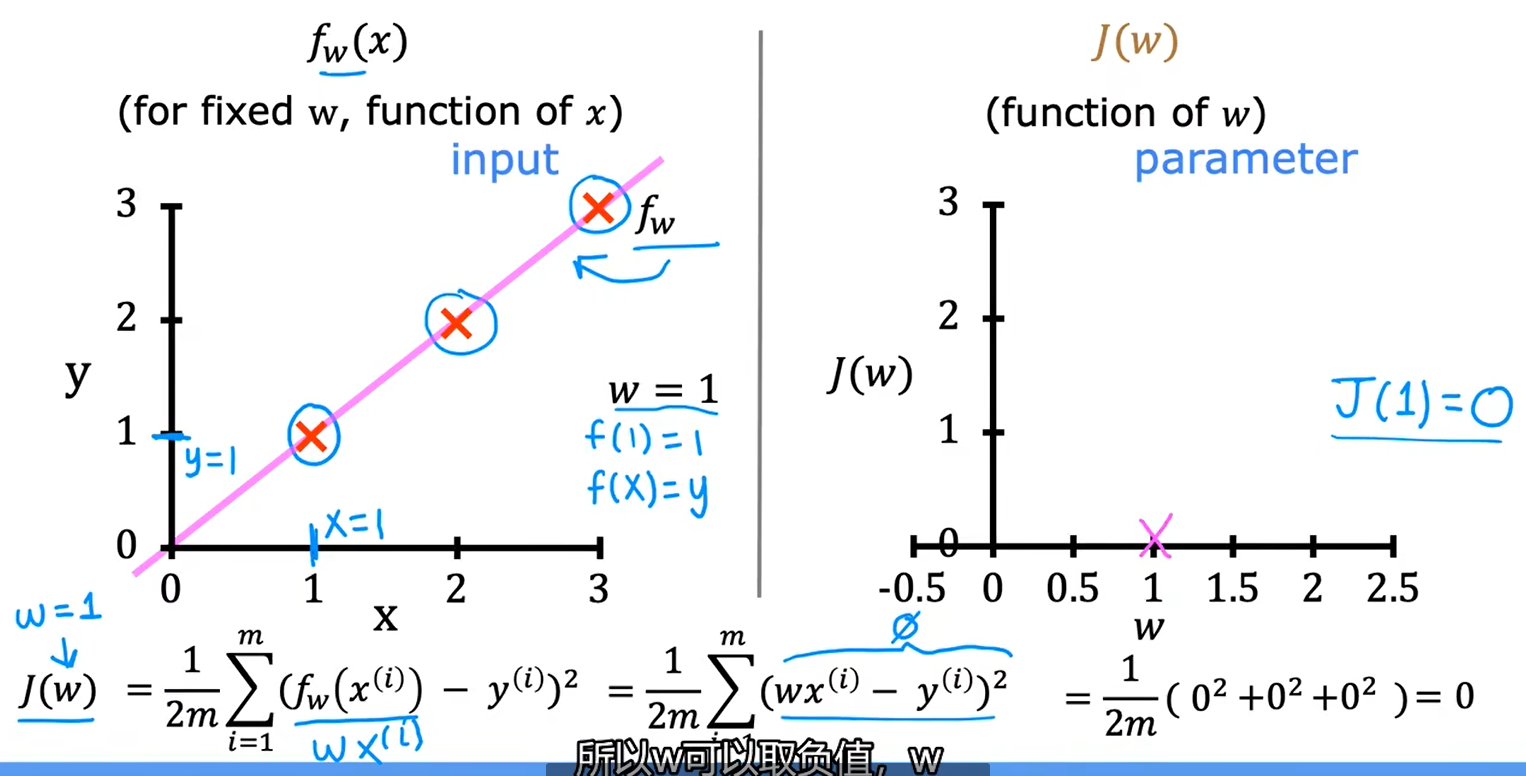
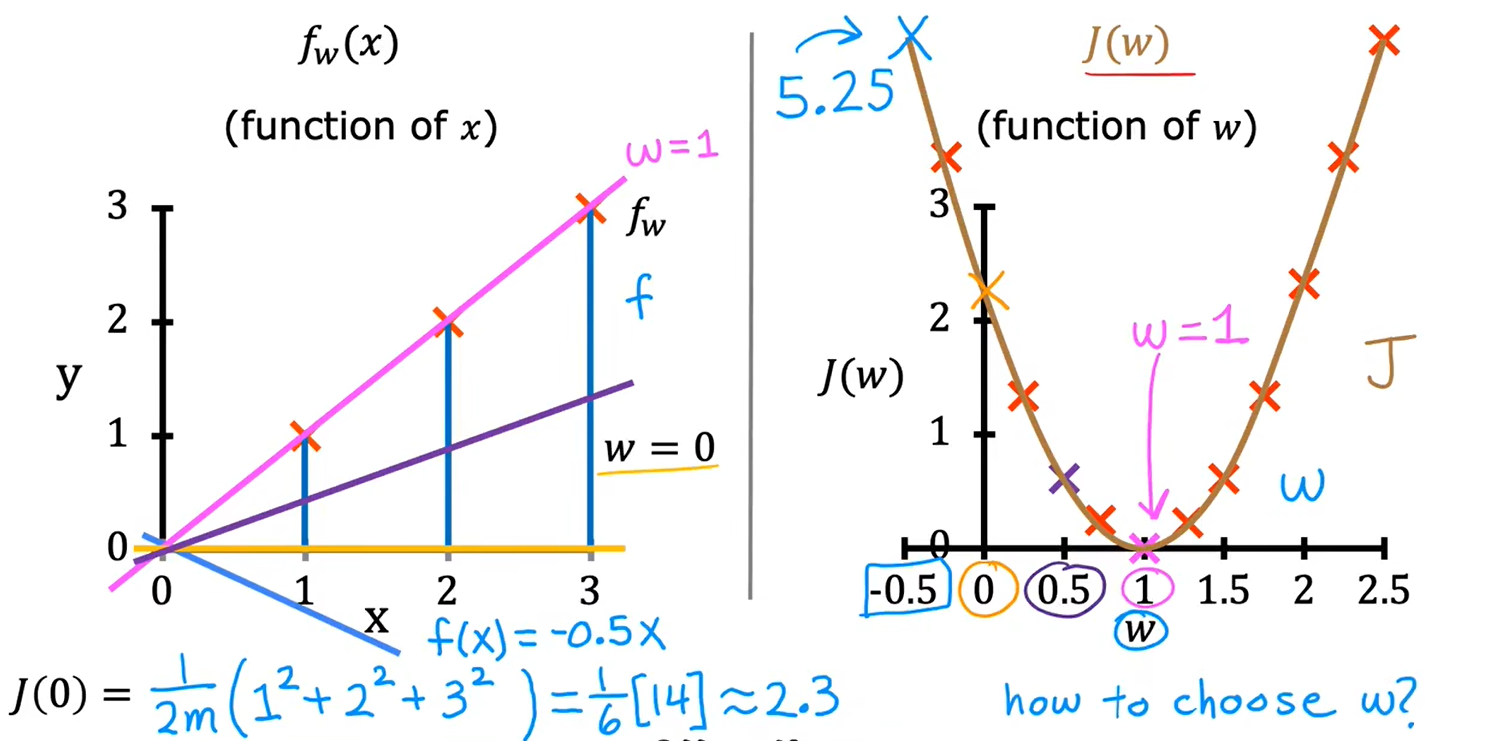
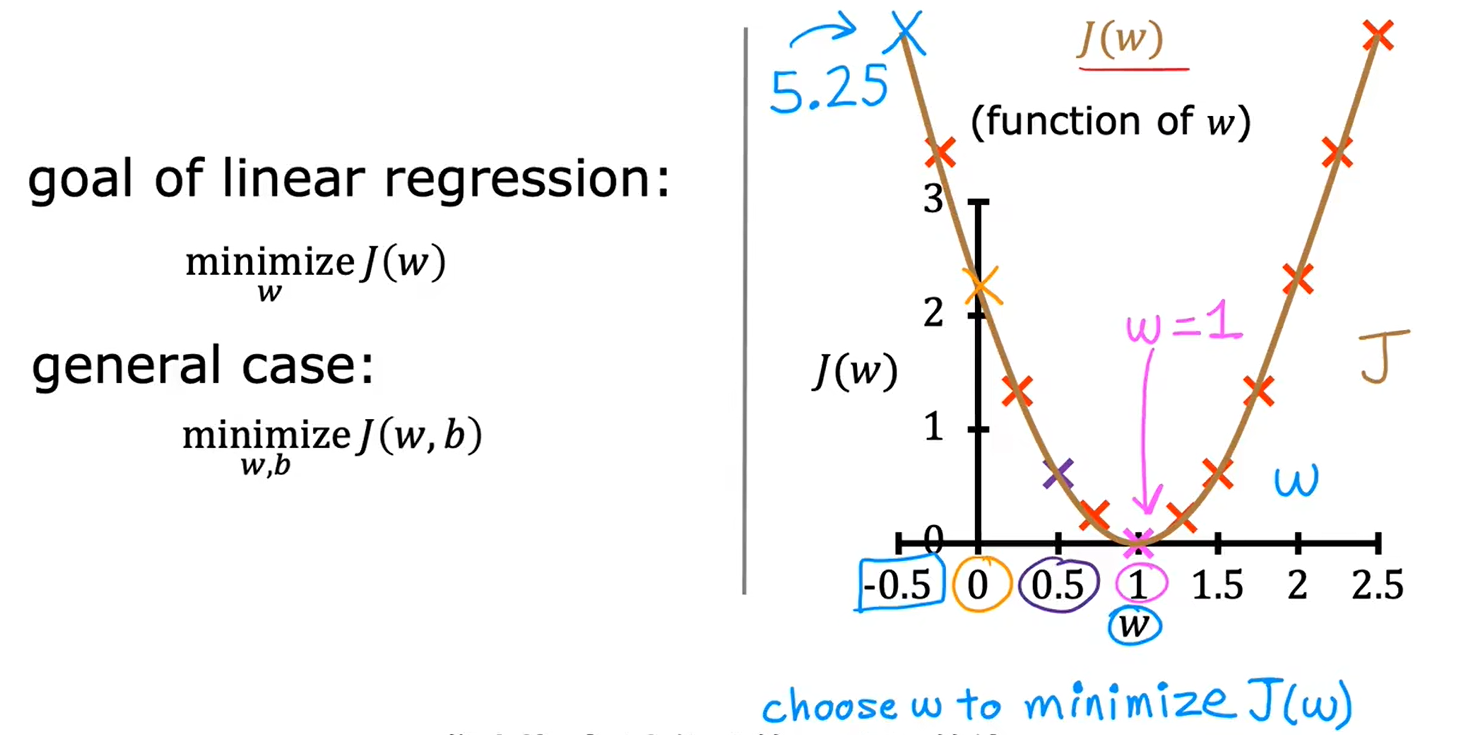
c、可视化代价函数

当只有一个参数w时，代价函数看起来像U型曲线

---

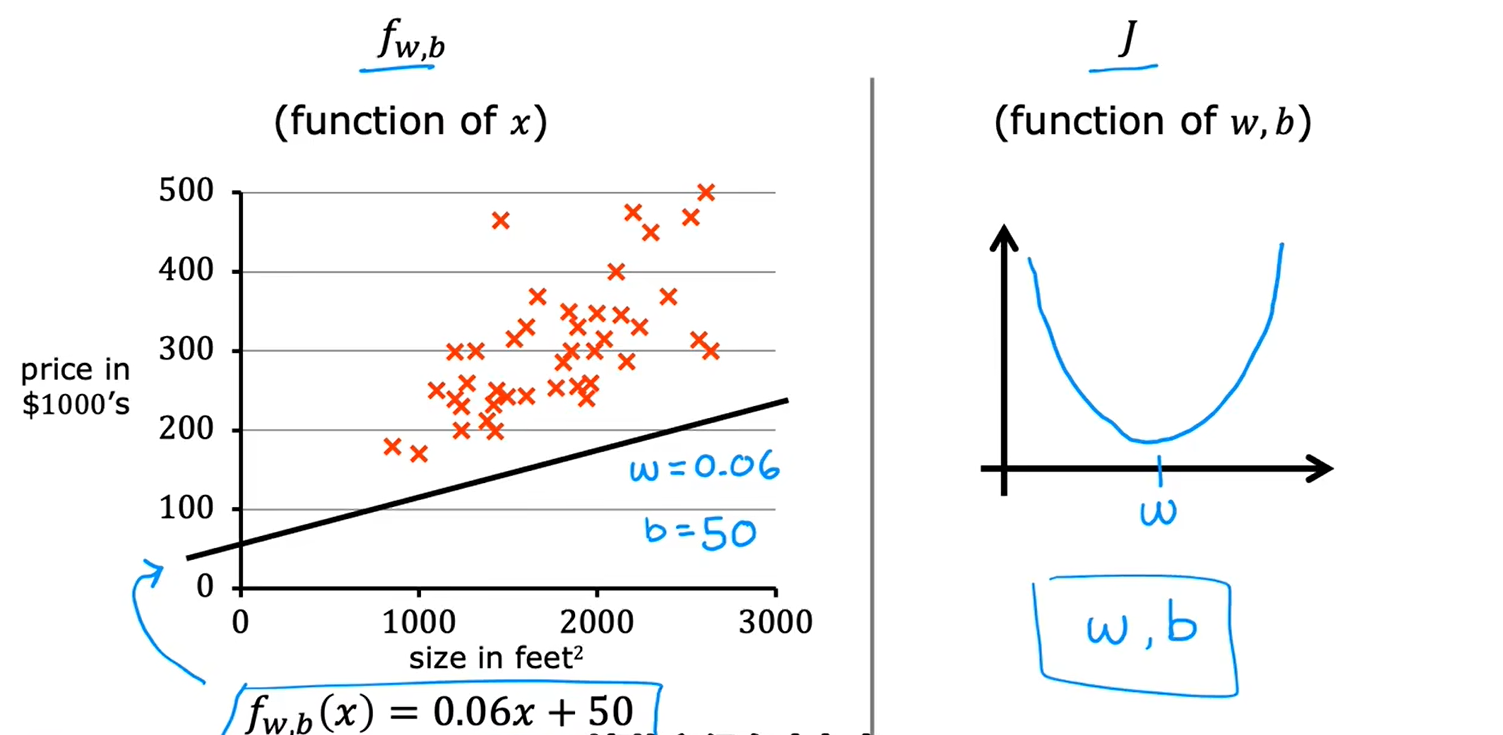
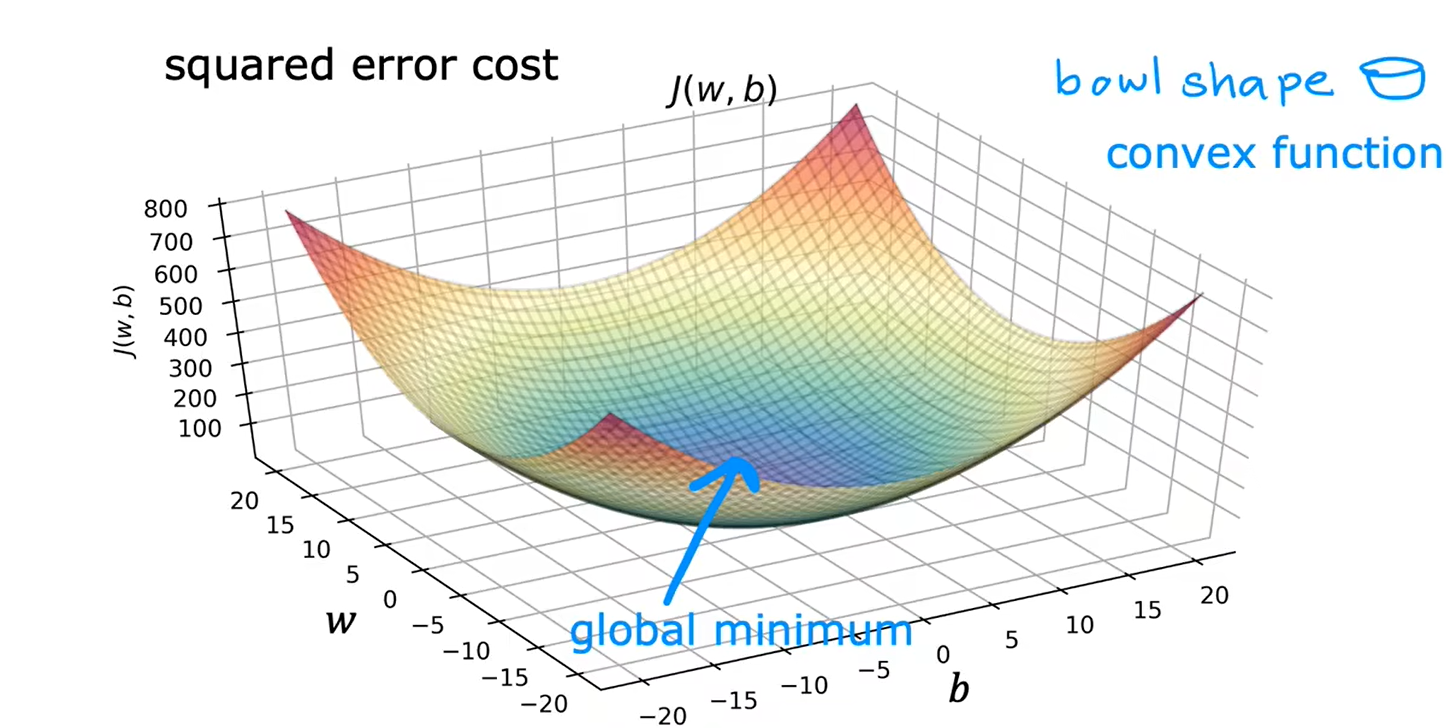
当有两个参数w和b时:

---

---

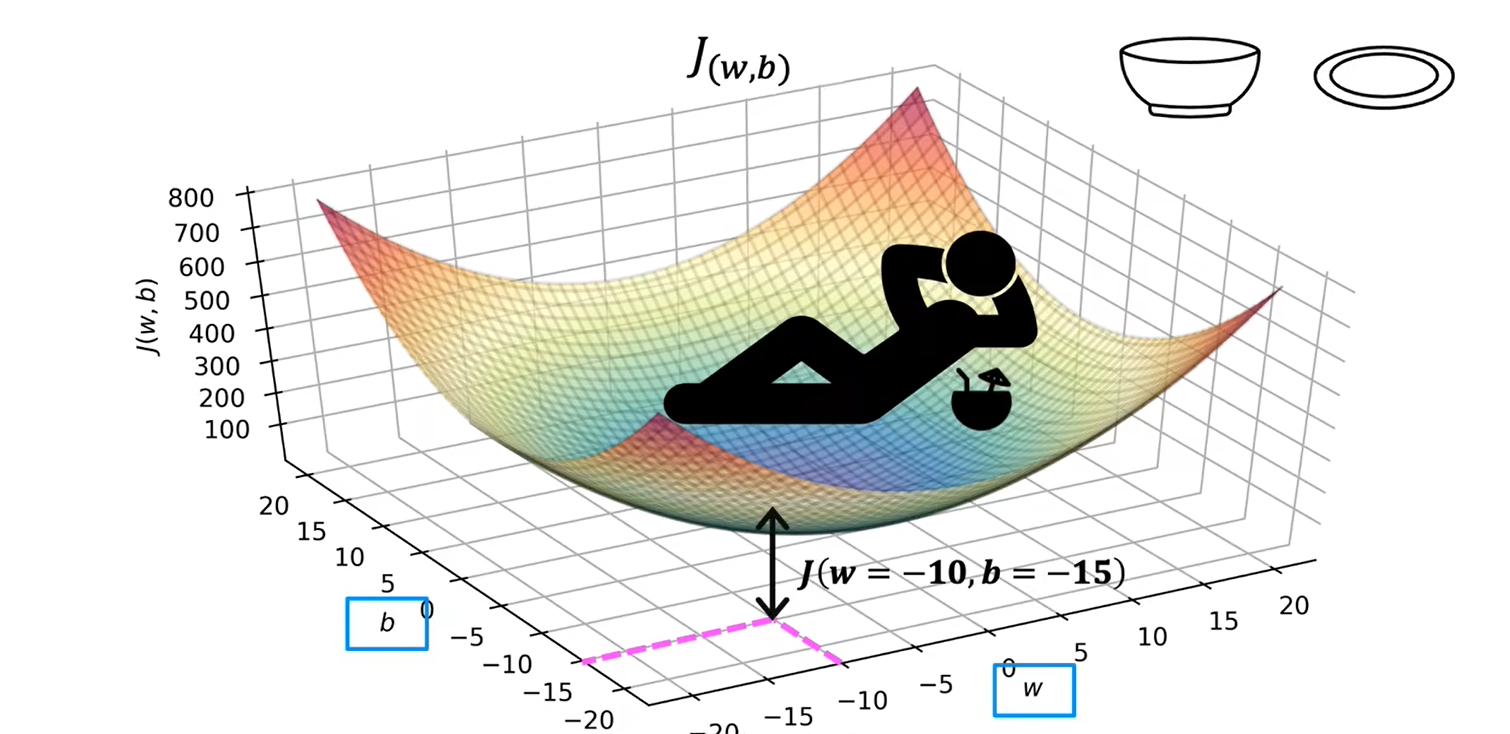
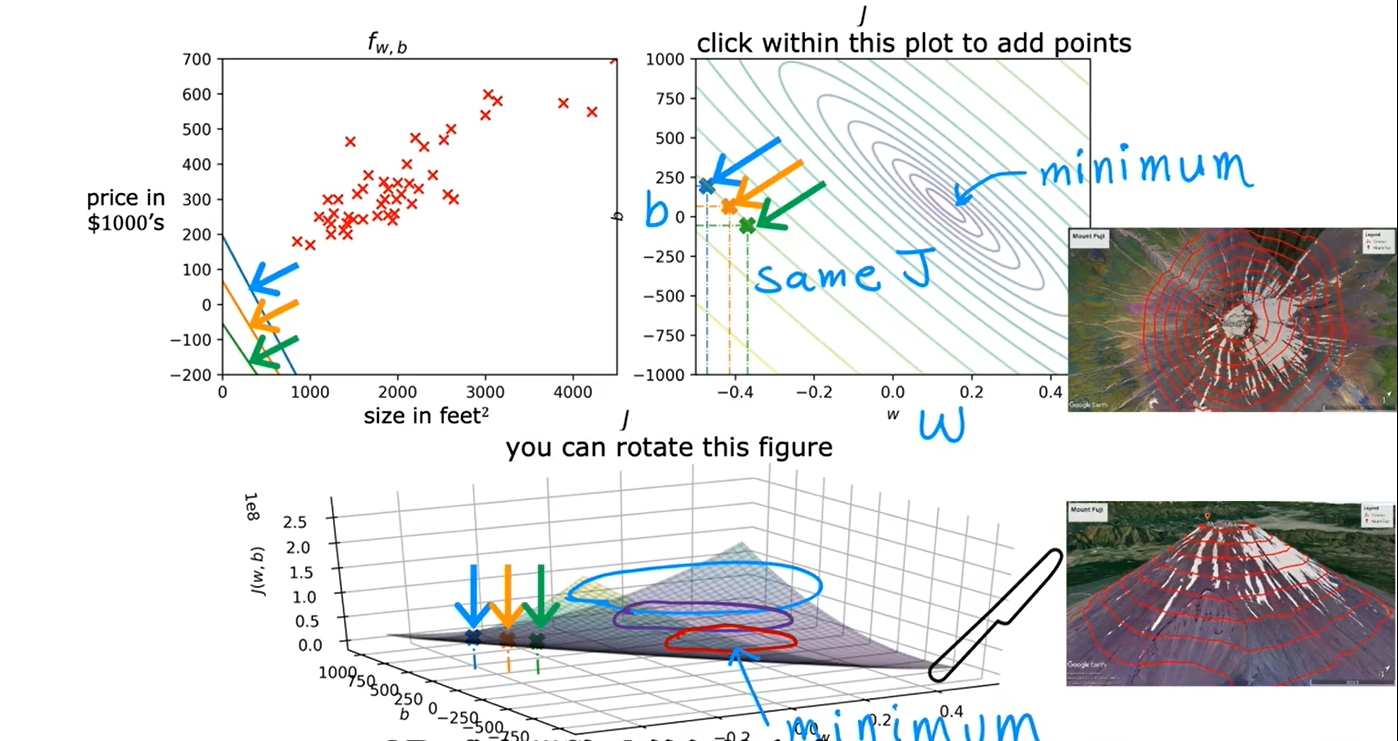
三、梯度下降

编写算法，能够自动找到w和b，最小化代价函数，使用梯度下降进行训练

1、梯度下降的实现

---

出现局部最小值：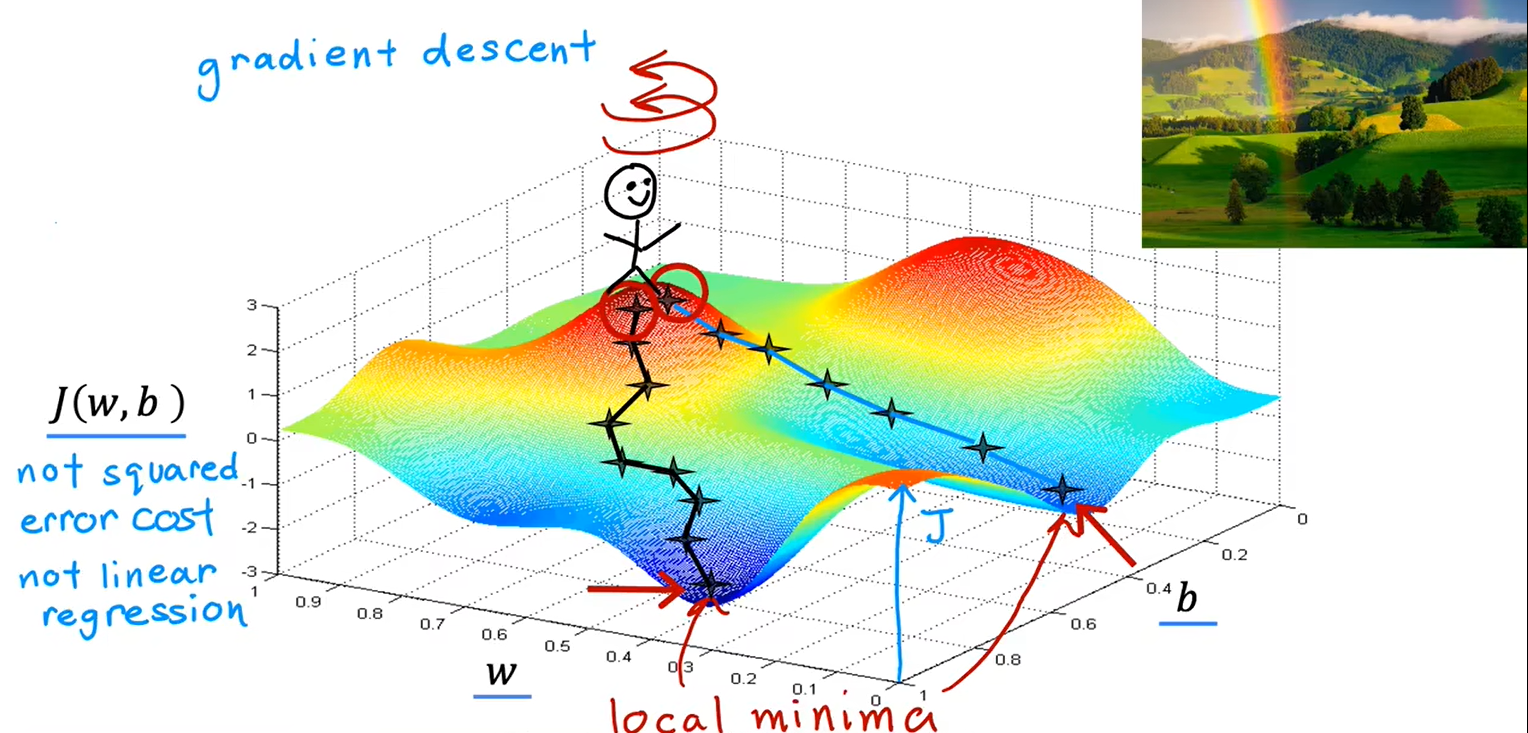

---

同步更新w和b:

---

2、理解梯度下降

---

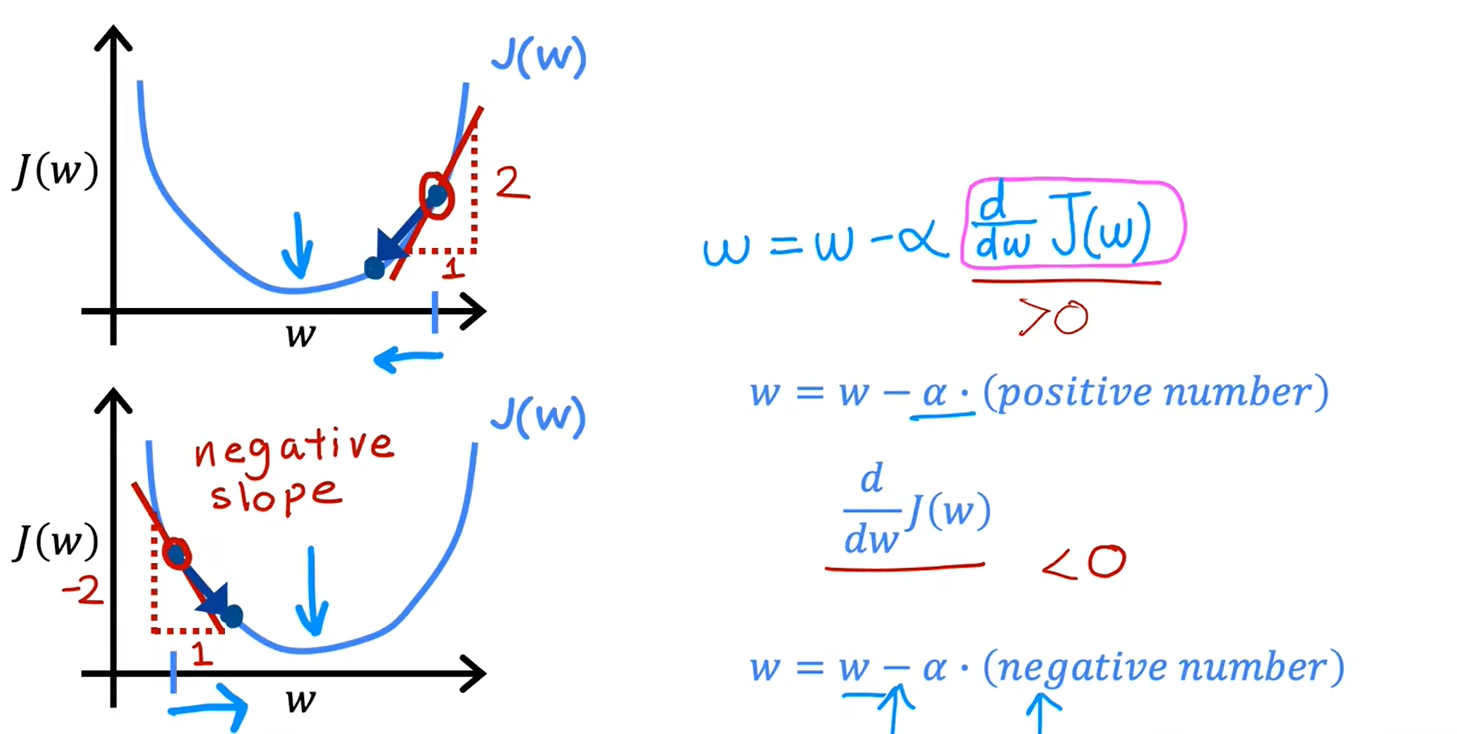
3、学习率

---

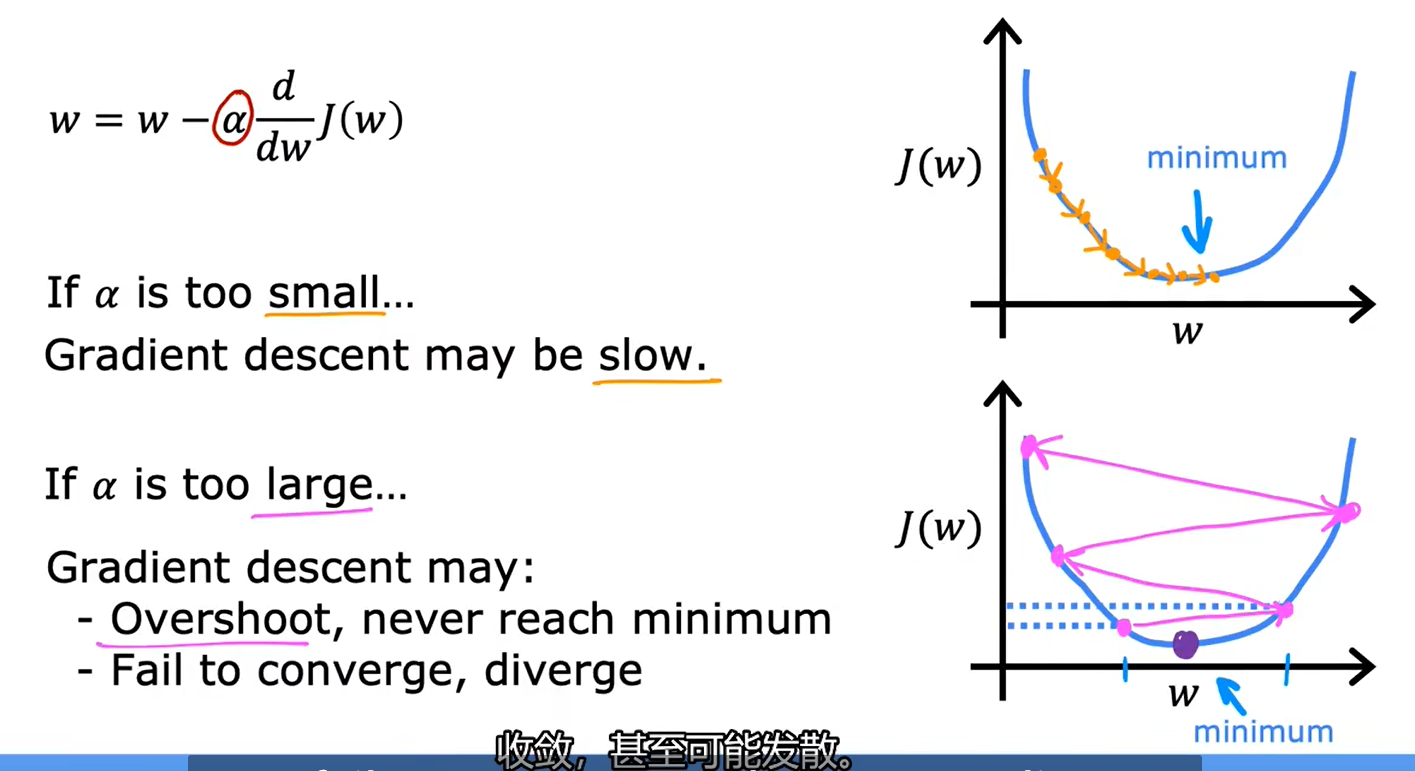
局部最小值：

---

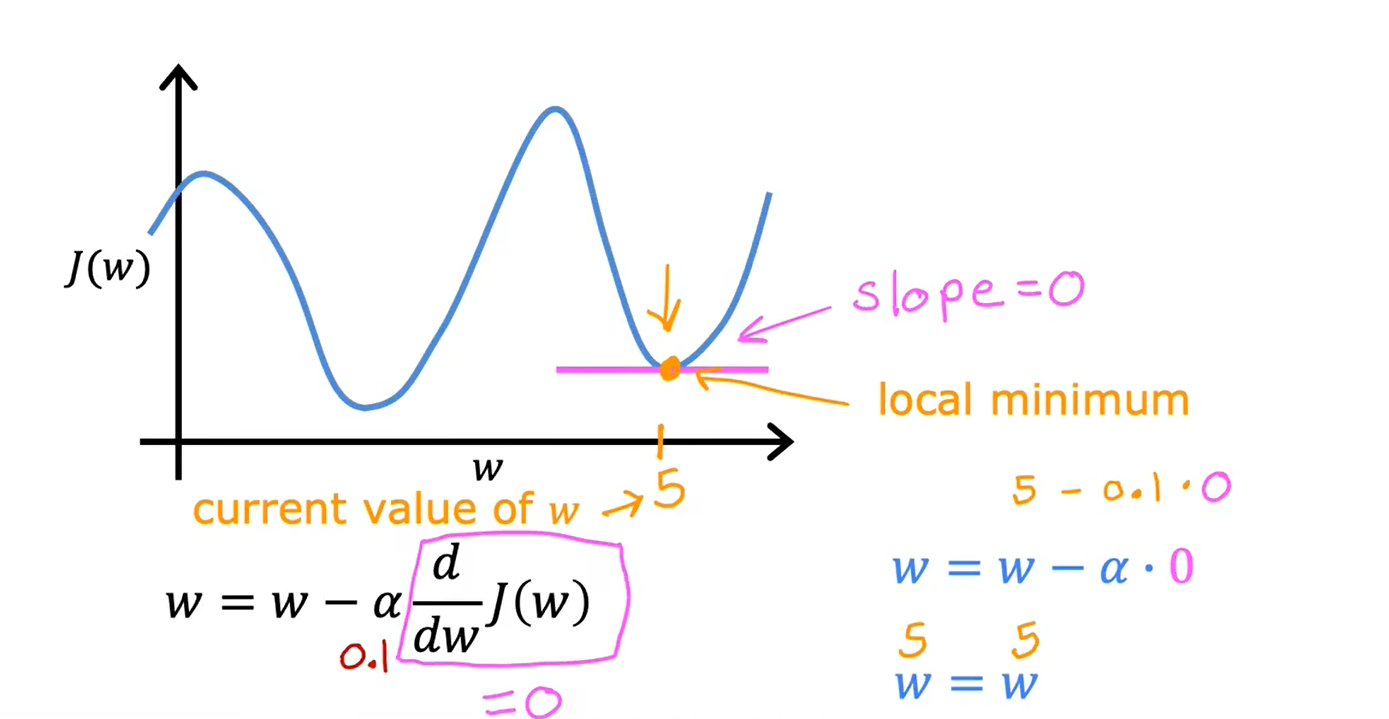
接近最小值，导数会自动变小，参数更新步伐变小：

---

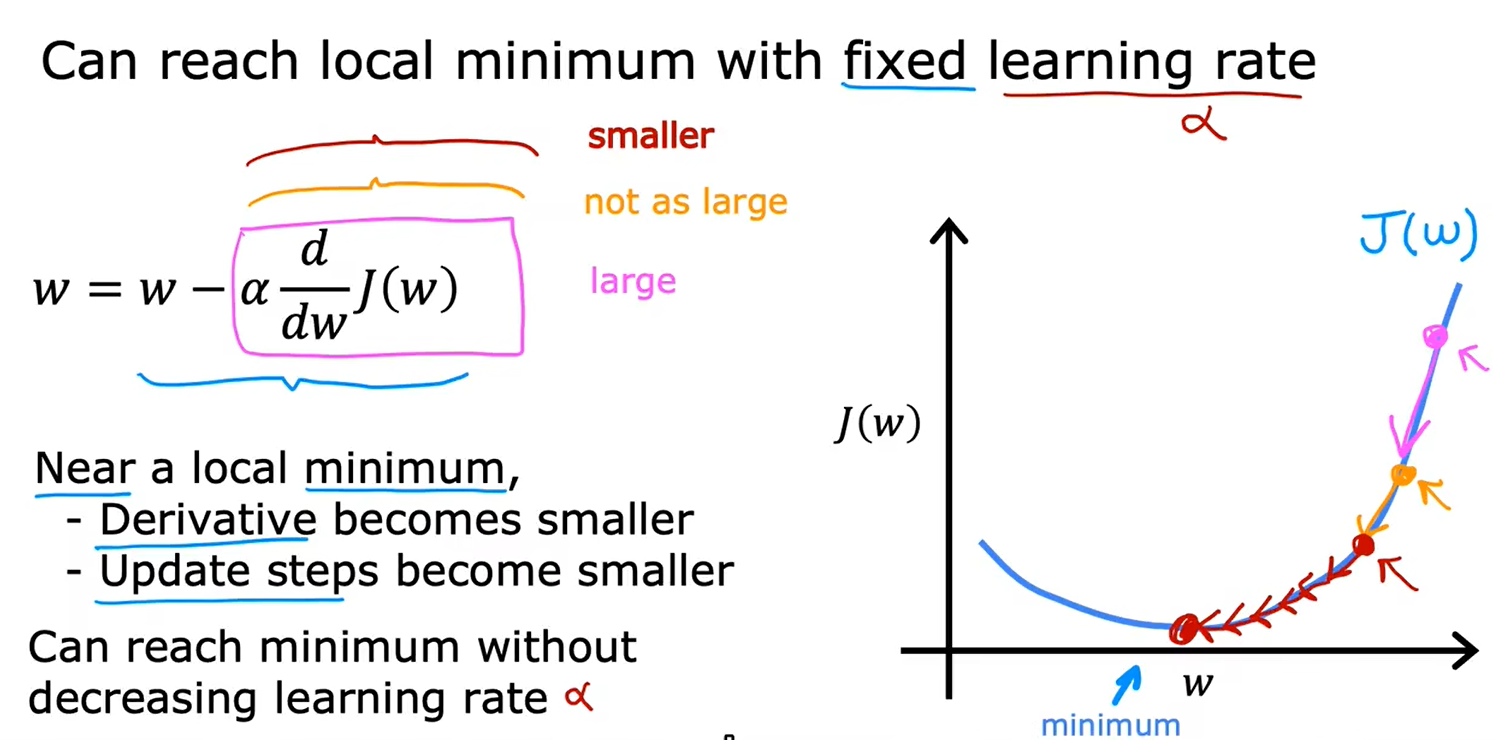
4、导数更新过程

---

---

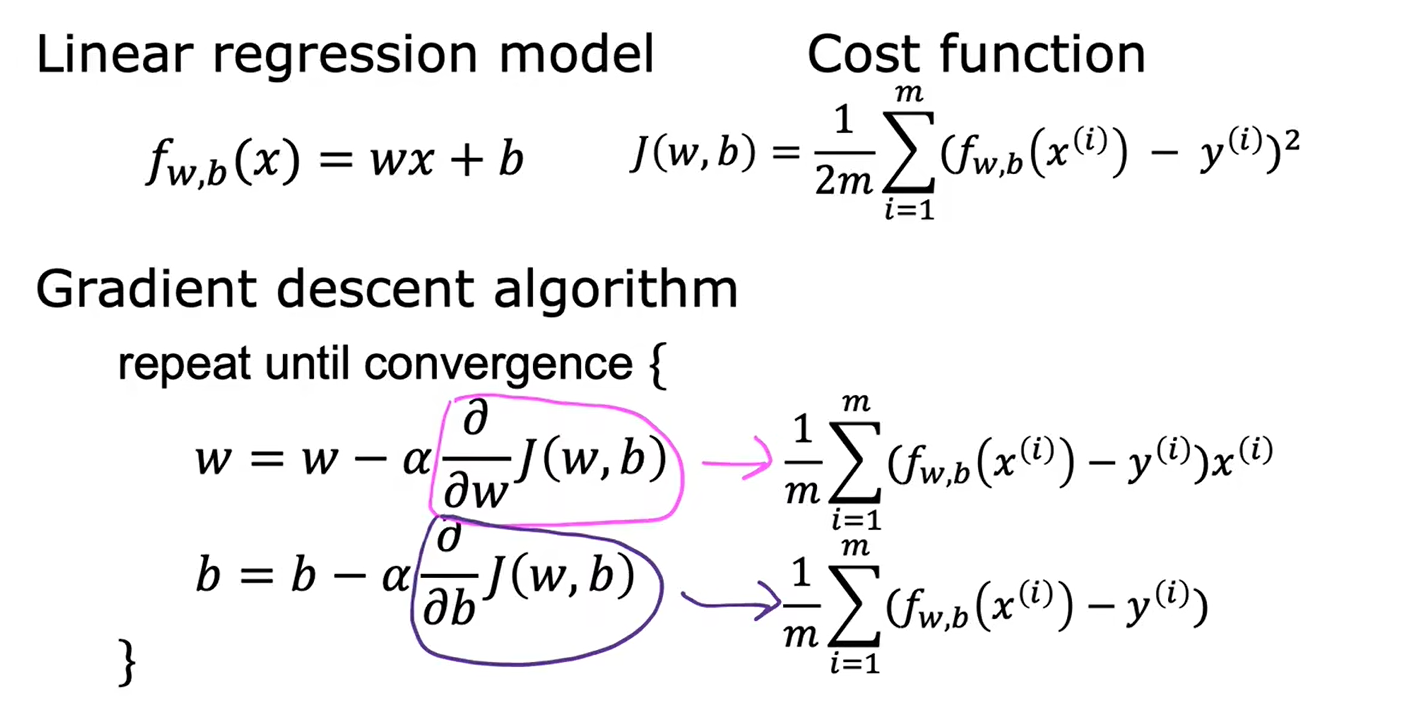
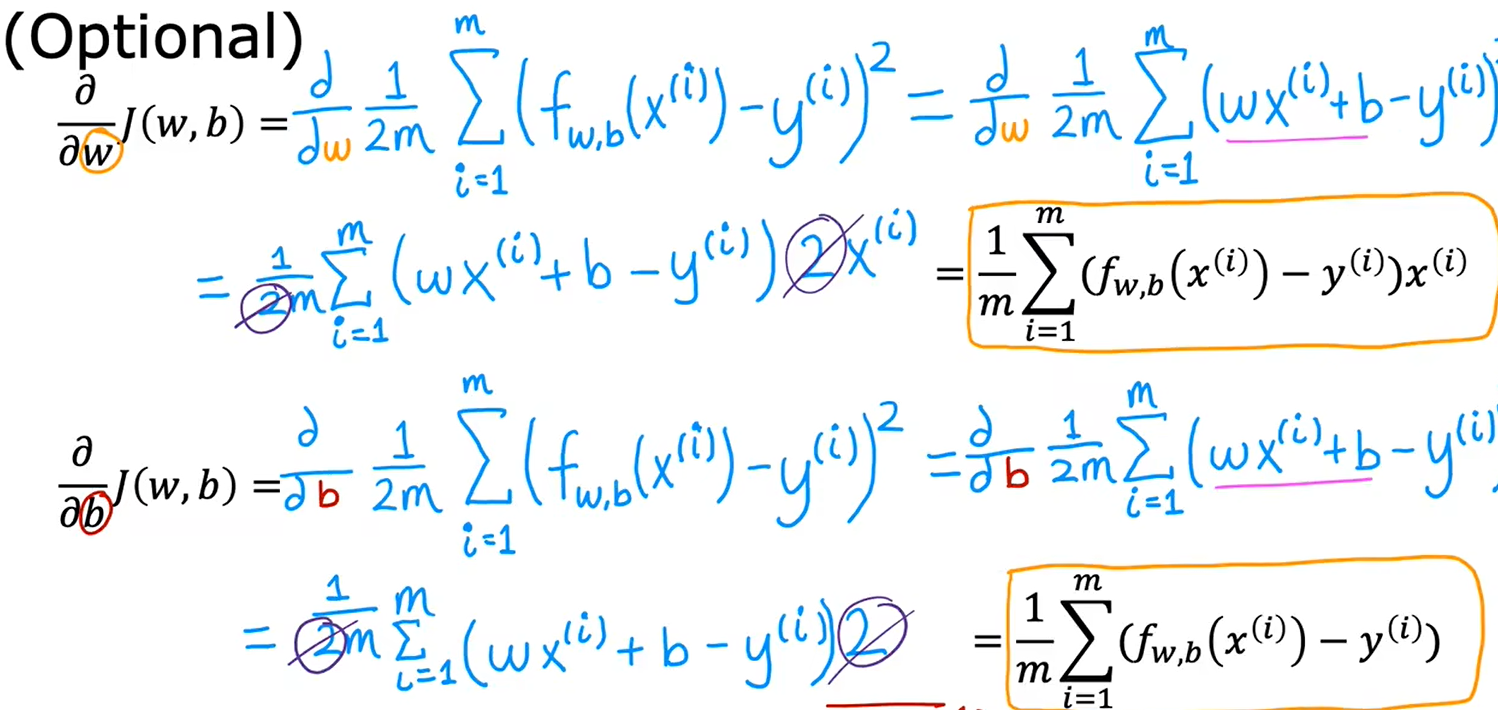
用于线性回归的梯度下降，代价函数不会出现多个局部最小值，只会有一个全局最小值，图像是一个凸函数

---

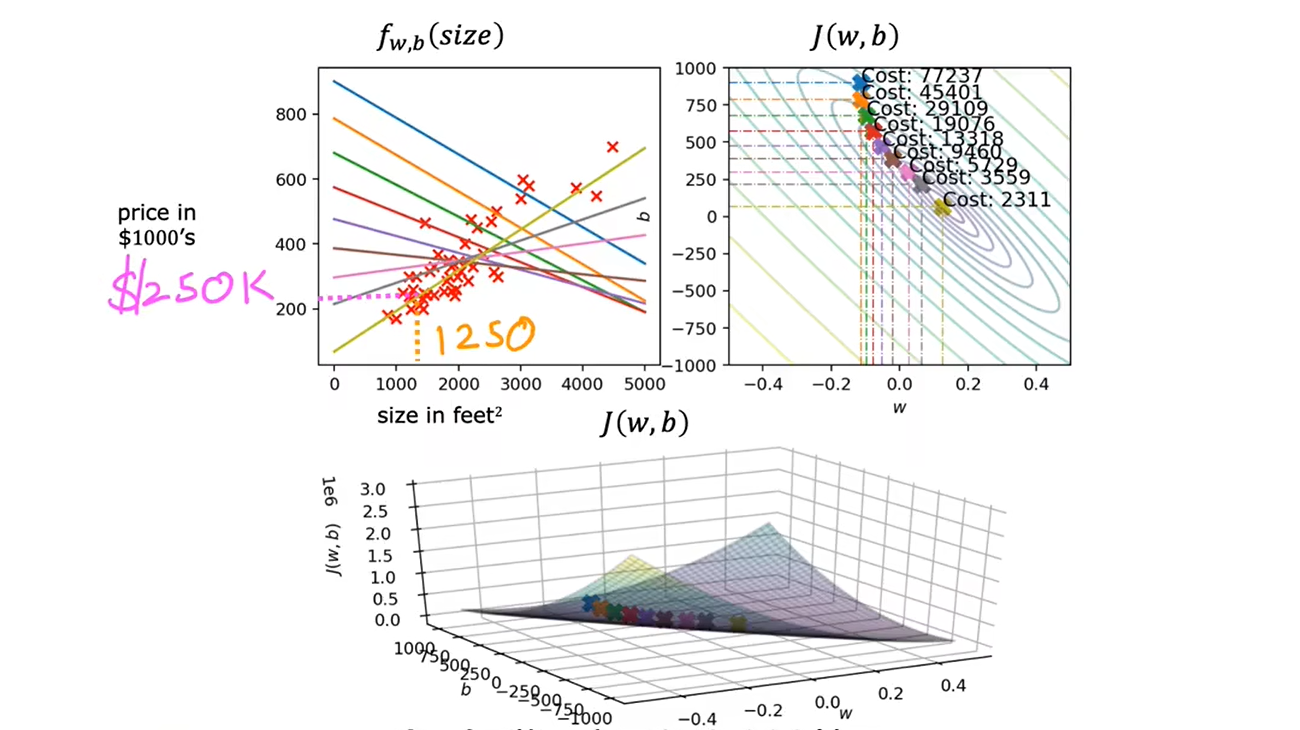
5、运行梯度下降

---

第二周

一、向量化

1.1多维特征

---

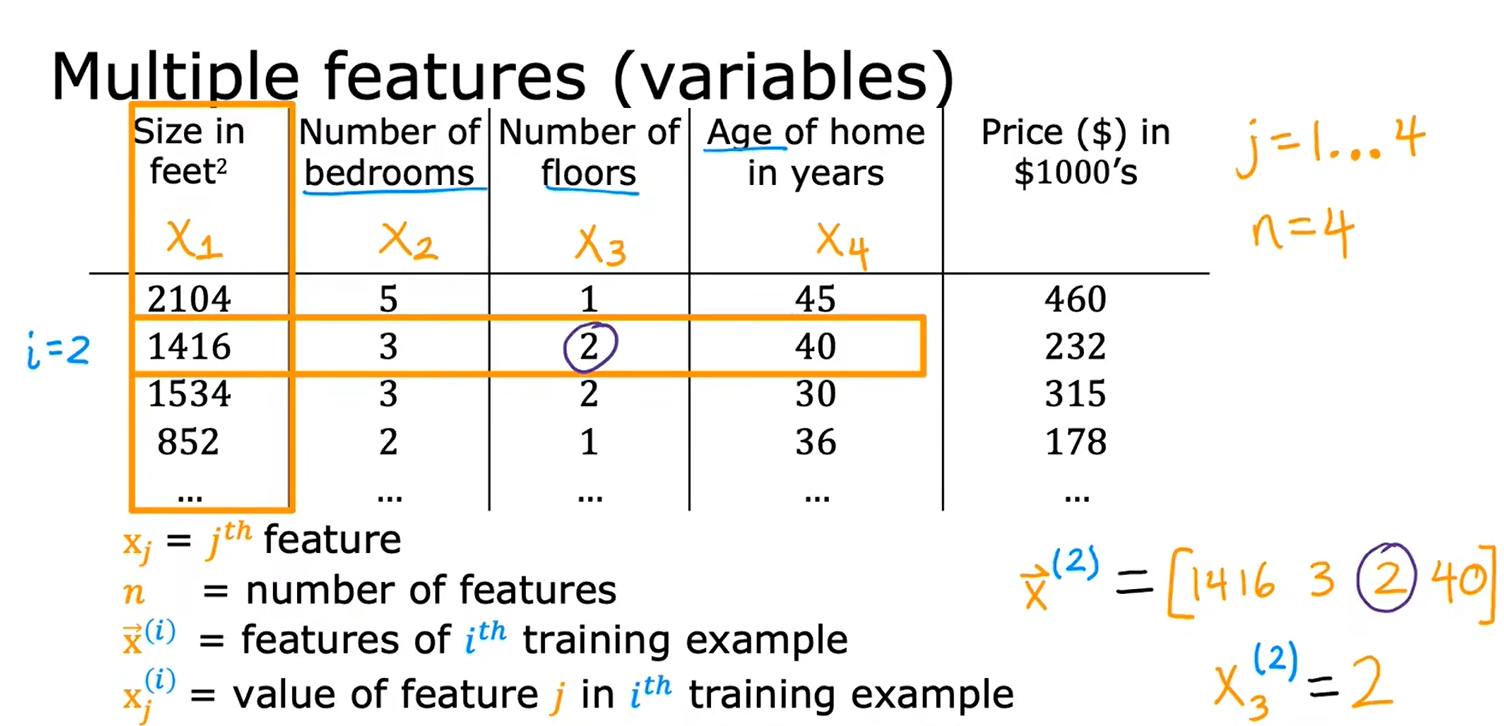
含有n个特征的模型的定义：

---

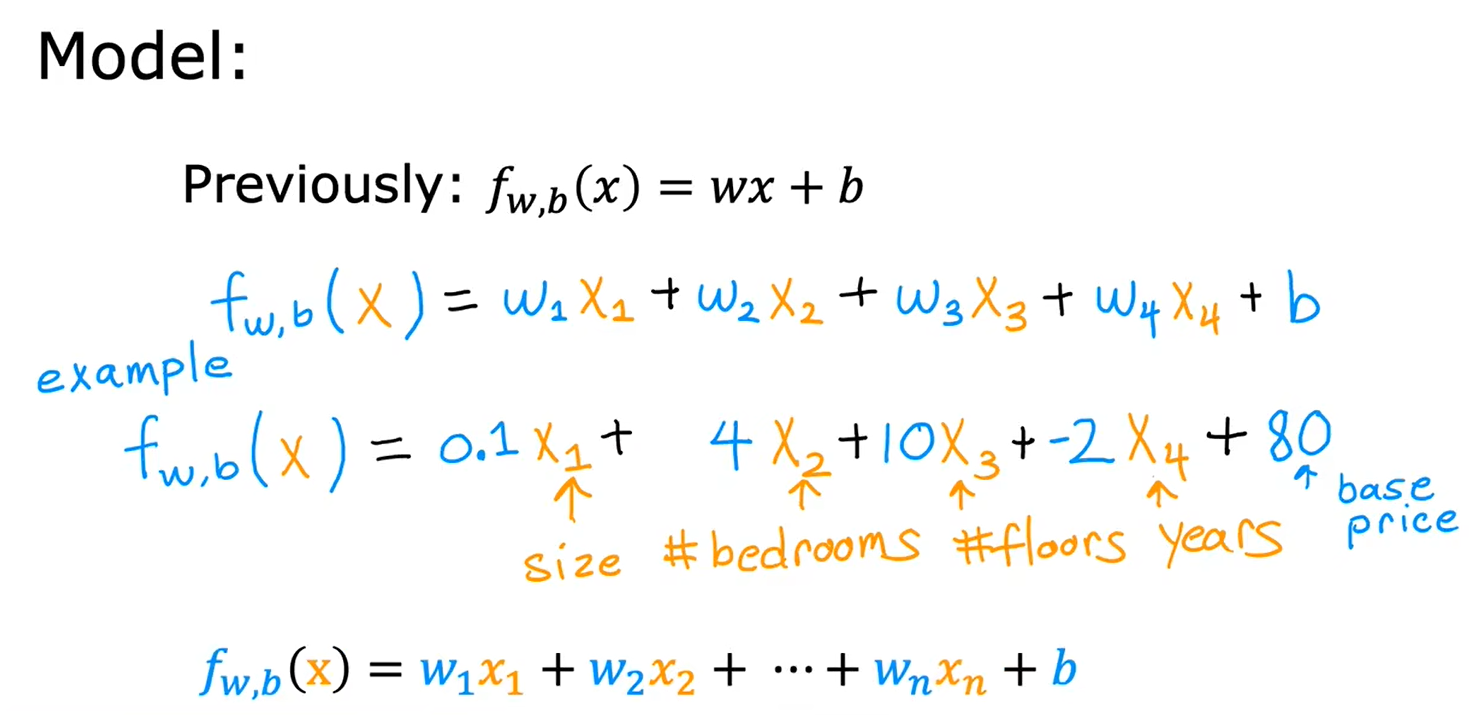
多元线性回归模型：

---

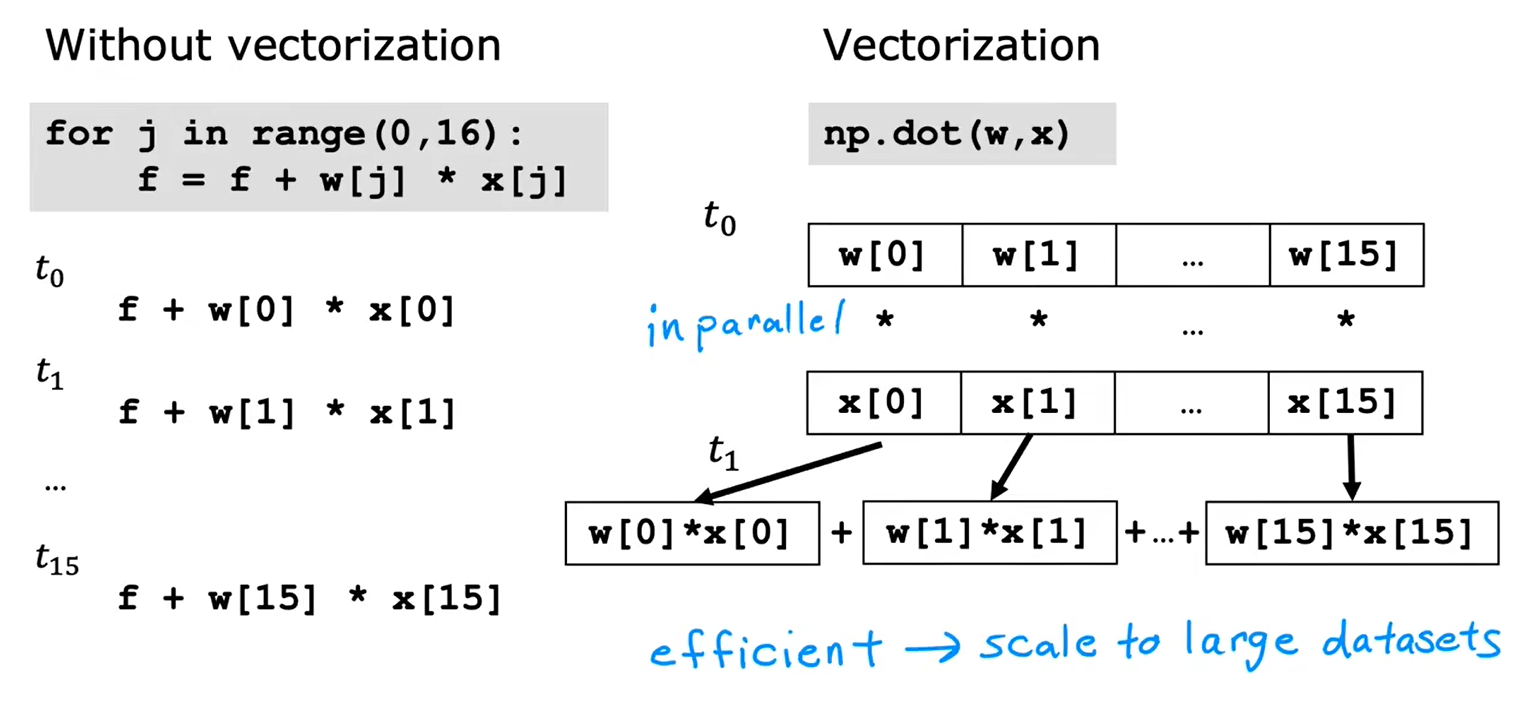
1.2向量化-part1

---

1.3向量化-part2

使用Numpy的点积运算，效率更高

---

---

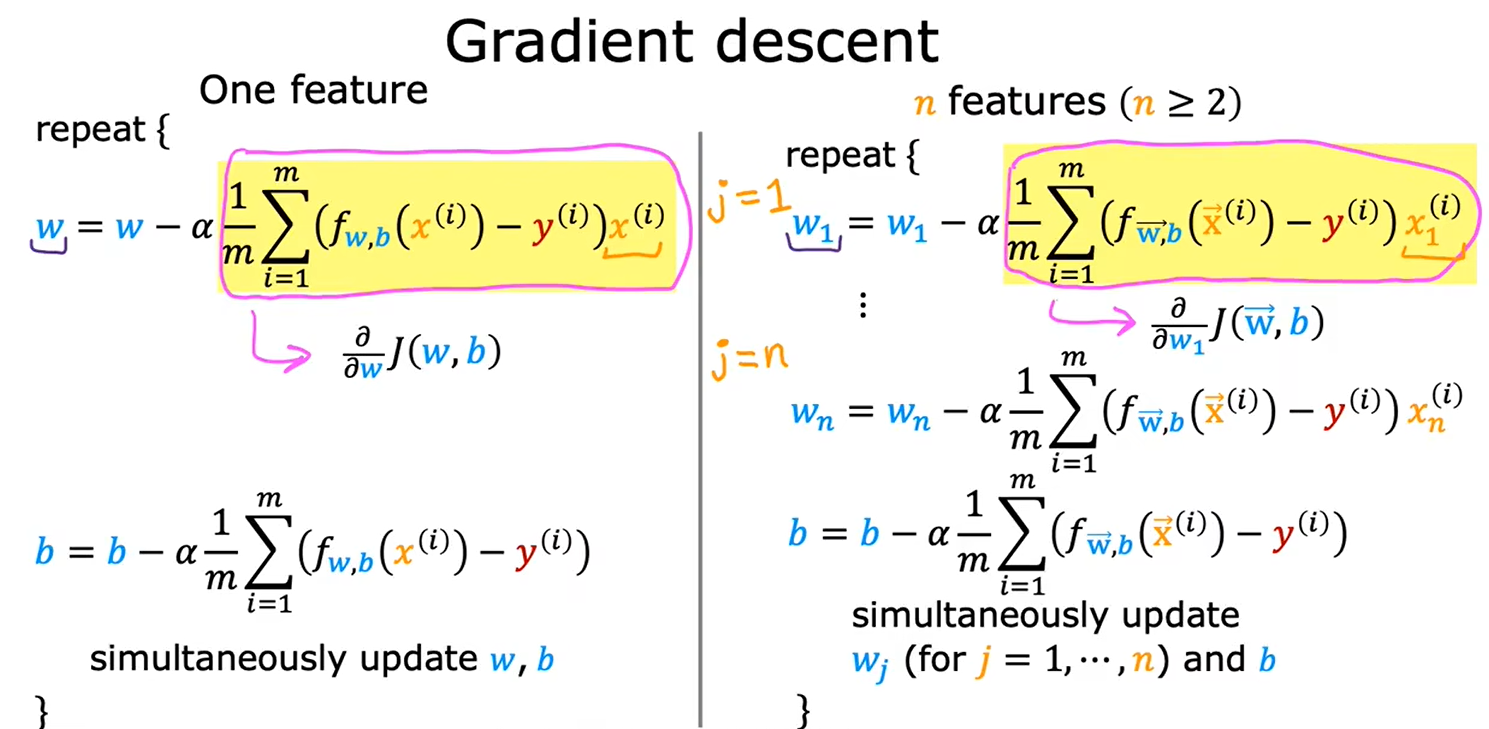
1.4用于多元线性回归的梯度下降法

---

二、特征缩放

2.1特征缩放-part1

---

---

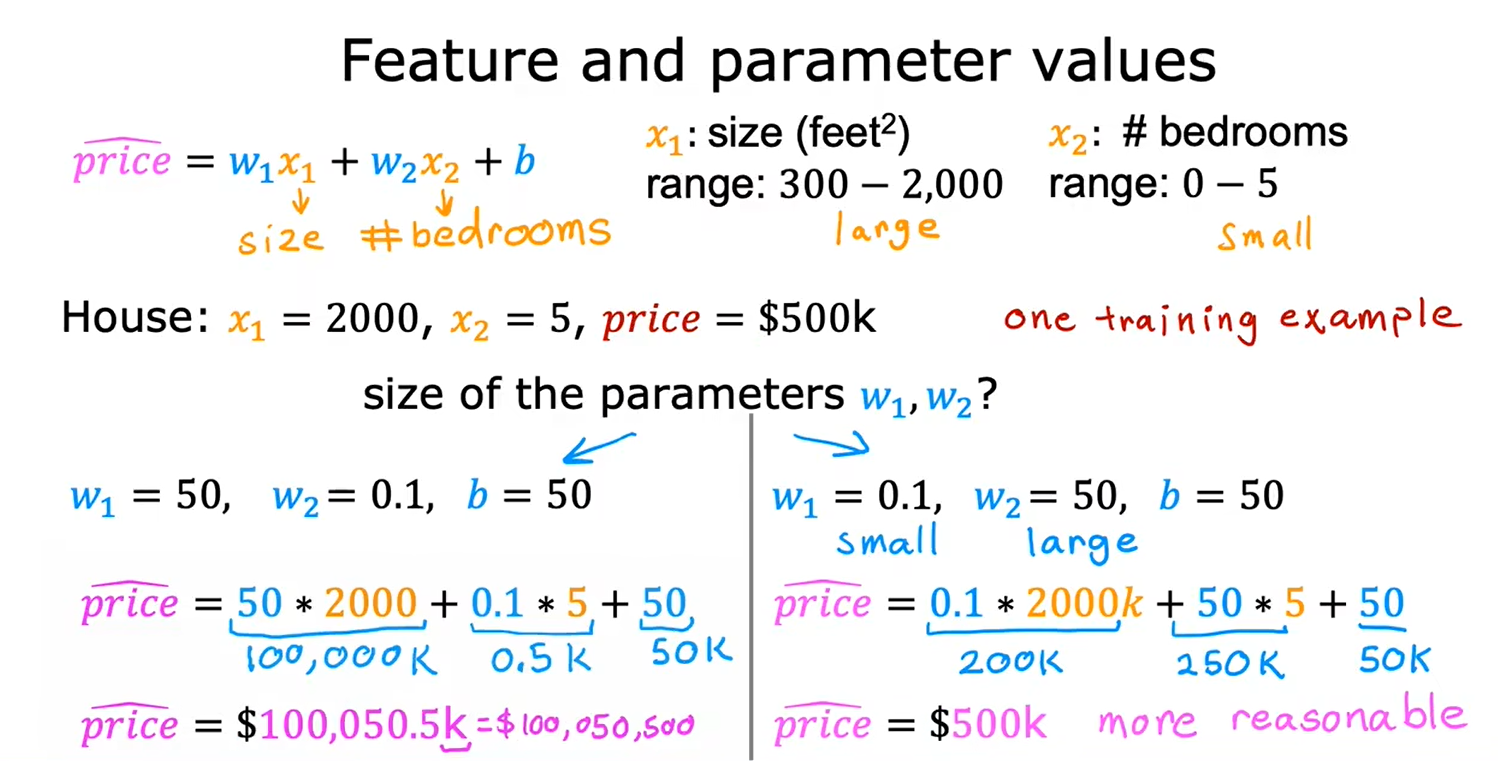
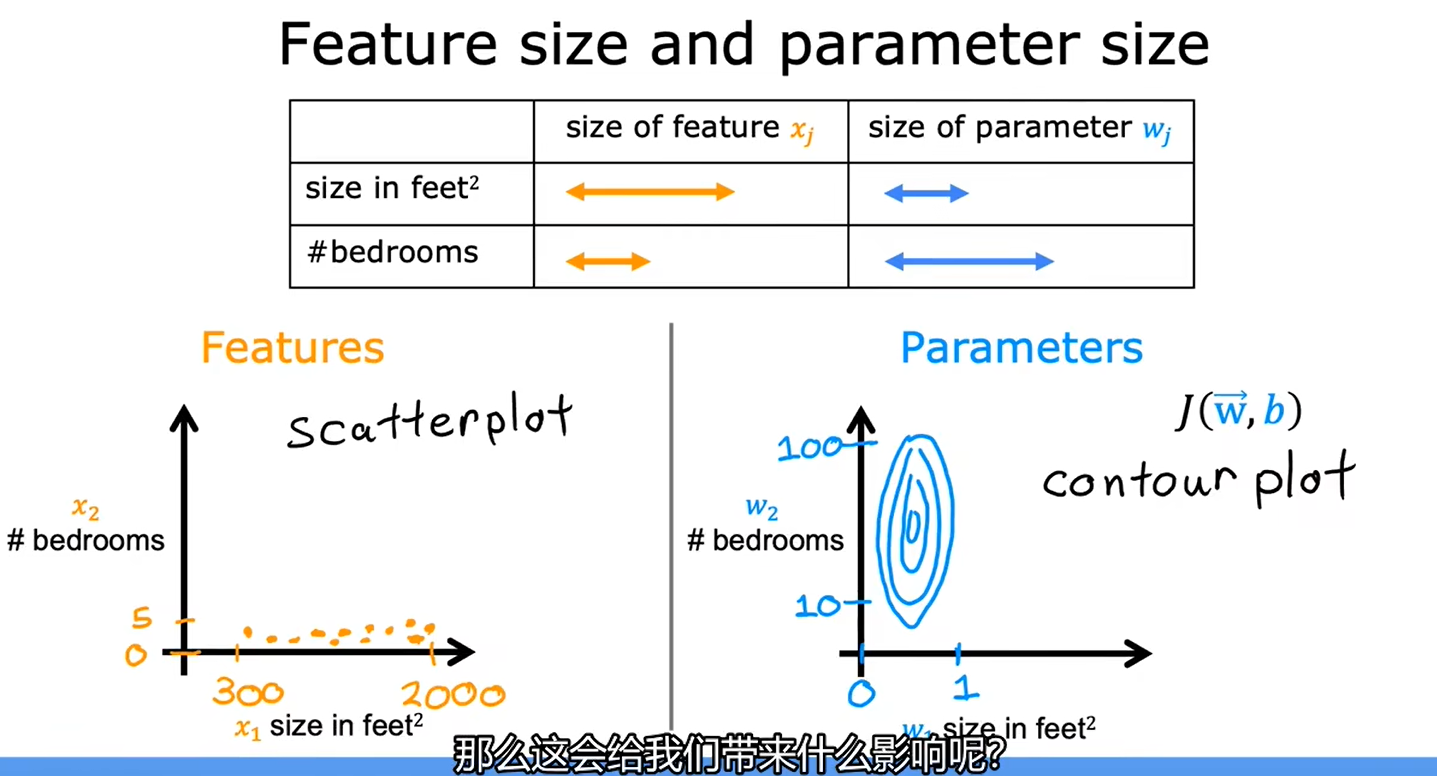
重新缩放这些特征，使它们具有可比较的值的范围，可以显著加快梯度下降速度

---

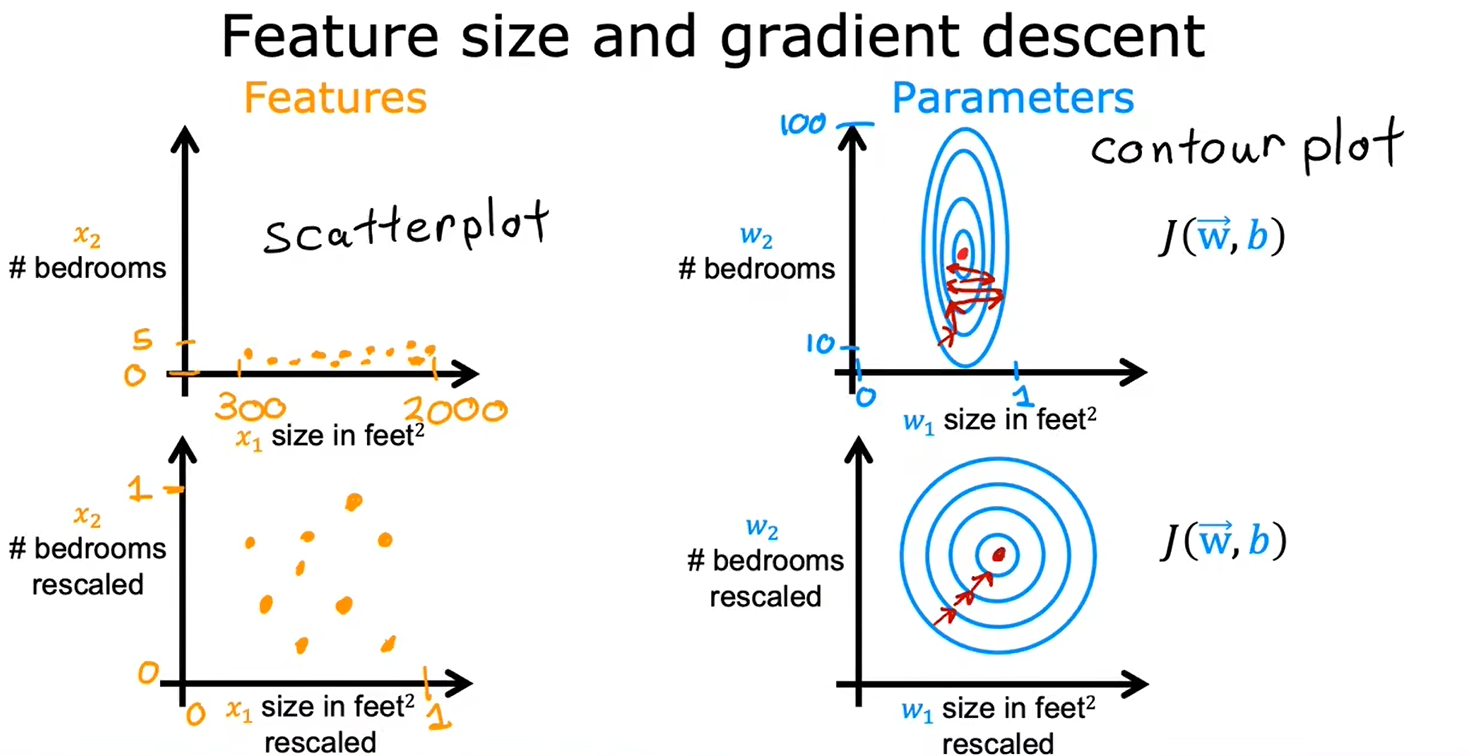
2.2特征缩放-part2
最大值归一化

---

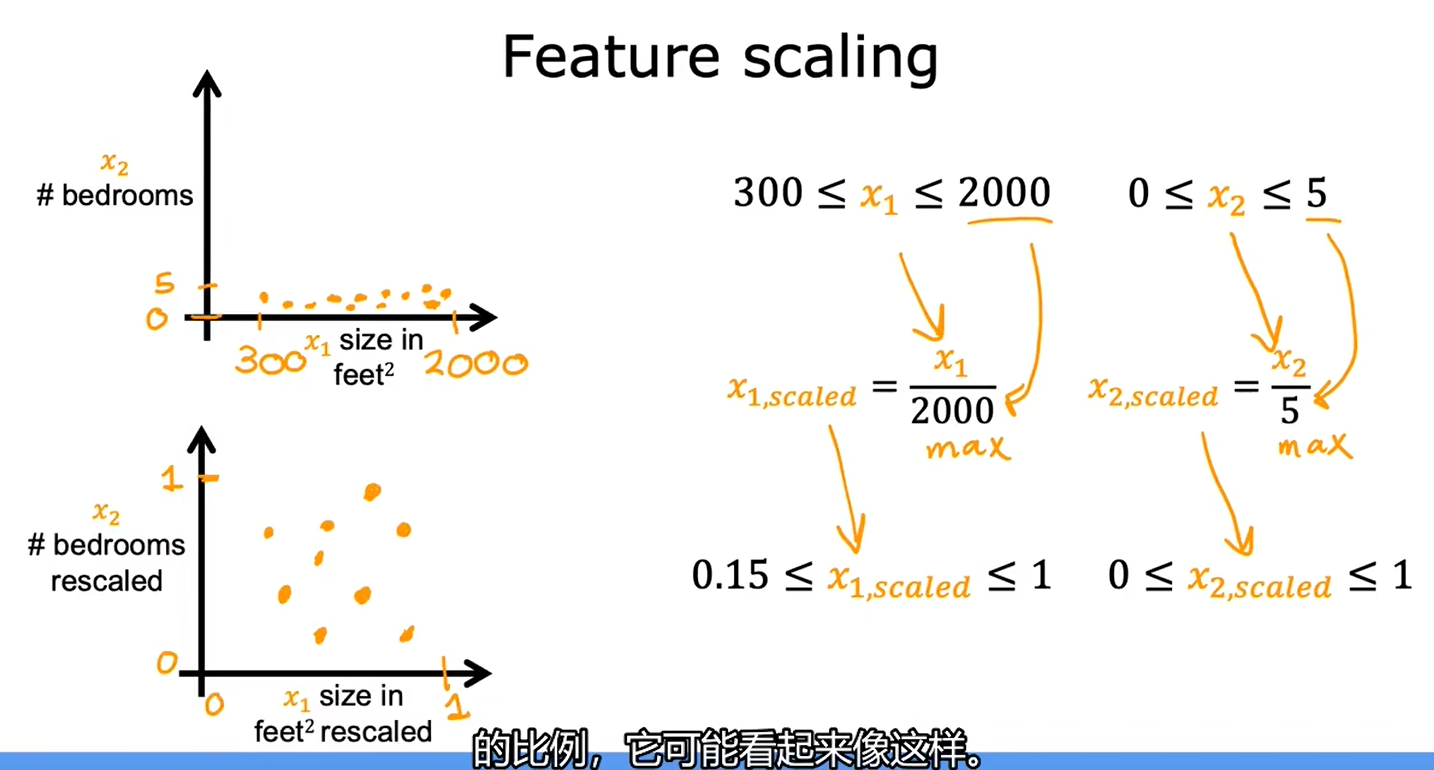
均值归一化

---

Z-Score归一化

---

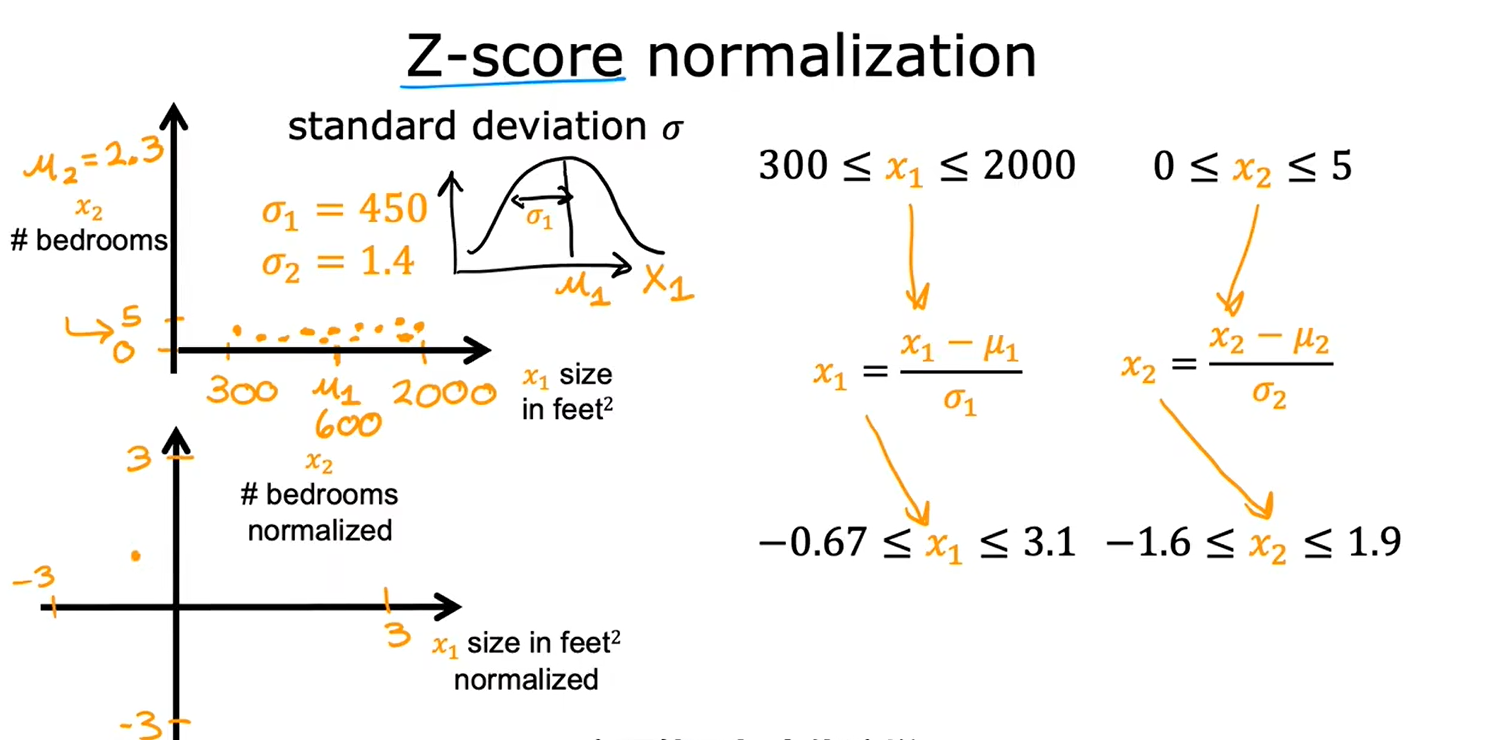
当数据差别较大时，最好进行特征缩放

---

2.3判断梯度下降是否收敛

---

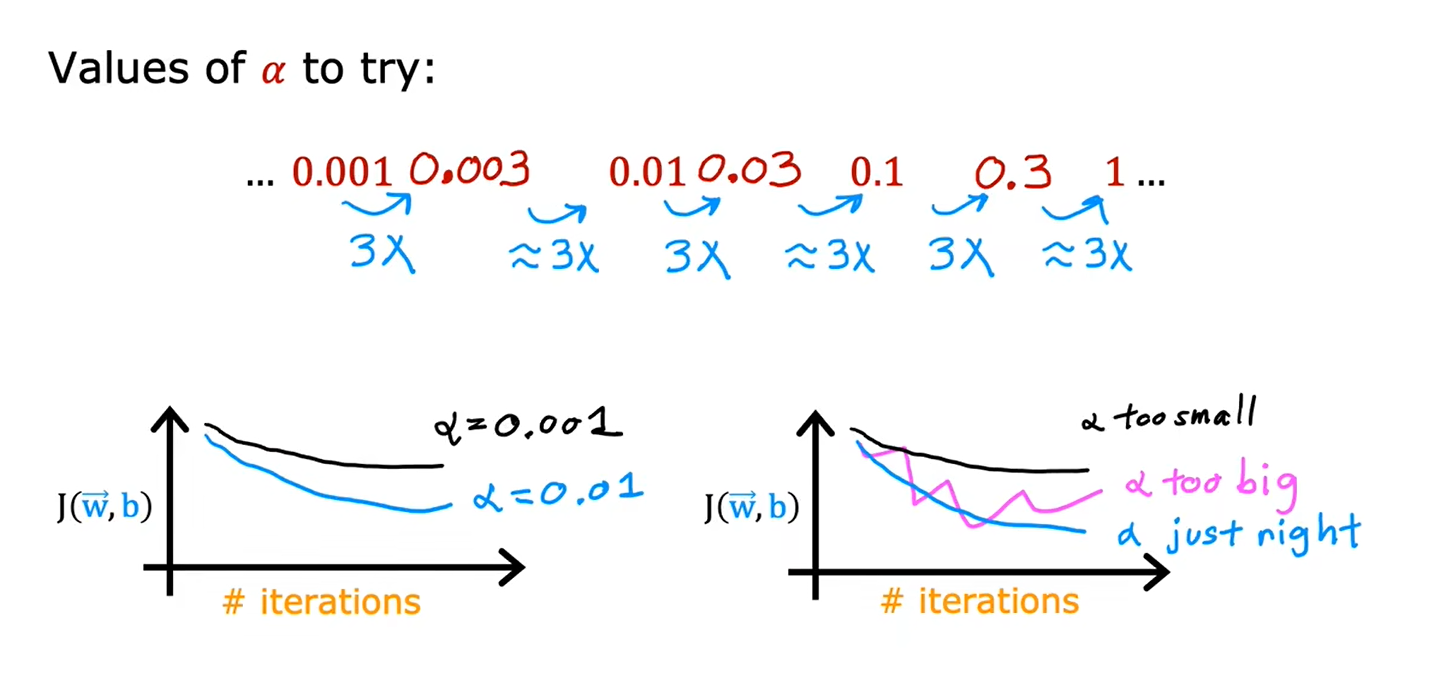
2.4如何设置学习率
当把α设置为很小的值时，发现损失函数J的值还会增大，说明是程序出现了bug

---

---

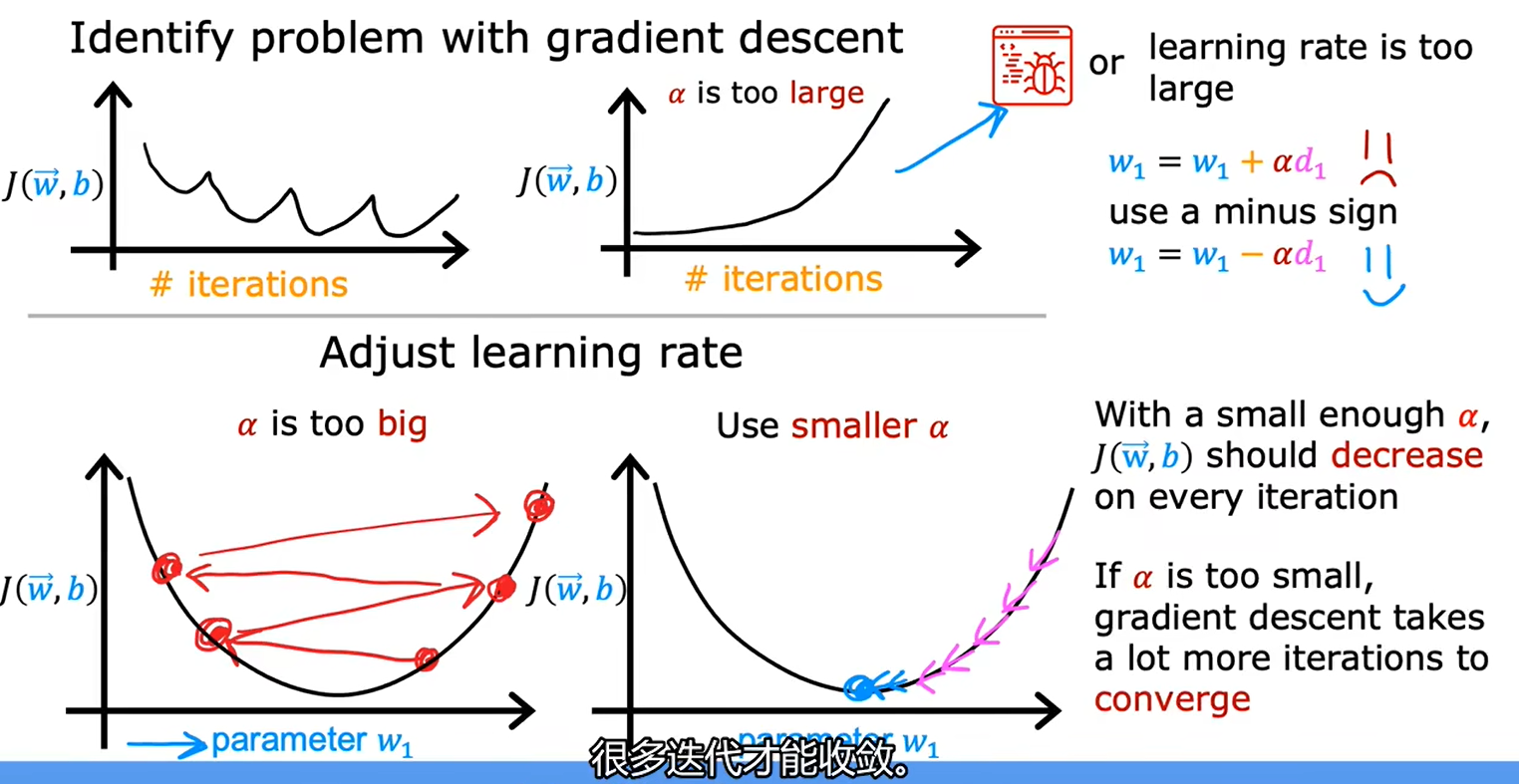
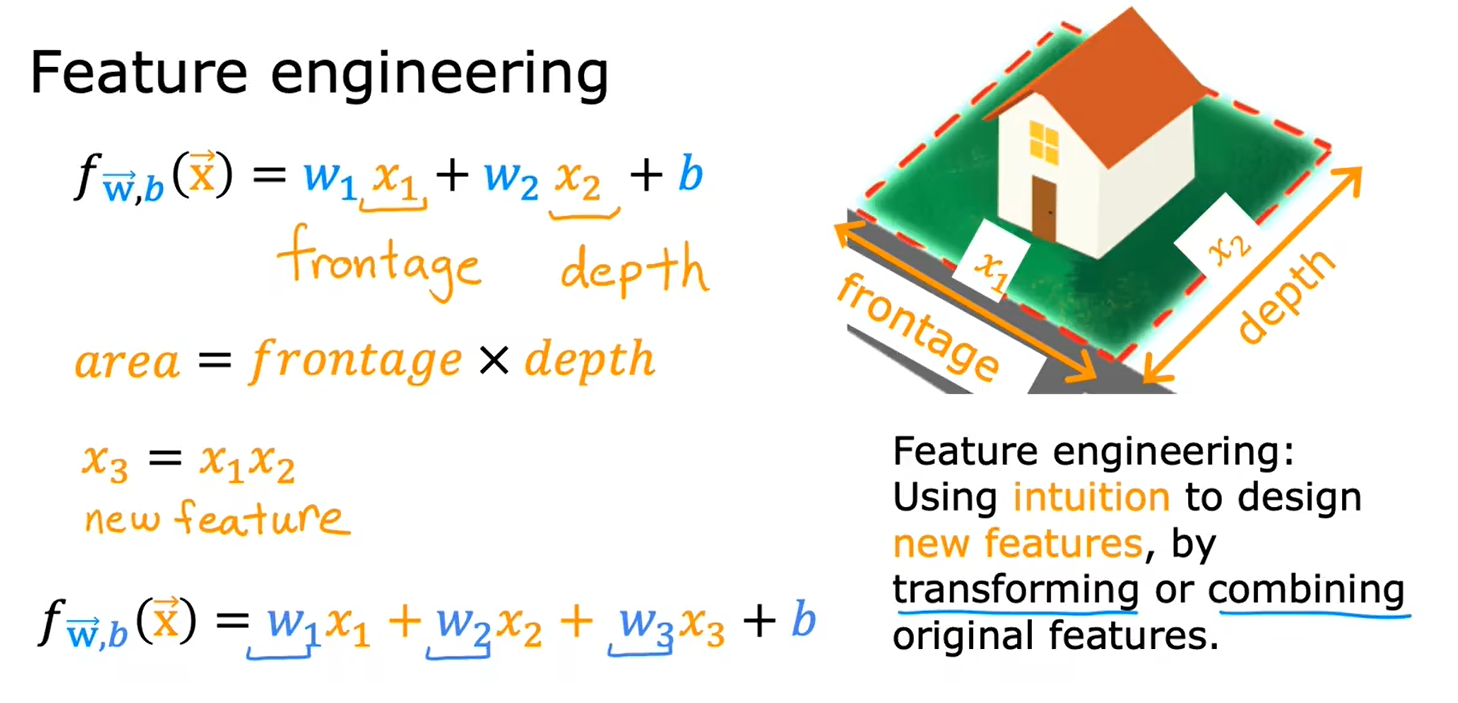
2.5特征工程

---

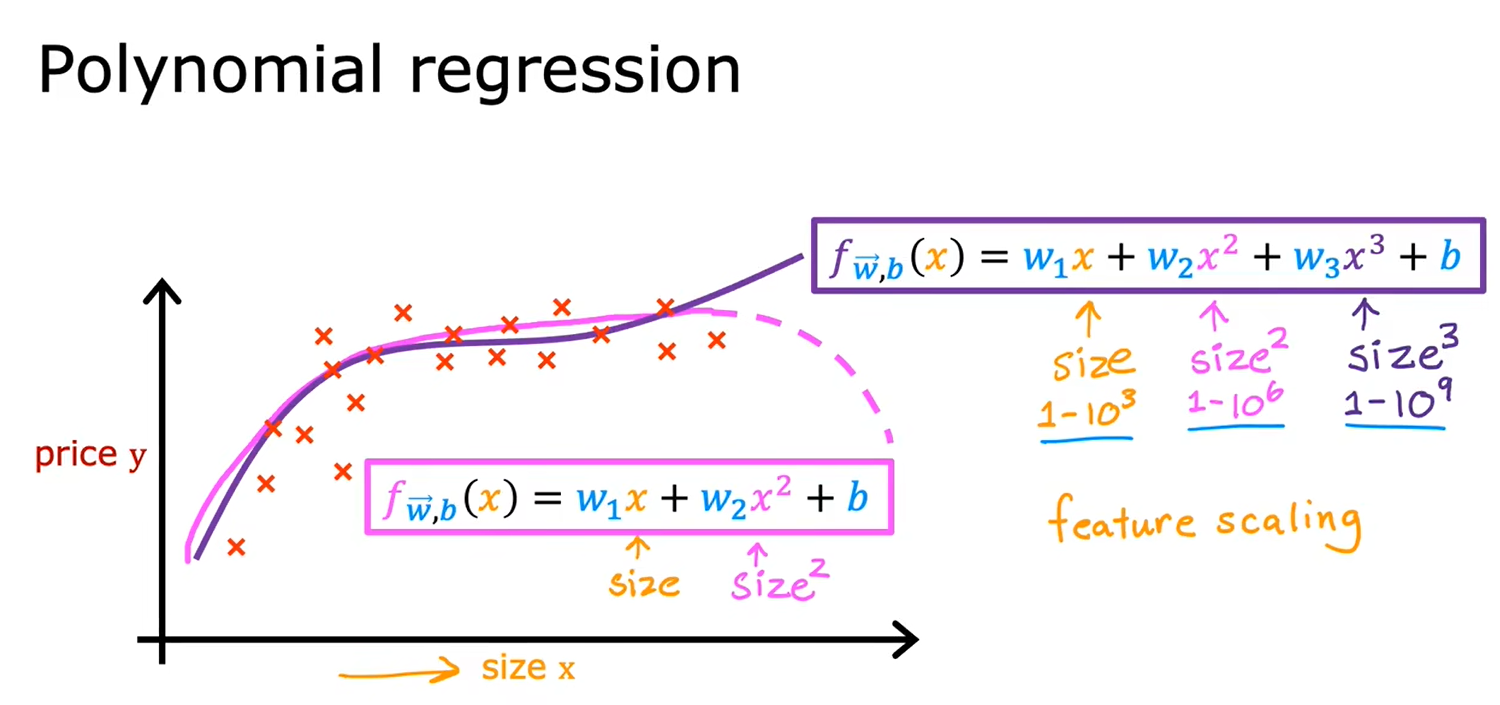
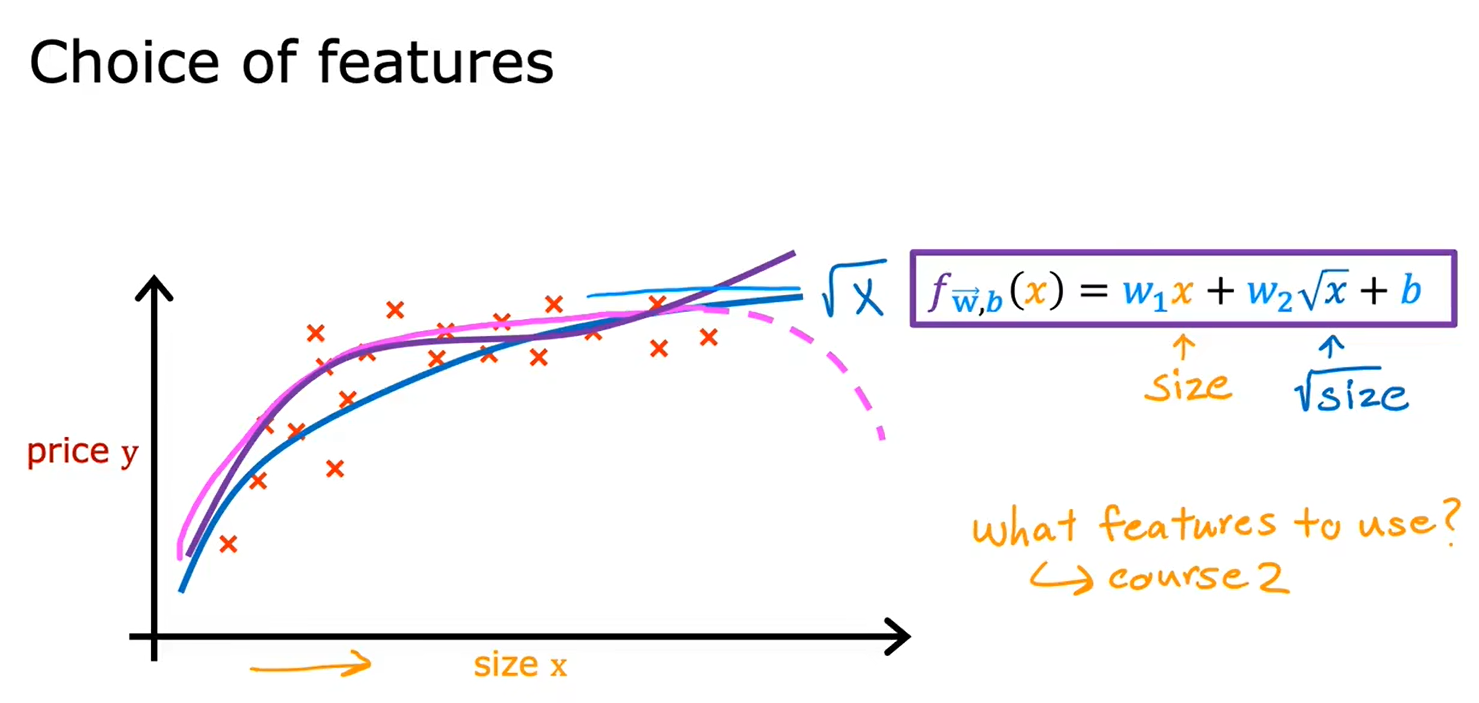
2.6多项式回归

---

---

第三周

一、逻辑回归

1.1分类

---

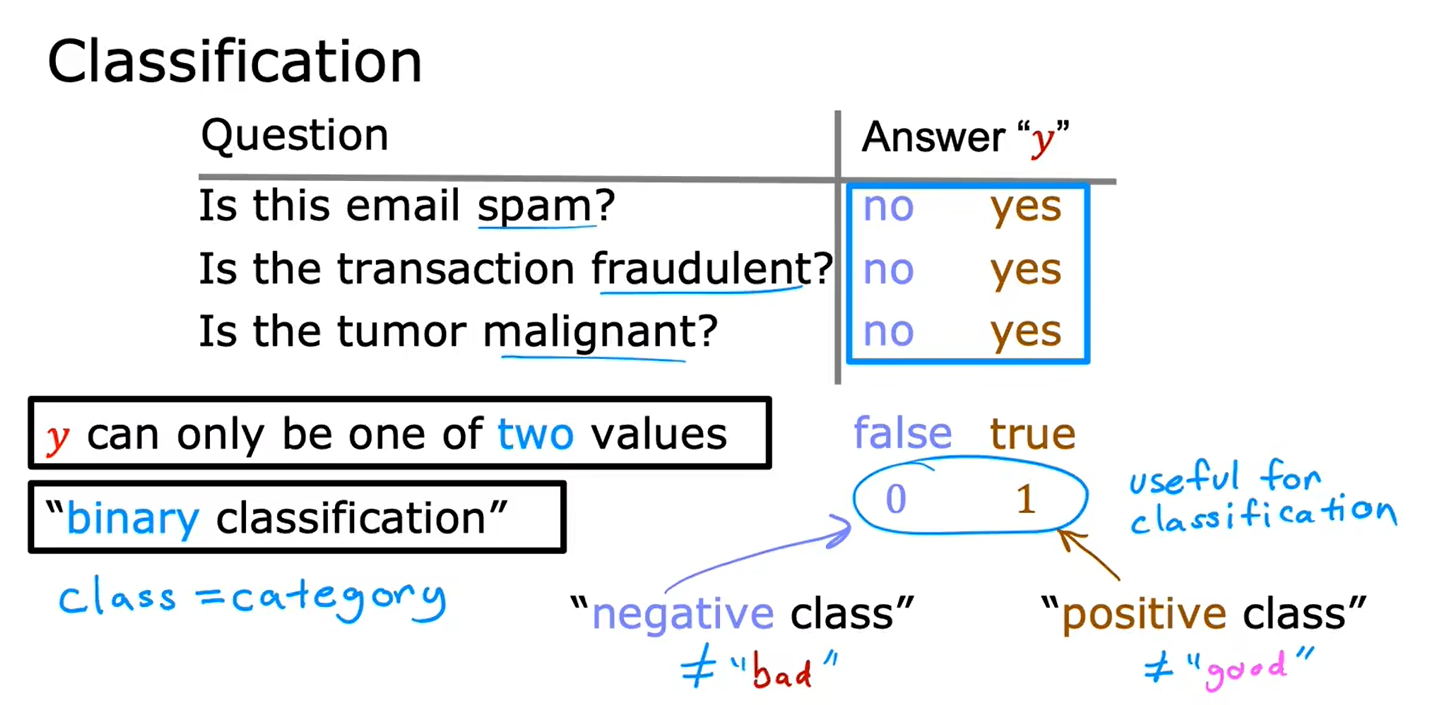
线性回归不适合于分类问题

---

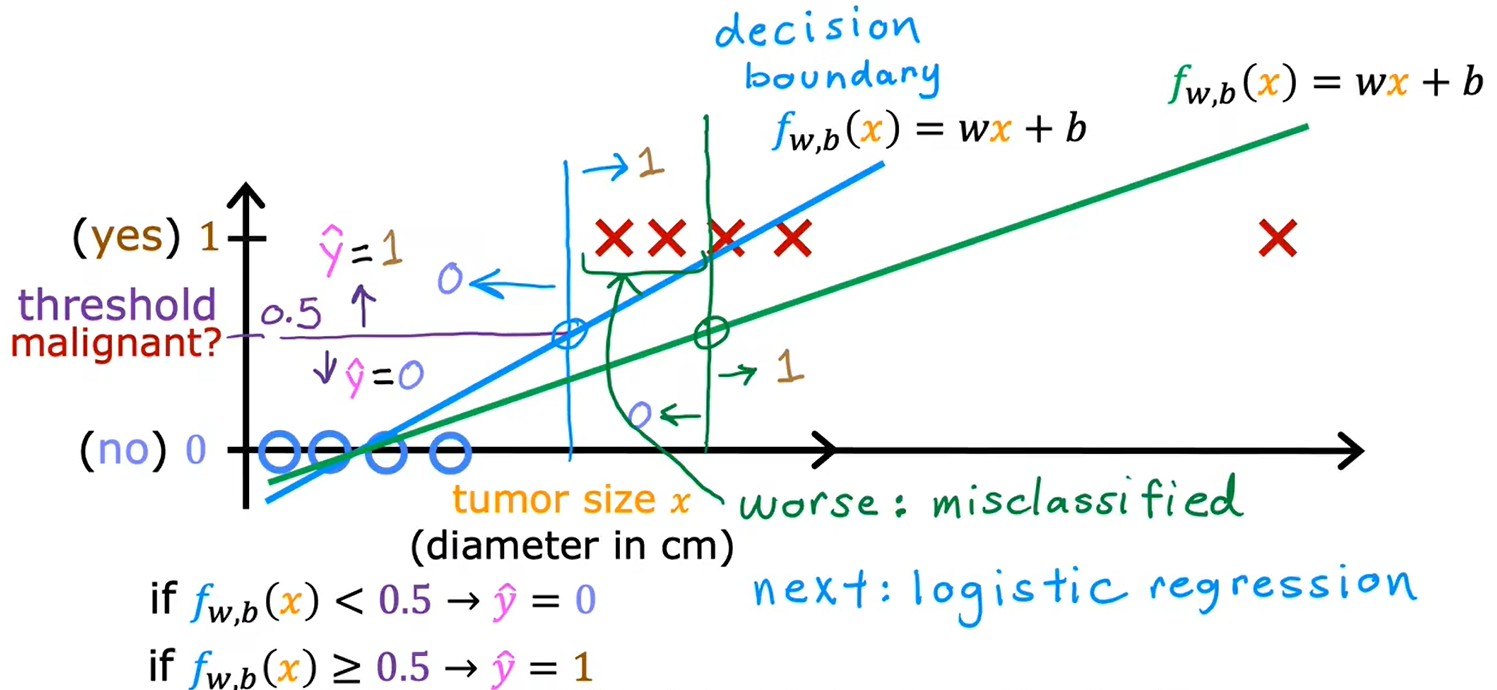
1.2逻辑回归

逻辑回归虽然有“回归”这个词，但它是用来分类的

---

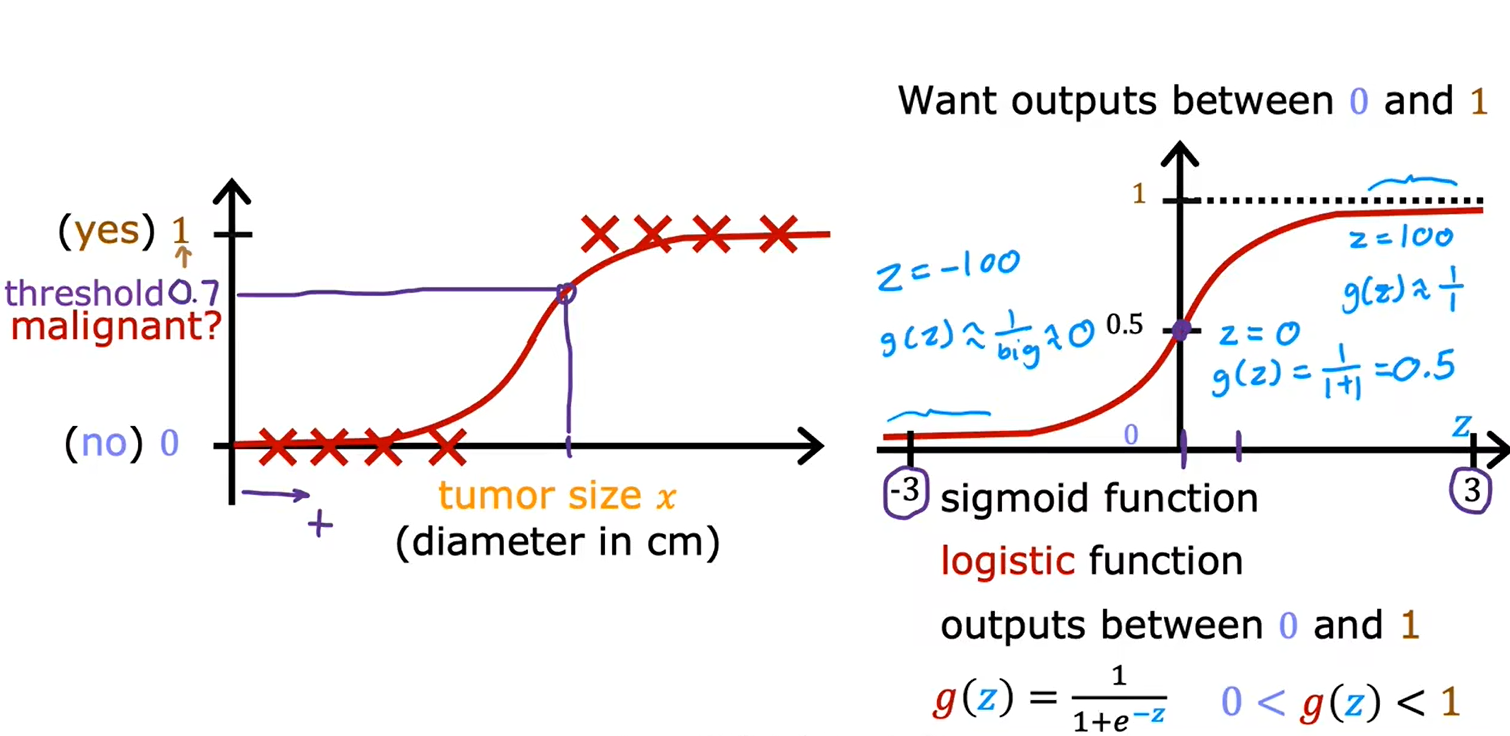
逻辑回归模型

---

---

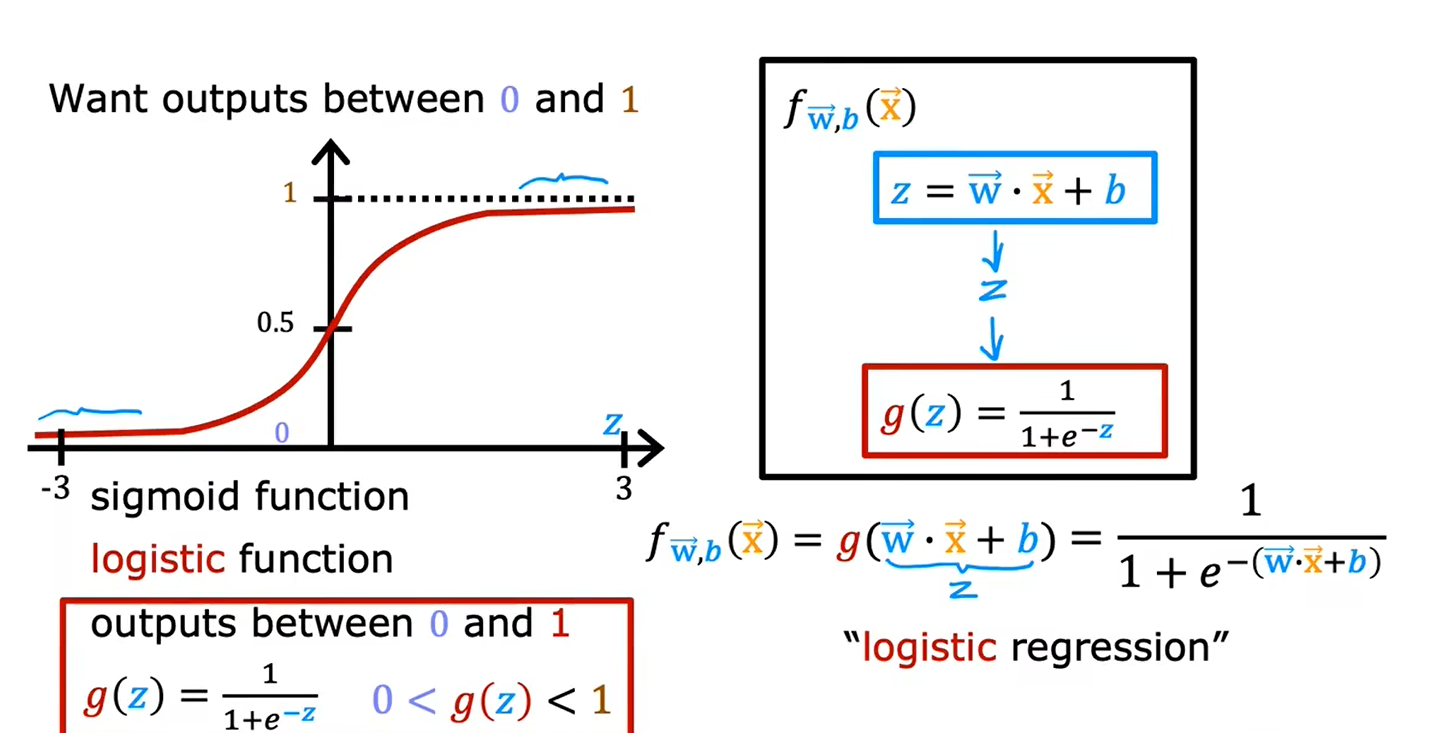
1.3决策边界

---

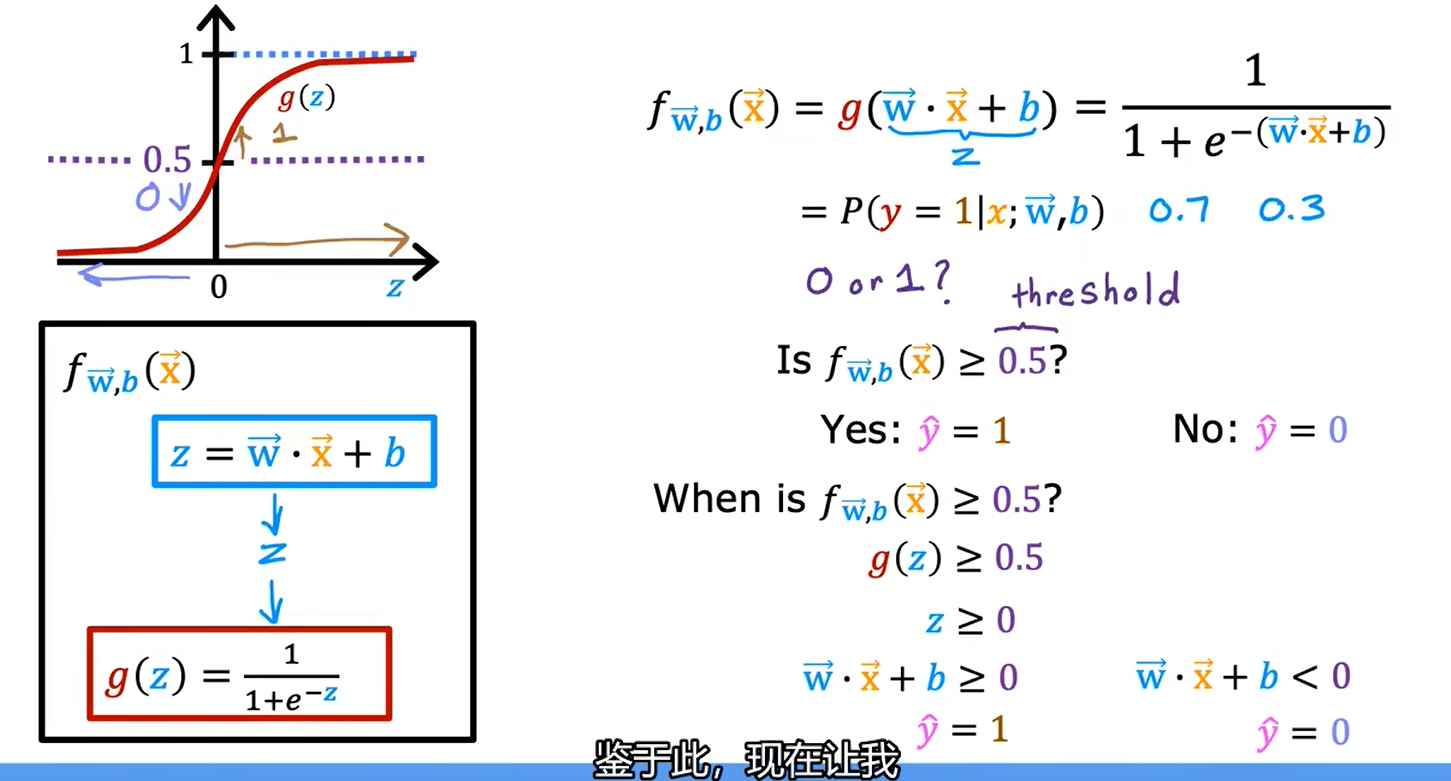
线性决策边界

---

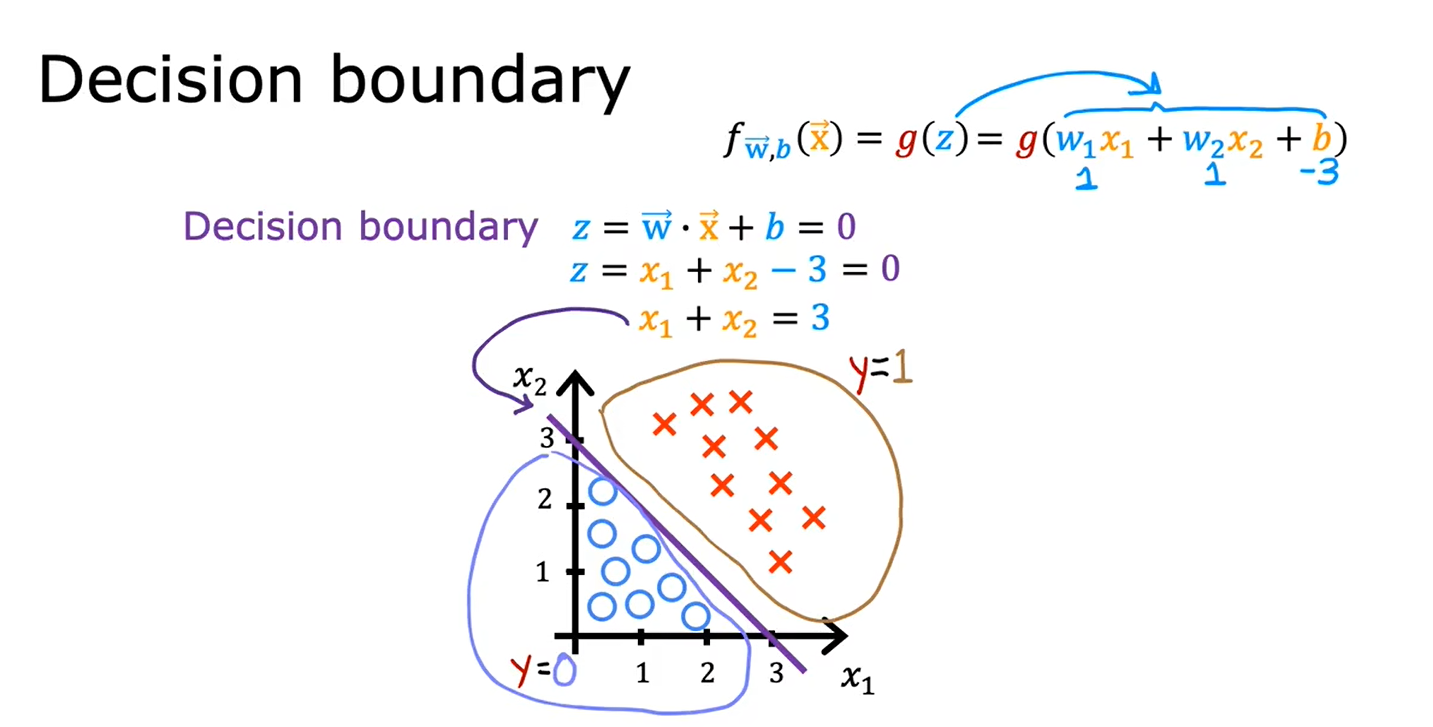
非线性决策边界

---

逻辑回归可以学会拟合非常复杂的数据
如果不用高阶多项式，也就是说你使用的特征只有x1,x2,x3,那么逻辑回归的决策边界永远是线性的，永远是一条直线

---

二、训练逻辑回归模型

2.1逻辑回归中的代价函数

给定训练集，如何选择参数w和b

---

对逻辑回归来说，平方损失函数不是一个好的选择，用它生成的图中会有很多局部最小值

---

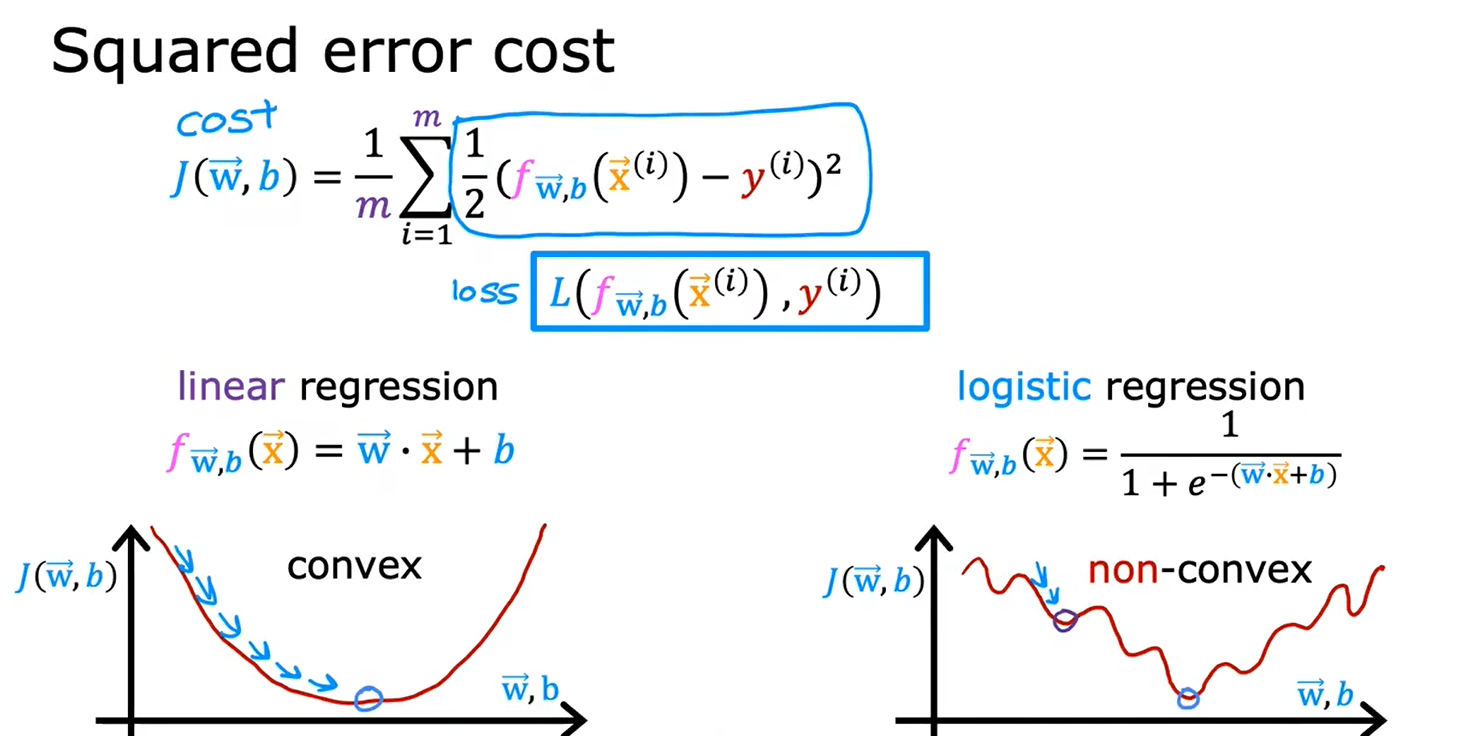
逻辑回归模型定义

---

---

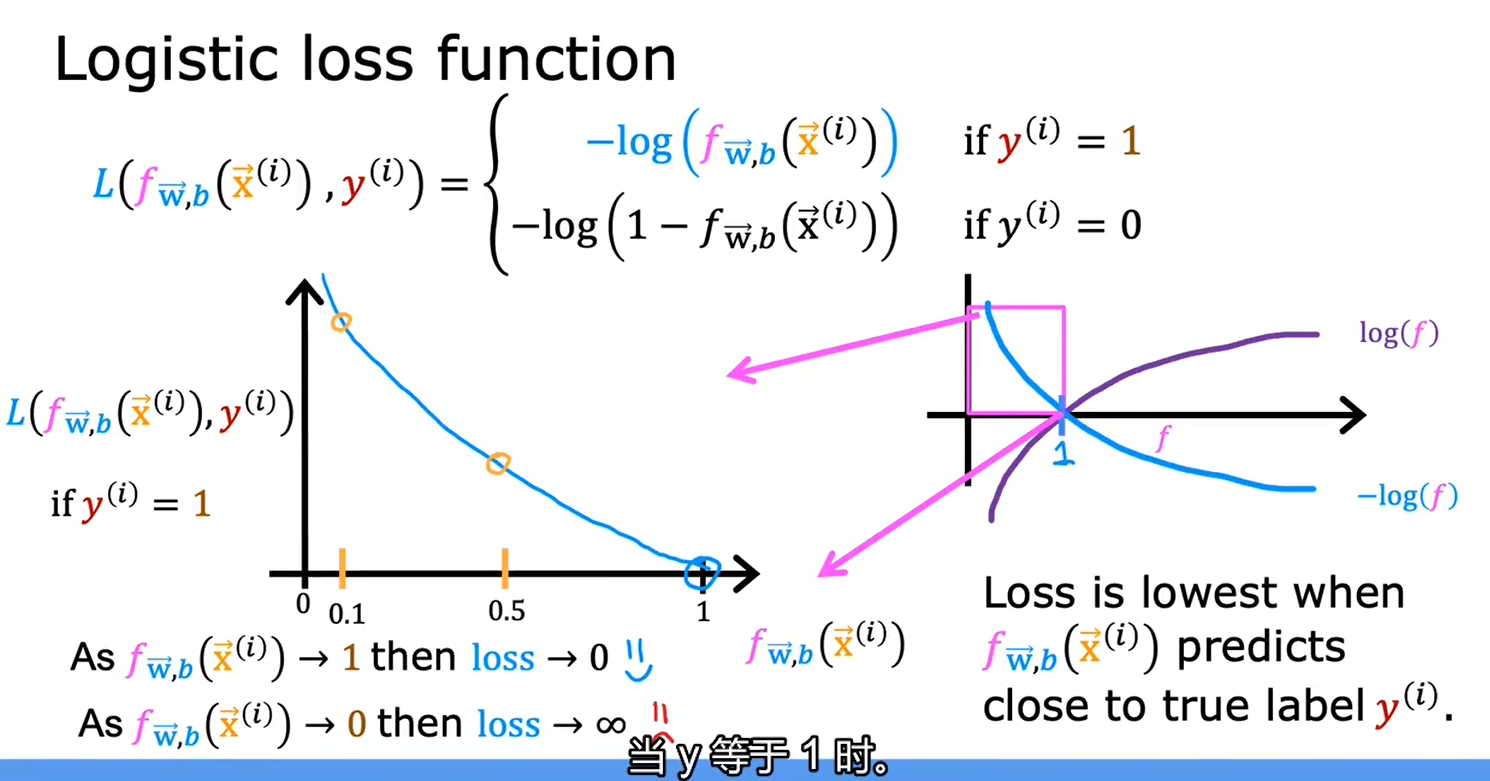
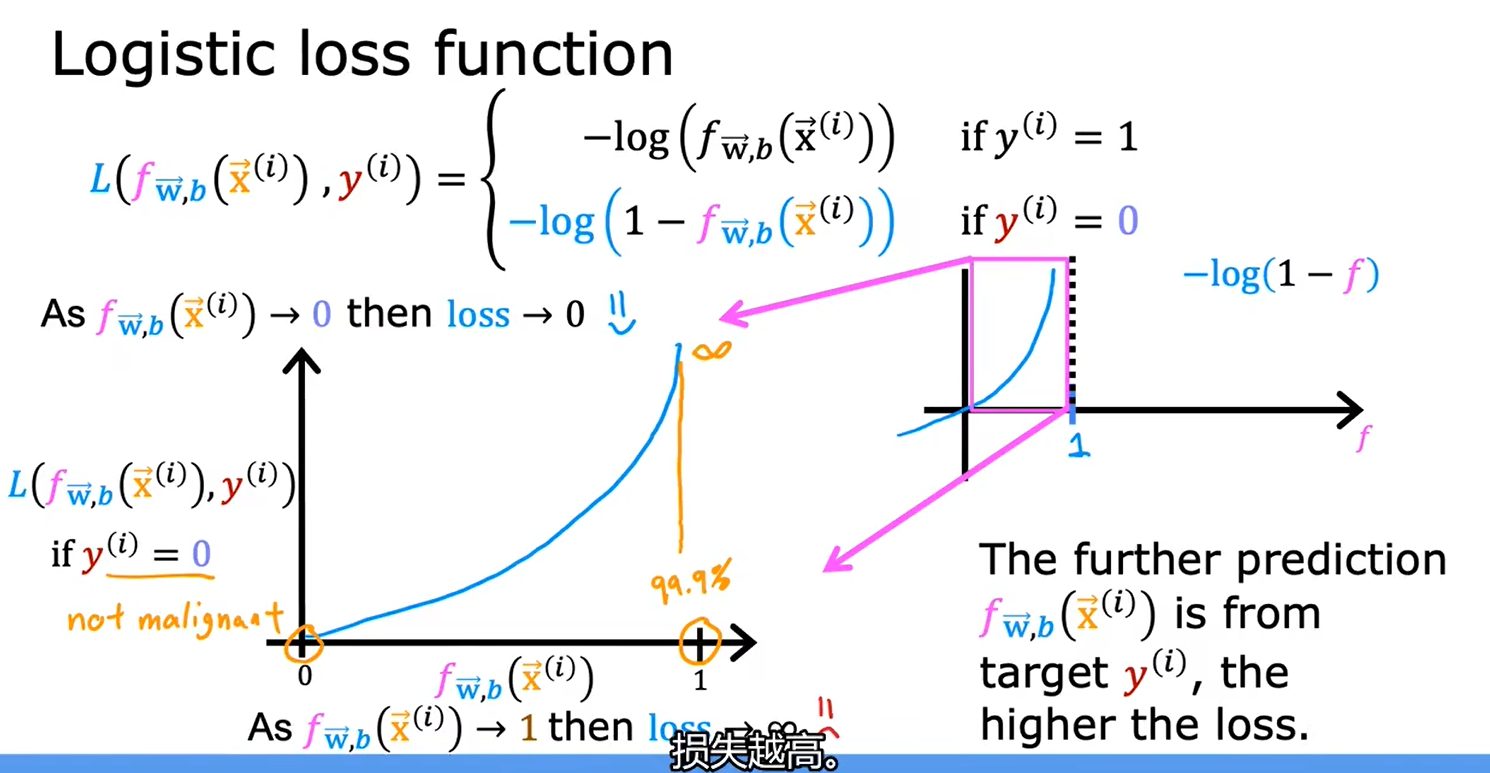
总结

---

2.2简化逻辑回归代价函数

y不是0就是1，不能取其他任何值

---

---

三、逻辑回归中的梯度下降

---

逻辑回归中的梯度下降方法

---

虽然逻辑回归的梯度下降公式和线性回归中的十分相似，但是本质并不一样，因为函数f(x)的定义变了

---

四、正则化

4.1过拟合问题

---

---

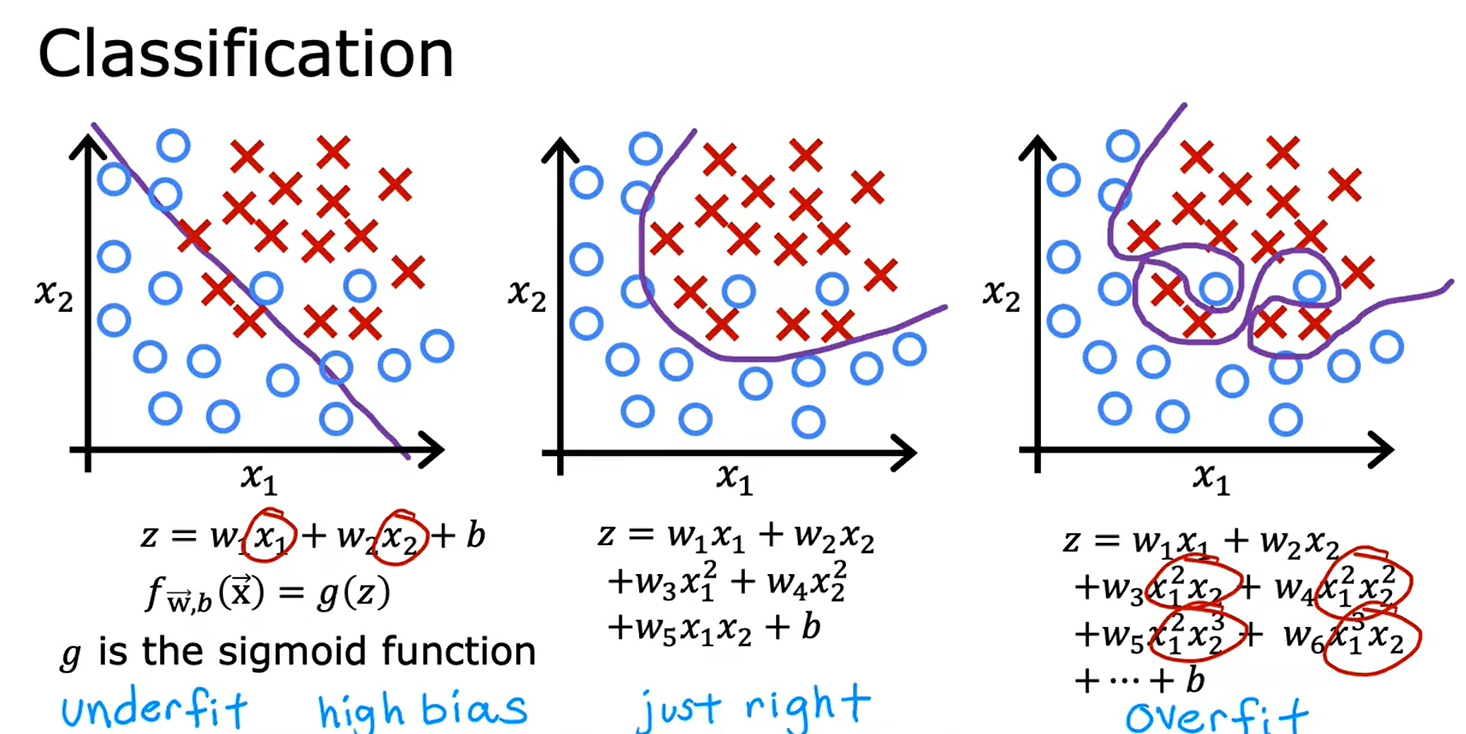
4.2解决过拟合问题

• 收集更多训练数据
• 减少特征数量
• 正则化
  

---

---

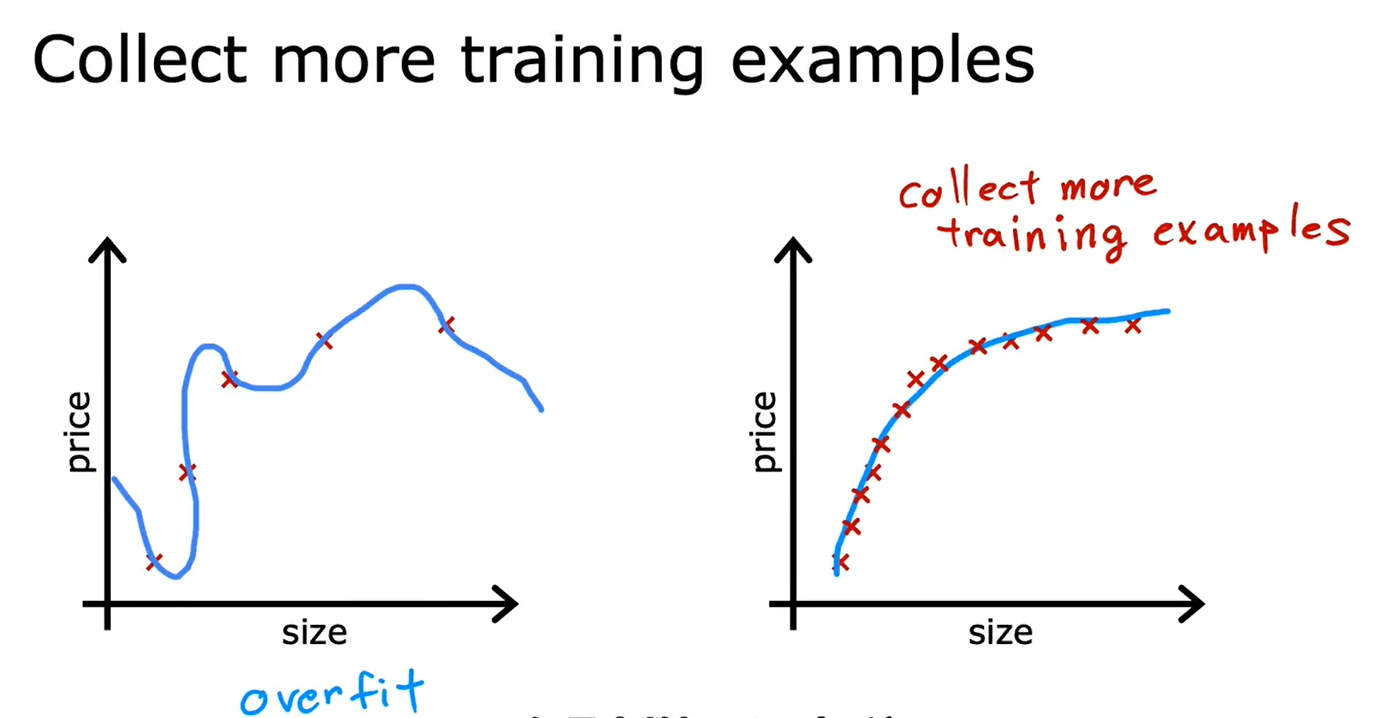
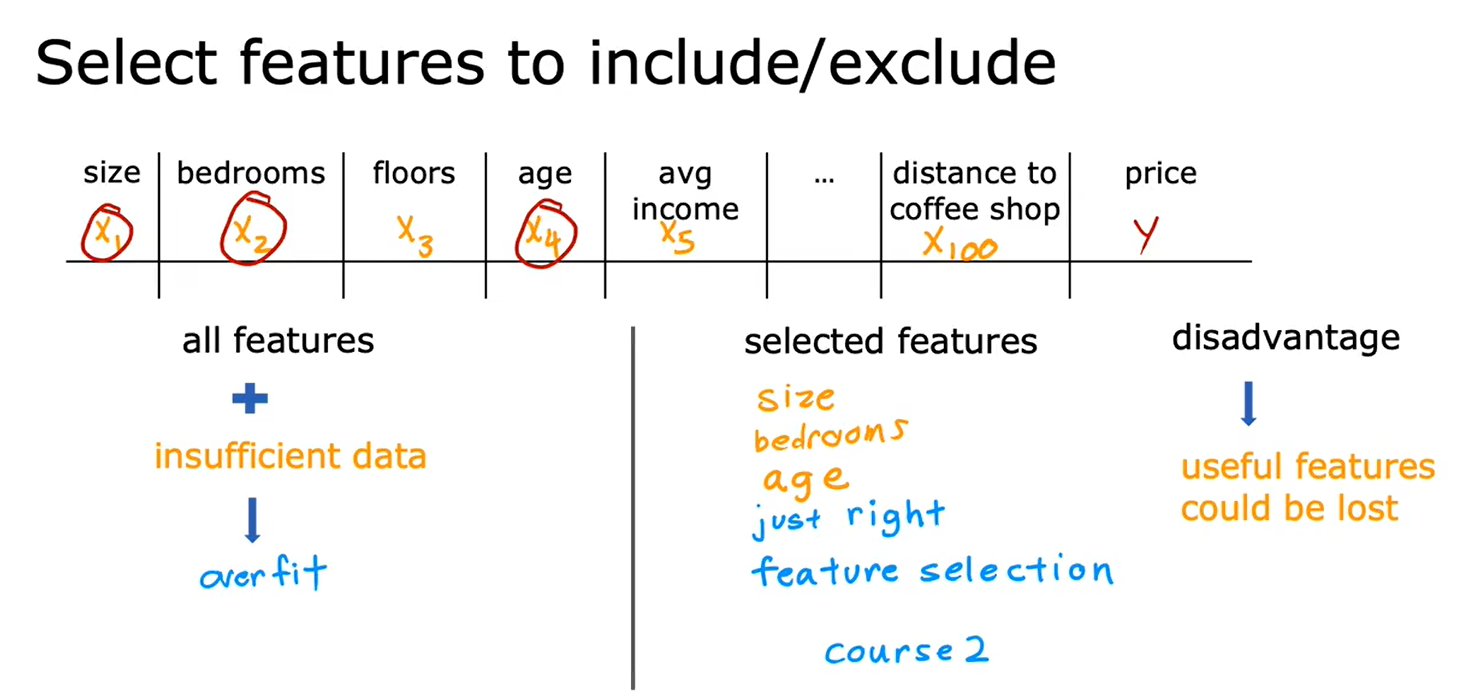
正则化要做的是尽可能地让算法缩小参数的值，而不是要求一定要把参数变为0
正则化的作用是：保留所有的特征，但防止特征权重过大，只有时候会导致过拟合

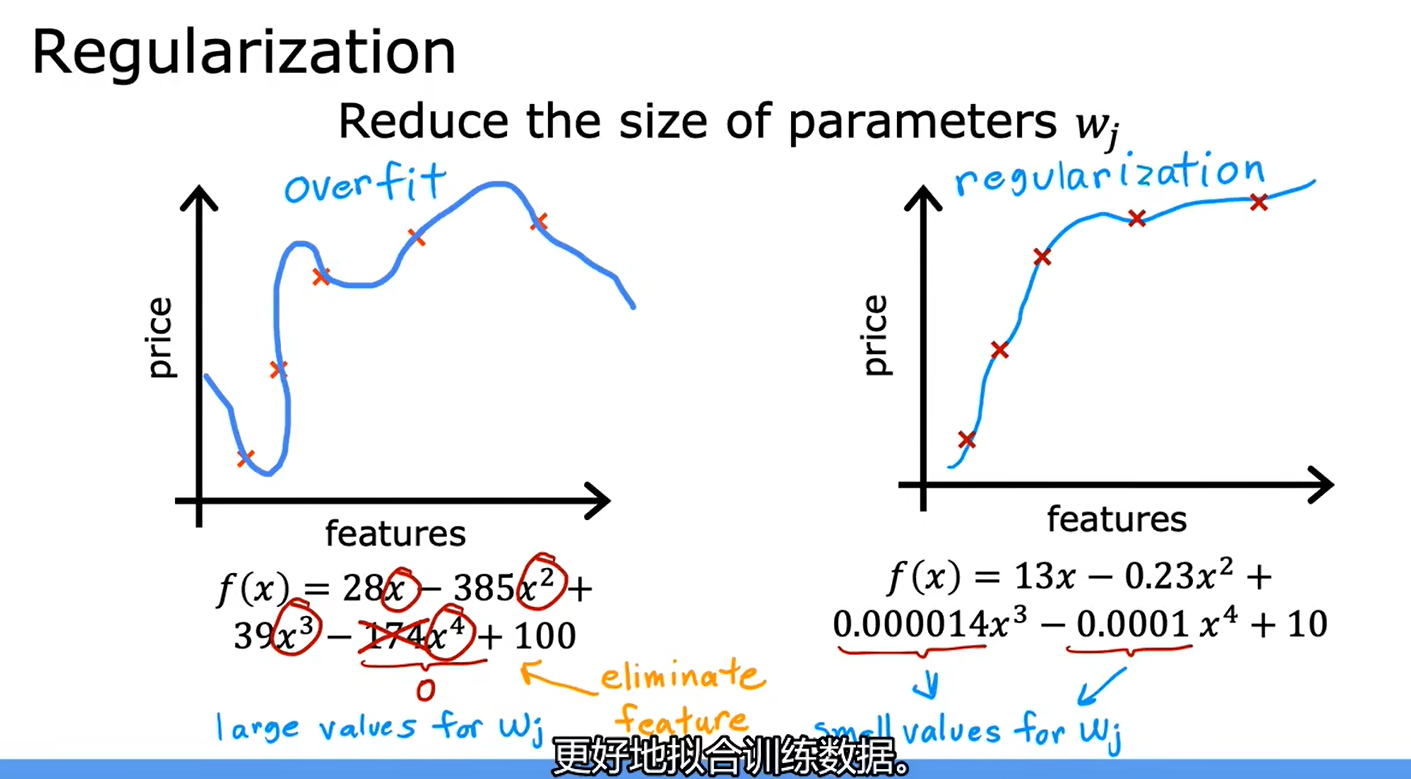
参数b是否正则化，并没有太大的区别

---

总结

---

4.3正则化

---

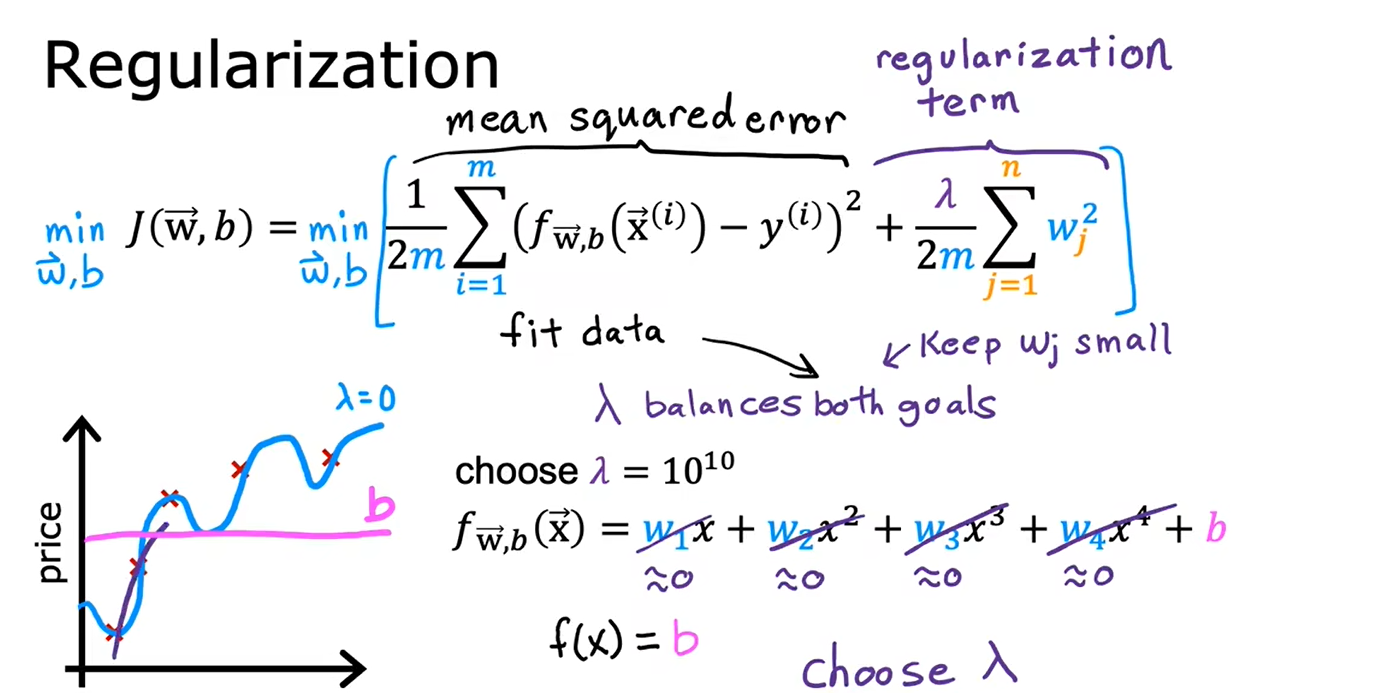
正则化的思想是：参数值越小，模型可能越简单，也许是因为模型的特征变少了，那它过拟合的可能性也变小了

---

选择合适的正则化参数λ

---

4.4用于线性回归的正则化方法

---

以下是可选内容

正则化在每次迭代中做的就是，将w乘上一个略小于1的数

---

推导过程：

---

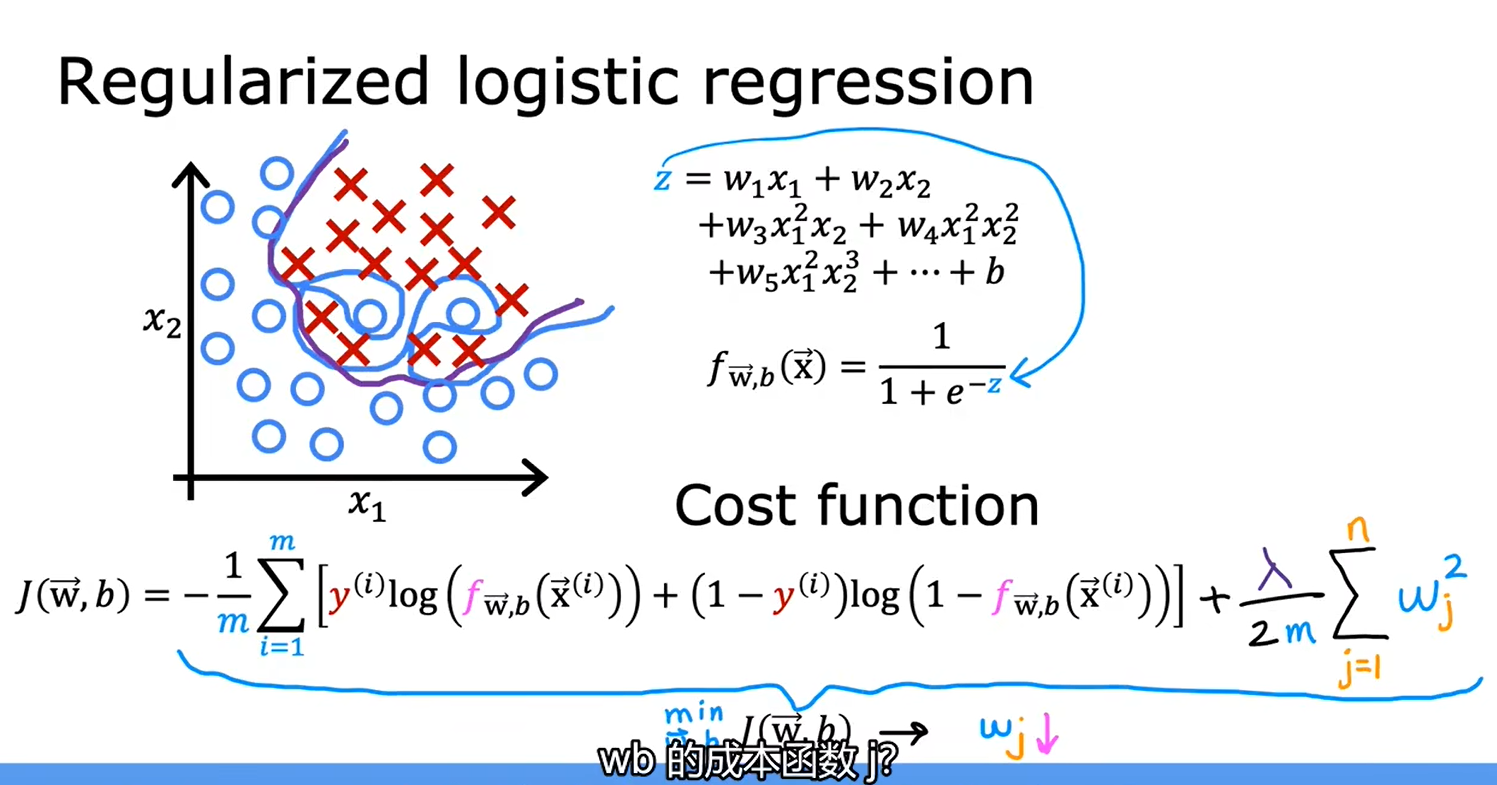
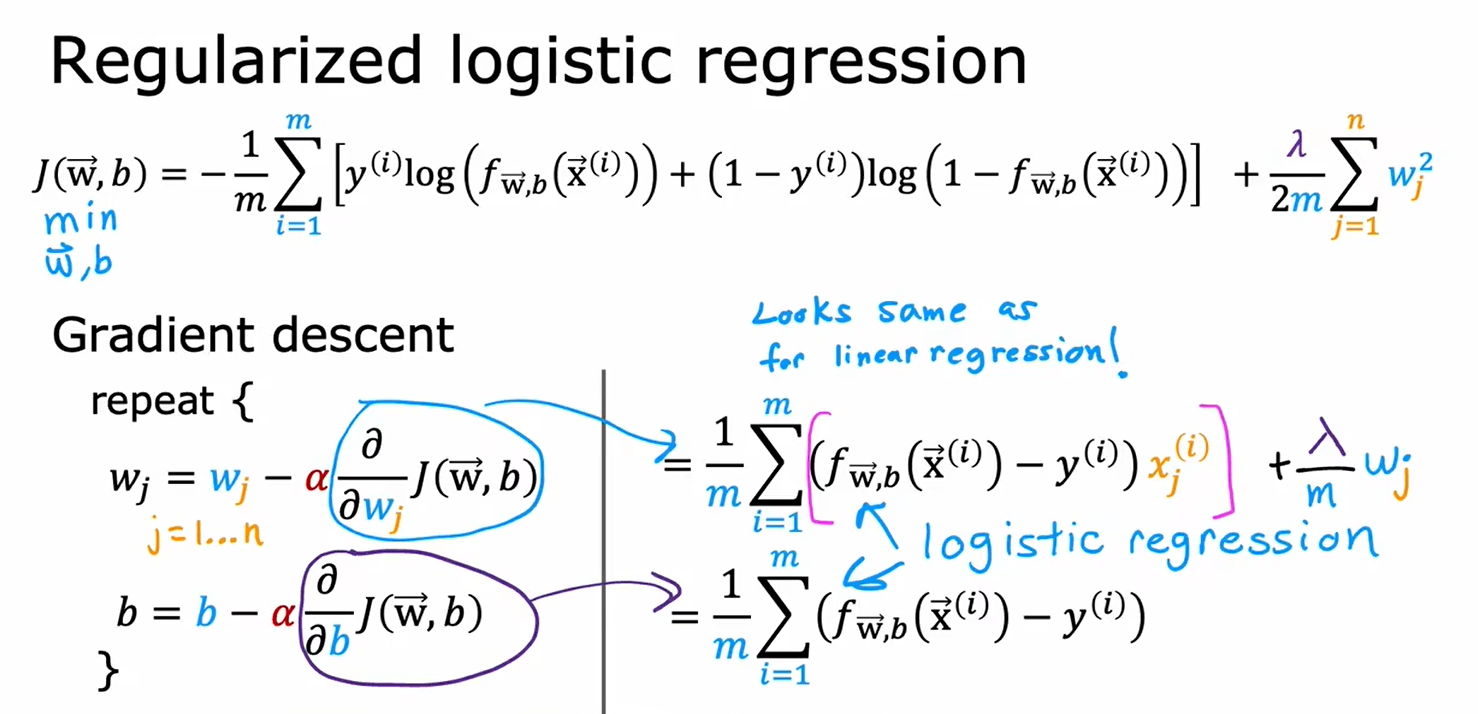
4.5用于逻辑回归的正则化方法

---