本篇复习内容有
求解标准正交基
证明标准正交基
证明正交变换
利用共轭变换证明
求解与给定矩阵的相似矩阵--对角矩阵
1.求标准正交基
在求标准正交基时,通常要先正交化,然后单位化,即可求出标准正交基。


2.证明标准正交基
标准正交基=单位向量组+正交向量组+基
例题:

解法一

解法二
由定理,判断向量组是否为一组基和过渡矩阵是否为正交矩阵即可。


3.证明正交变换
要证明A为正交变换,即证A为线性变换,A为正交变换。(注意是两个条件)
一般的证明思路为下述两个方向:
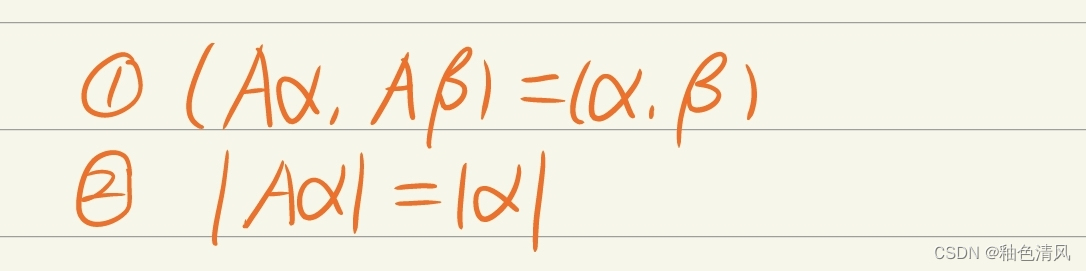
让我们看看经典的证明例题。
例1


例2


例3

首先分析题目:

接下来,我们一步一步证明:



4.利用共轭变换做证明

例1


例2


5.求方阵对应的对角阵
Λ
Λ
Λ以及可逆矩阵P
首先是,最理想的情况,即特征向量的个数等于矩阵的阶数,这是步骤为:

例题1

过程如下:
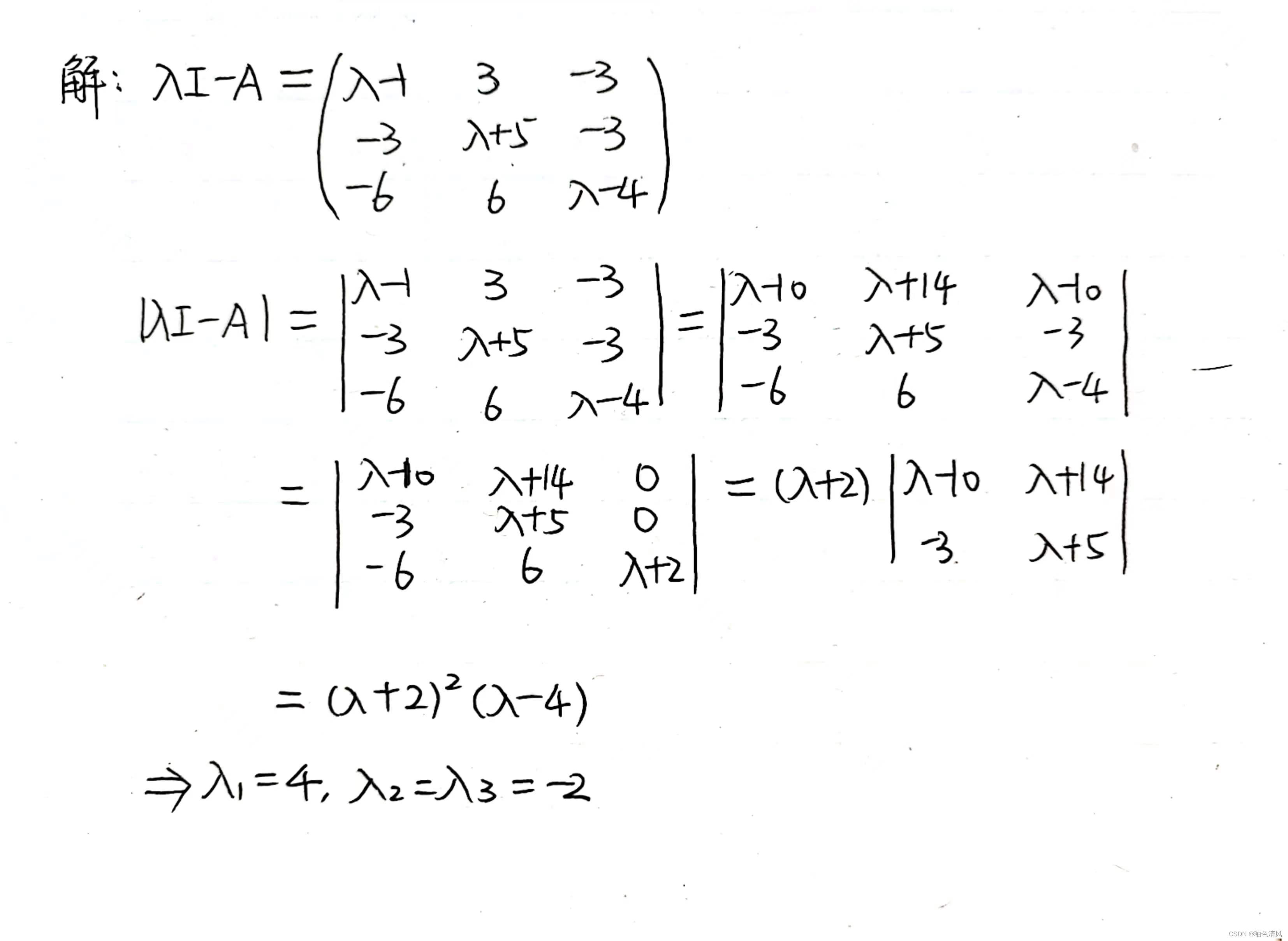
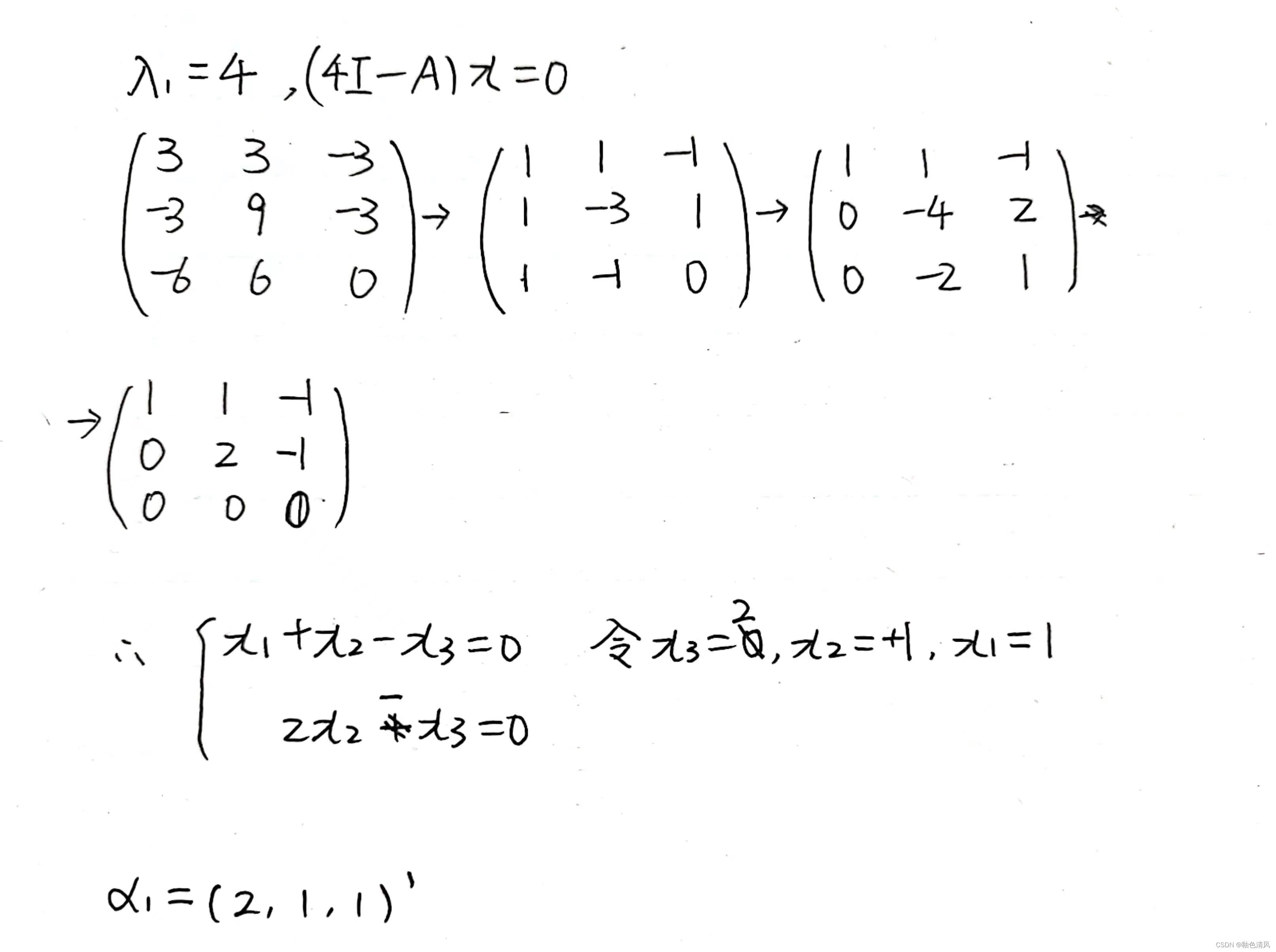
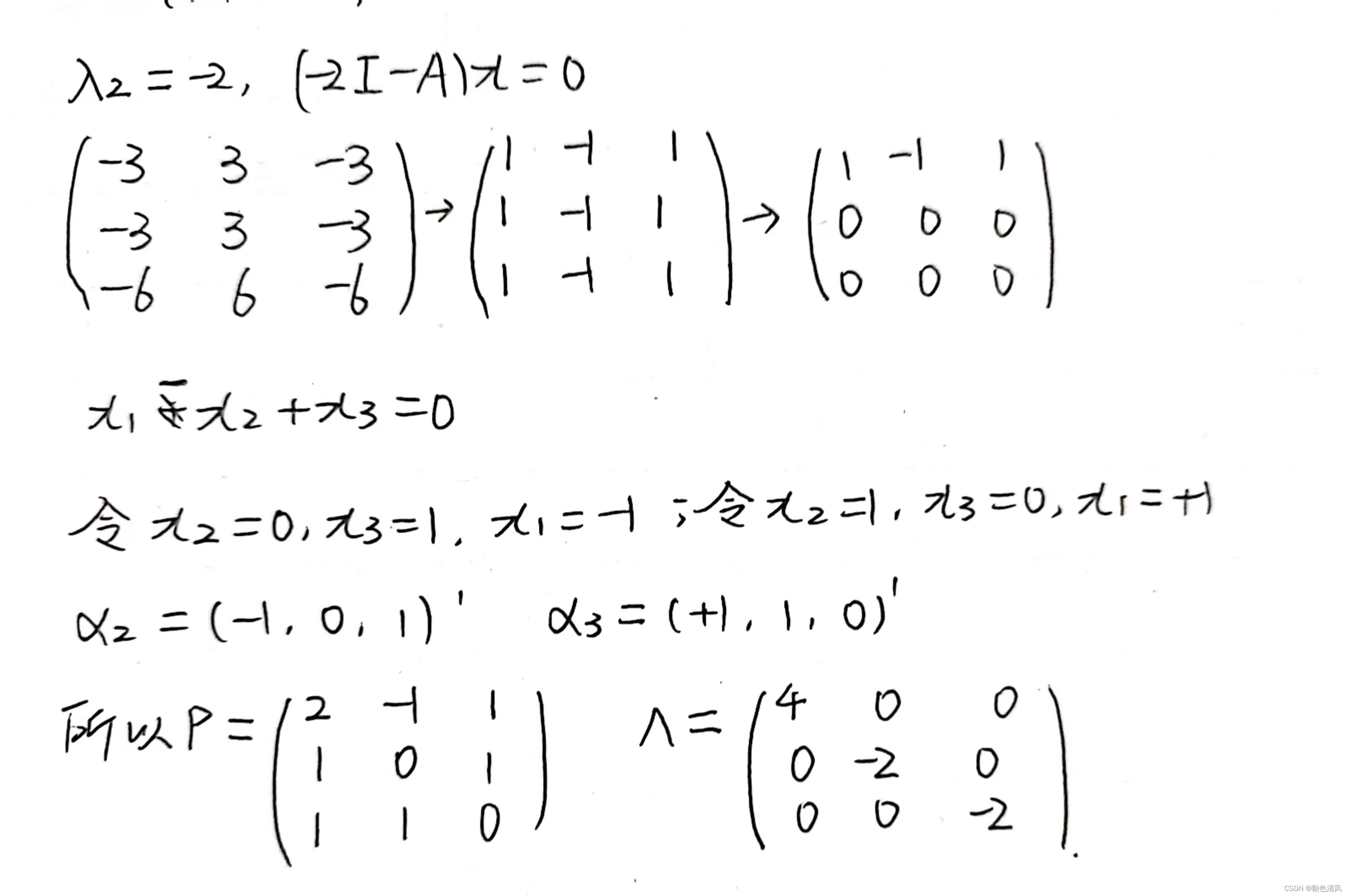
例题2

步骤如下:

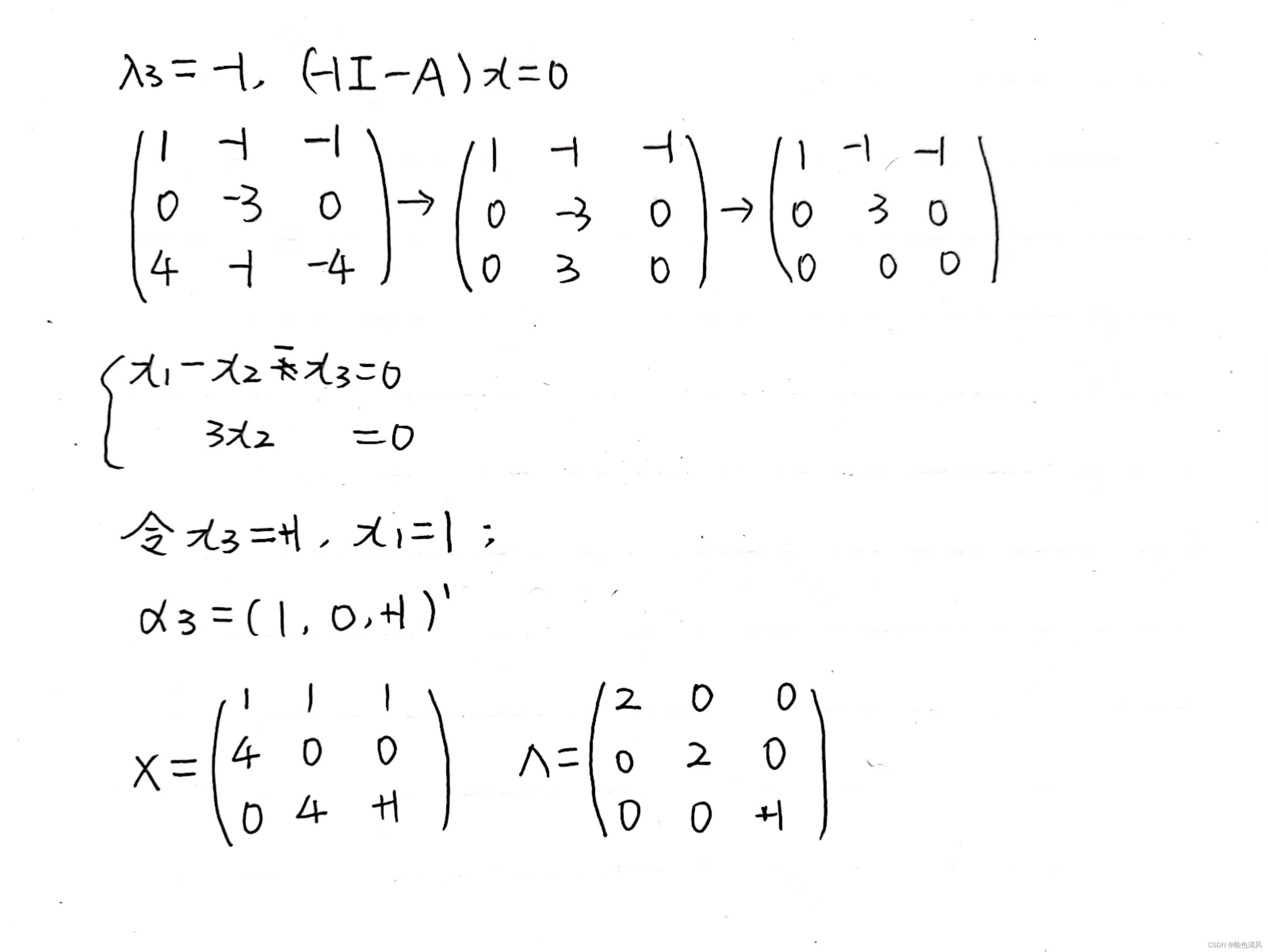
注意!上面的过程是我自己一遍写的,可以看出来,其中的修改之处,都是对过答案之后!好几处都是到了最后的时候化简矩阵数字的正负号给移错,要么对于x1x2x3建立的方程前面的系数抄下来弄错!一定要注意啊!!!