1. 多层感知器

---

感知机（perceptron）早在20世纪50年代就提出来了¹，但直到近几年深度学习的崛起，神经网络才再次走入大众的视野，并且成为了当下最热门的研究方向之一。

一个单层的感知器只能解决线性问题，而要解决如“异或”等非线性问题，则需要引入多层感知器

其原理是通过叠加多个线性的单元，构成非线性的网络

首先考虑一个简单的“与”运算

$$Y=A\&B$$

其真值表如下

A	B	Y	C
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	2

只有当$A$与$B$都为1的时候$Y$才为1，表中$C$为$A$与$B$的数学运算值，即

$$C=A+B$$

将真值表转化为图的形式，其中横坐标$AB$表示$A$和$B$组成的2比特的数。例如：当$A=1$且$B=0$时，$AB=10(二进制)=2(十进制)$

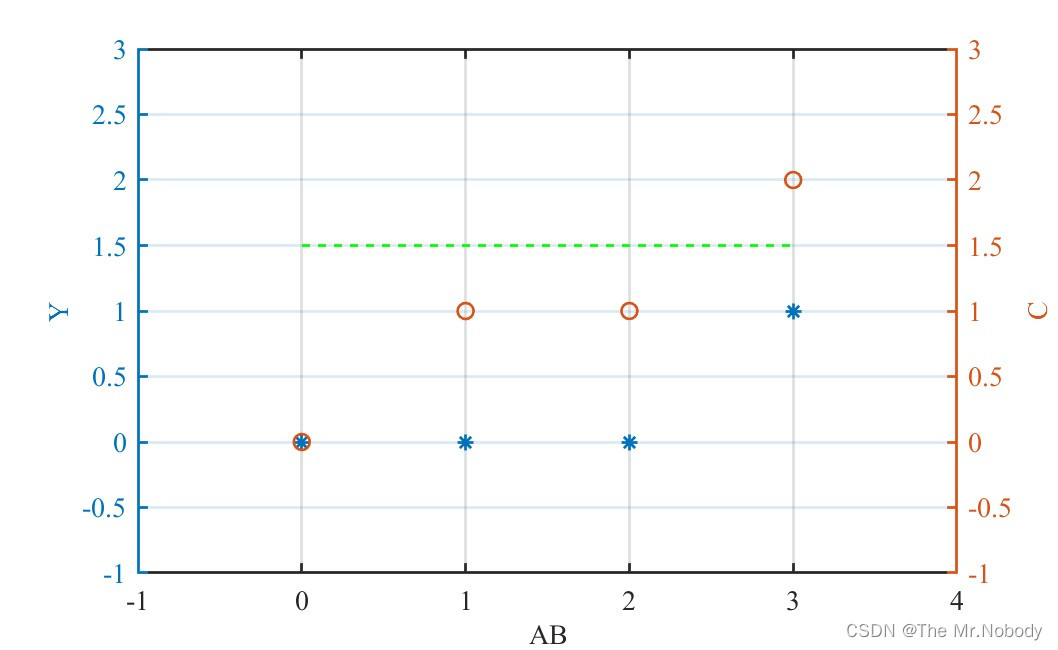
观察$C$的取值与$Y$的关系，可以得到，当$A$与$B$的线性加和大于1.5时，可以认为$A\&B$为1，小于等于1.5时则为0

因此通过引入一个非线性激活函数，可以将数学运算值转化为“与”运算，该运算可以描述为：

$$sgn(A+B-1.5)$$

其中$sgn$表示符号函数

因此一个具有“与”运算功能的神经网络可以表示为

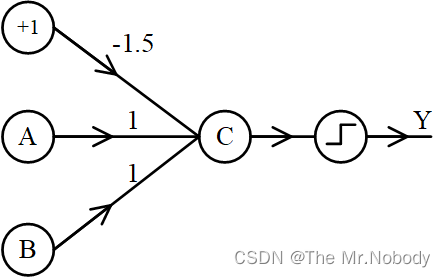
一个“或”运算问题如下

$$Y=A|B$$

通过上述方式可以得到一个具有“或”运算功能的神经网络可以表示为

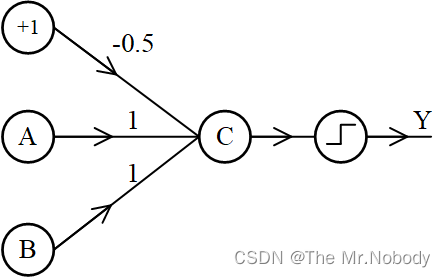
同理可得到具有“非”运算功能的神经元

$$Y=\tilde{A}$$

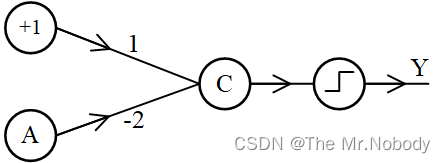
考虑一个“异或”问题：

$$Y=A\oplus B$$

这是一个非线性对应关系，无法用一个简单的神经元表示

但是从逻辑上分析，一个“异或”问题可以转化为“与”和“或”问题的组合，即

$$Y=A\oplus B=(A|B)\&(\tilde{A}|\tilde{B})$$

则其对应的神经网络可以表示为

检验一下真值表

A	B	Y	C1	C2	C	Y
0	0	0	-0.5	1.5	-0.5	0
0	1	1	0.5	0.5	0.5	1
1	0	1	0.5	0.5	0.5	1
1	1	0	1.5	-0.5	-0.5	0

可以看到多层感知器可以解决“异或”问题

2. BP算法

---

待续

参考文献

---

1. Rosenblatt, F., 1958. The perceptron: a probabilistic model for information storage and organization in the brain. Psychological review, 65(6), p.386. ↩︎