全文目录
机器学习技术的实施方法
预测阶段效果监控
离线预测+在线预测
-
监控点击率的稳定性
- 真实点击率的稳定性
计算相邻两个区间内点击率分布的 PSI(Population Stability Index, 群体稳定性指标), 小于 0.1 可认为数据相对稳定; - 预测点击率的稳定性
与系统本身和用户发生变化有关; - 预测点击率和真实点击率差异的稳定性
- 真实点击率的稳定性
-
监控预测AUC的稳定性
考虑展现偏差; -
监控特征覆盖的稳定性
- 衡量一条样本取值不为零的特征的平均数量;
- 对于一个特征或一组特征能够覆盖的样本数量;
模型训练系统架构设计
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-koERfDaR-1687077499412)(assets/20210304083025.png)]](https://img-blog.csdnimg.cn/0124a97396c94fe2a41ac2f6fe27cf59.png)
特征生成器 = 一组配置数据 + 一组解析程序;
典型: 根据用户的 key 和物品的 key 到原始特征库中获取所需要的原始特征, 然后按照配置的要求进行处理, 得到最终可用的特征;
特征生成器:
- 配置数据的生成
- 通过规则指定;
- 维度过高且需要逻辑计算, 需要通过代码计算拟合;
- 解析程序的生成
- Spark MLlib 中的算子, 转换器;
特征生成器的好处:
- 预测流程中也可以使用同一套特征生成器, 最大程度保证训练阶段和预测阶段特性的一致性;
- 只依赖原始特征, 复杂的特征工程处理封装在逻辑中;
- 基于"算子复用+配置开发"的特征开发方式;
模型预测系统架构设计

常用模型介绍
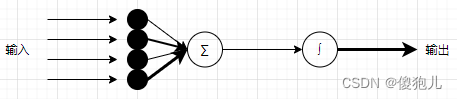
逻辑回归(LR)模型
Logistic Regression, LR
y
=
f
(
x
)
=
1
1
+
e
−
z
,
z
=
∑
i
w
i
×
x
i
y = f(x) = \frac{1}{1+e^{-z}}, z = \sum_i{w_i \times x_i}
y=f(x)=1+e−z1,z=i∑wi×xi
线性部分(z)+logistic部分;
y 表示一个物品被用户点击的概率, 1-y 即用户不点击该物品的概率;
o
d
d
s
=
y
/
(
1
−
y
)
odds = y/(1-y)
odds=y/(1−y), 一件事情发生与不发生的的比例;
l
o
g
y
1
−
y
=
l
o
g
1
e
−
z
=
l
o
g
e
z
=
z
log\frac{y}{1-y} = log\frac{1}{e^{-z}} = loge^z = z
log1−yy=loge−z1=logez=z
LR 模型将 log-odds 统计量建模为线性问题;
优点:
- logistic 函数与交叉熵损失函数搭配使用, 在使用基于梯度的方法时梯度消失的概率较小, 有利于模型的优化;
- 变量之间的线性组合=>较好可解释性;
- 将变量全部转为离散的0-1变量, 预测阶段变的简单;
- logistic 函数输出 0-1 的光滑函数, 符合概率密度函数定义, 结果是高度校准的, 方便模型后续的其他接入;
缺点:
- 所有特征之间均为线性关系, 不支持非线性能力;
- 模型效果的提升大量依赖特征工程(工作量较大);
优先尝试的模型
GBDT模型
Gradient Boosting Decision Tree, 梯度提升树 = 梯度方法(gradient) + boosting + 决策树(decision tree);
- 决策树, 核心, if-else 条件实现特征的非线性组合;
- boosting, 实现多棵树, 后者修正前者的误差, 不断减少模型的偏差, 提升精度的效果; 于此相对的 随机森林 是通过 bagging 的方法实现树的组合;
- 基于梯度作为损失函数, 应用更广;
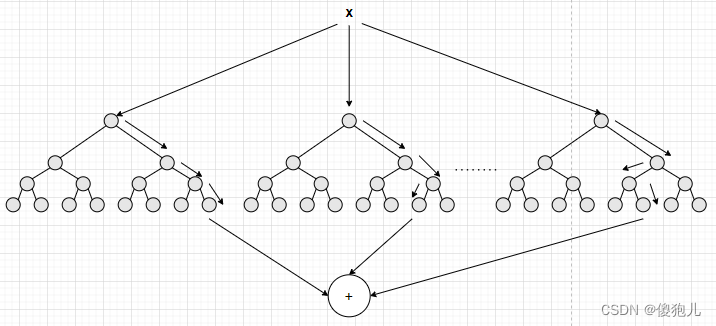
优点:
- 自动特征组合, 引入非线性能力;
- 对数据容纳性好, 对数值特征不需要做分桶离散化处理; 对数值特征异常值不需要特殊处理; 对离散型变量也可以处理;
缺点: - 自动组合的特征含义不够明确, 可解释性差;
- 特征的重要性无法直接度量;
- boosting 组合方法的特点决定了树与树之间只能串行训练, 限制模型训练的并行度;
LR+GBDT模型
facebook 2014年提出;
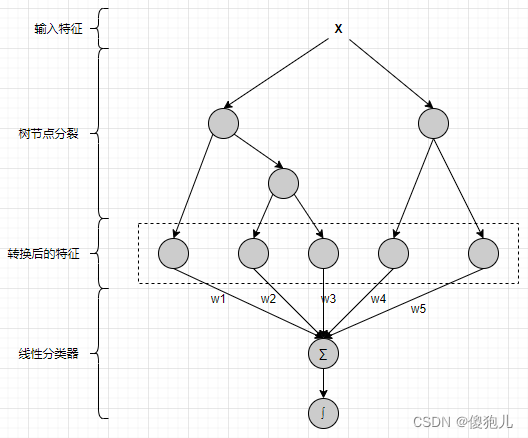
流程:
- 训练数据划分A, B组;
- A组数据训练 GBDT 模型;
- B组训练数据, 每条样本走一遍训练好的 GBDT 模型, 在每棵树中走到的叶子节点作为一个 ID 类特征;
- 将 B 组数据中的 LR 模型特征和上一步生成的叶子节点特征合并, 训练最终的 LR 模型;
区分A, B组数据, 是不希望参与树模型训练的数据再参与 LR 模型的训练, 造成过拟合;
因子分解机模型
Factorization Machine, FM
y
=
f
(
x
)
=
w
0
+
∑
i
=
1
n
w
i
x
i
+
∑
i
=
1
n
∑
j
=
i
+
1
n
<
v
i
,
v
j
>
x
i
x
j
y = f(x) = w_0 + \sum_{i=1}^n w_ix_i + \sum_{i=1}^n\sum_{j=i+1}^n <v_i, v_j>x_ix_j
y=f(x)=w0+i=1∑nwixi+i=1∑nj=i+1∑n<vi,vj>xixj
- w 0 w_0 w0 偏差部分;
- ∑ i = 1 n w i x i \sum_{i=1}^n w_ix_i ∑i=1nwixi 线性部分, 与 LR 模型中 z z z 的计算方式相同;
-
∑
i
=
1
n
∑
j
=
i
+
1
n
<
v
i
,
v
j
>
x
i
x
j
\sum_{i=1}^n\sum_{j=i+1}^n<v_i,v_j>x_ix_j
∑i=1n∑j=i+1n<vi,vj>xixj 非线性部分, 增加模型描述能力; 所有特征两两组合形成组合特征, 两个向量的内积结果作为权重;
每个组合特征是由两个 k 维向量 v 计算内积得到的, 即 n 个 x 的 v 向量组成了全部的组合特征的参数, 数量是 nk 个, O(nk) 量级;
M = V V T M = VV^T M=VVT - M i , j M_{i,j} Mi,j 特征 x i x j x_ix_j xixj 对应参数
- V i V_i Vi 为 FM 模型中的向量参数 v i v_i vi
优点:
- 自动构造全量组合特征, 节省人工工作量, 实现全量线性+非线性+向量力度的特征表达;
- 引入矩阵分解将参数量降维, 增加组合特征参数的训练样本量, 降低训练难度, 提升训练效果;
Wide & Deep 模型
与 FM 模型的区别: 使用深度神经网络构造非线性特征;
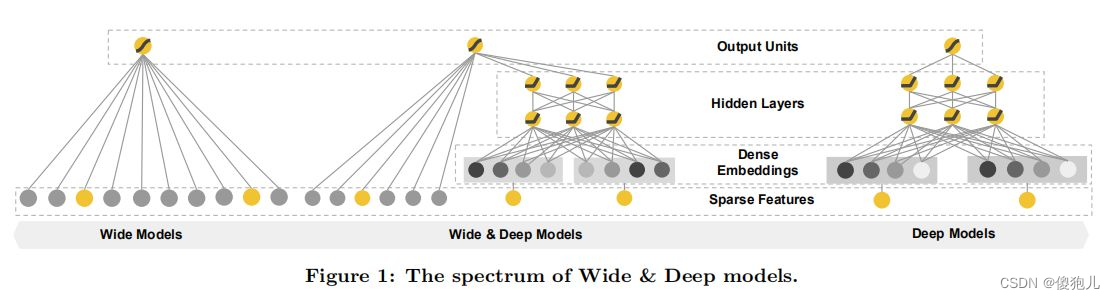
- wide 部分负责记忆, 解决用户没有行为的物品或标签在预测数据中出现从而导致无法判断用户和物品相关性信息的问题; 将用户和物品的特征输入到一个神经网络中, 学习出这些特征的向量化表示;
- deep 部分主要是离散特征, embedding 编码后输入神经网络中; 把同一批离散特征分别用作线性特征和深度特征, 同时实现记忆和泛化功能(特征交叉转换);

其他深度学习模型
DIN, DCN, PNN, DeepFM等
知其然, 知其所以然;
提出模型的原因, 与其他模型的关系;
机器学习实践常见问题
反模式:
-
只见模型, 不见系统;
以系统全局观看到问题, 模型优化服务目标是最终是为了调优系统; -
忽视模型过程和细节;
LR 模型适合用于排查模型内部异常参数; 把控训练过程细节来把控最终模型; -
不注重样本精细化处理;
对负样本的界定不够细致; 对样本概念的理解不到位; -
过于依赖算法;
-
核心数据缺乏控制;
用数据的人保证对数据的控制性; -
团队不够全栈;
关注整个系统的全局性思维; -
系统边界模糊导致出现"巨型系统";
巨型系统特点:- 模块间不可拆分, 样本, 特征, 训练等步骤都耦合在一起;
- 实验性, 探索性代码遍布其中, 分不清;
- 模型整体流程(pipeline)特别长, 部分已经无用的流程;
-
不重视基础数据架构建设;
样本数据, 原始特征数据, 处理后的特征数据, 支撑数据等;
保证数据的可用性和可探索性;
本文仅作为读书笔记使用!