1、题目

2718. 查询后矩阵的和 - 力扣（Leetcode）

给你一个整数 n 和一个下标从 0 开始的 二维数组 queries ，其中 queries[i] = [typei, indexi, vali] 。

一开始，给你一个下标从 0 开始的 n x n 矩阵，所有元素均为 0 。每一个查询，你需要执行以下操作之一：

如果 typei == 0 ，将第 indexi 行的元素全部修改为 vali ，覆盖任何之前的值。
如果 typei == 1 ，将第 indexi 列的元素全部修改为 vali ，覆盖任何之前的值。

请你执行完所有查询以后，返回矩阵中所有整数的和。

示例 1：

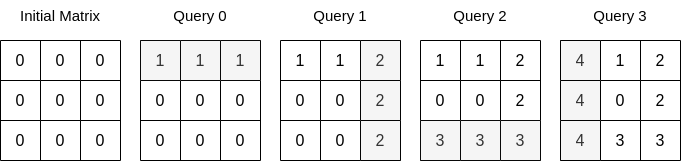
输入：n = 3, queries = [[0,0,1],[1,2,2],[0,2,3],[1,0,4]]
输出：23
解释：上图展示了每个查询以后矩阵的值。所有操作执行完以后，矩阵元素之和为 23 。

示例 2：

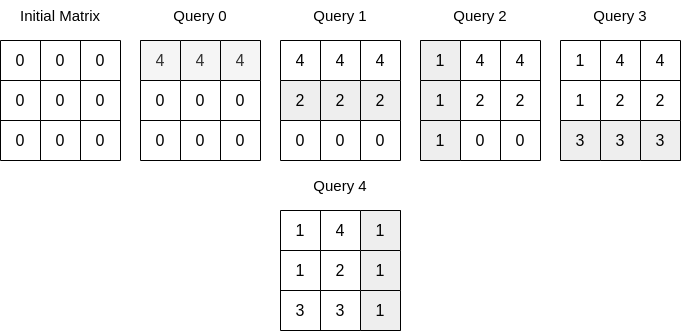
输入：n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]]
输出：17
解释：上图展示了每一个查询操作之后的矩阵。所有操作执行完以后，矩阵元素之和为 17 。

提示：

1 <= n <= 104
1 <= queries.length <= 5 * 104
queries[i].length == 3
0 <= typei <= 1
0 <= indexi < n
0 <= vali <= 105

2、题目解读

题目要求我们通过 queries 数组的值进行操作，去改变 n*n矩阵，最后计算矩阵元素之和。

queries[i] = [typei, indexi, vali]

遍历 queries数组：

如果 typei == 0 ，将第 indexi 行的元素全部修改为 vali ，覆盖任何之前的值。
如果 typei == 1 ，将第 indexi 列的元素全部修改为 vali ，覆盖任何之前的值。

我们可以进行queries数组倒序遍历，去进行修改矩阵，因为最先修改的操作可能是无用的操作，会被后面的操作覆盖，而最后面的操作基本上就不会被覆盖了。

示例1倒序过程：

在倒序时，如果发现矩阵某位置已经被改变（怎么判断它已经被改变？如果修改的数就是0呢？）就不用修改该位置的值。

示例2倒序过程：

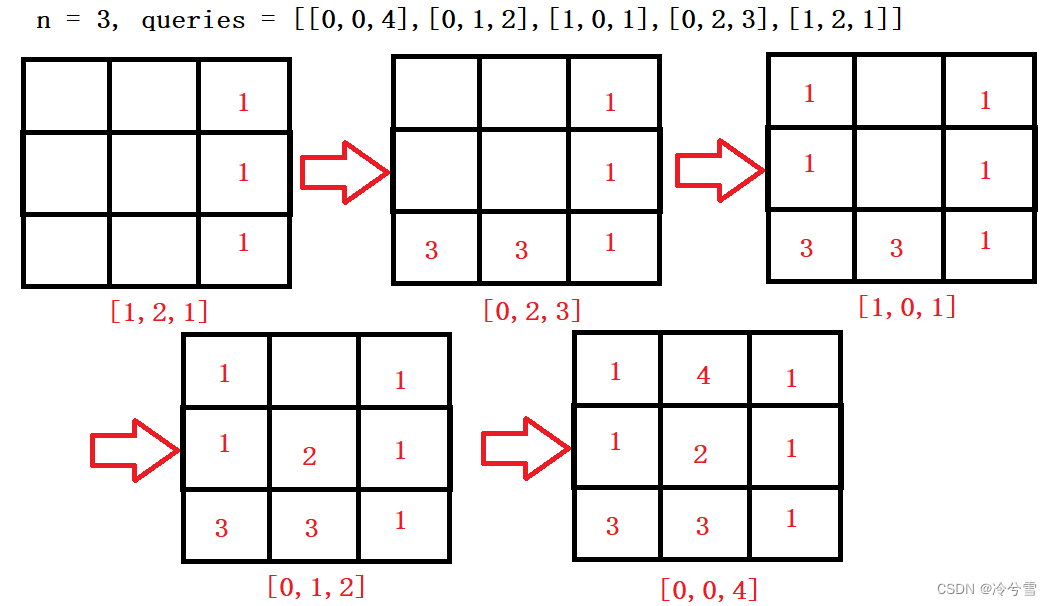
上面提到使用什么来怎么判断它已经被改变？我们可以使用Set去判断记录标记是否已经修改，然后再进行是否需要更改。

然后直接计算矩阵和 +n - vis_col.size()*vali

3、代码

java：

class Solution {
    public long matrixSumQueries(int n, int[][] queries) {
        long ans = 0;
        Set<Integer> vis_row = new HashSet<>();
        Set<Integer> vis_col = new HashSet<>();
        for (int i = queries.length - 1; i >= 0; i--) {
            int type = queries[i][0], index = queries[i][1], val = queries[i][2];
            if (type==0){
                if (!vis_row.contains(index)){
                    ans+= (long) (n - vis_col.size()) *val;
                    vis_row.add(index);
                }
            }else {
                if (!vis_col.contains(index)){
                    ans+= (long) (n - vis_row.size()) *val;
                    vis_col.add(index);
                }
            }
        }
        return ans;
    }
}

可能这样写不好看

class Solution {
     public long matrixSumQueries(int n, int[][] queries) {
        long ans = 0;
        Set<Integer>[] vis = new Set[]{new HashSet<>(), new HashSet<>()};
        for (int i = queries.length - 1; i >= 0; i--) {
            int type = queries[i][0], index = queries[i][1], val = queries[i][2];
            if(vis[0].size()==n&&vis[1].size()==n)
                break;
            if (!vis[type].contains(index)) { // 后面（>i）没有对这一行/列的操作
                // 这一行/列还剩下 n-vis[type^1].size() 个可以填入的格子
                ans += (long) (n - vis[type ^ 1].size()) * val;
                vis[type].add(index);
            }
        }
        return ans;
    }
}

Python：

class Solution:
    def matrixSumQueries(self, n: int, queries: List[List[int]]) -> int:
        ans = 0
        vis_row = set()
        vis_col = set()
        for tp, index, val in reversed(queries):
            if tp == 0:
                if index not in vis_row:
                    ans += (n - len(vis_col)) * val
                    vis_row.add(index)
            else:
                if index not in vis_col:
                    ans += (n - len(vis_row)) * val
                    vis_col.add(index)
        return ans

可能这样写不好看

class Solution:
    def matrixSumQueries(self, n: int, queries: List[List[int]]) -> int:
        ans = 0
        vis = [set(), set()]
        # 使用reserve方法不会有额外的空间开销
        for type, index, val in reversed(queries):
            if index not in vis[type]:  # 后面（>i）没有对这一行/列的操作
                # 这一行/列还剩下 n-len(vis[type^1]) 个可以填入的格子
                ans += (n - len(vis[type ^ 1])) * val
                vis[type].add(index)  # 标记操作过
        return ans

思路来源