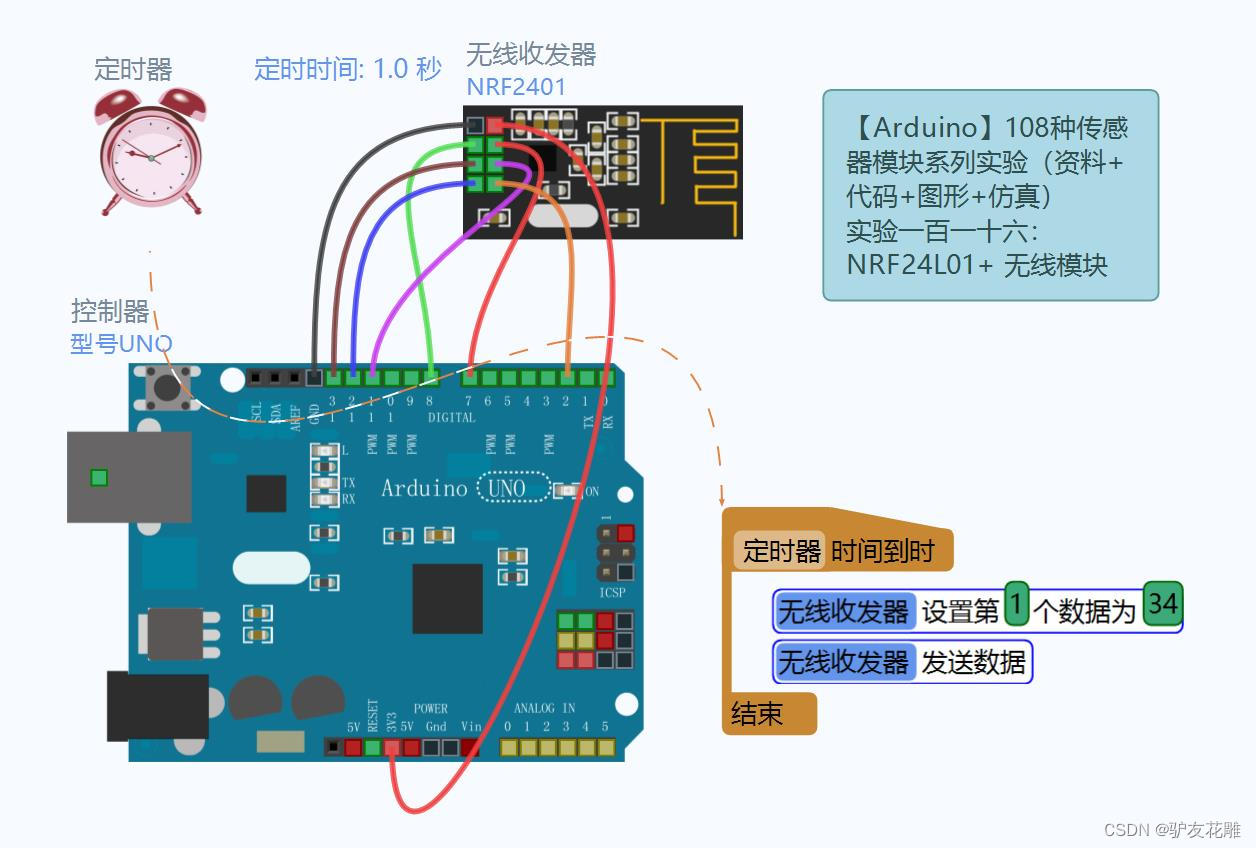
为了更好的阅读体检,为了更好的阅读体检,,可以查看我的算法学习博客第三题-交通规划
在线评测链接:P1237
题目内容
塔子哥所在的国家有 n 个城市,这 n 个城市排成一列,按顺序编号为 1,2,3,...,n。然而,由于历史原因和地理条件等多种原因,这些城市之间并没有相互连接的铁路,导致交通十分不便。
为了改善这种情况,政府决定修建一些铁路来提高城市之间的交通效率。具体来说,政府计划在未来的 T 天内进行一系列铁路建设工作。每一天,政府会进行如下操作之一:
-
L x:在编号为 x 的城市和其左边的城市之间修建一条铁路,以便两个城市之间的交通更加便利。如果 x 已经位于最左边,或者 x 和它左边的城市之间已经存在铁路,则该操作无效。 -
R x:在编号为 x 的城市和其右边的城市之间修建一条铁路,以便两个城市之间的交通更加便利。如果 x 已经位于最右边,或者 x 和它右边的城市之间已经存在铁路,则该操作无效。 -
Q x:查询从编号为 x 的城市出发,最远能够到达的向左和向右的城市的编号。
塔子哥需要编写一段程序来模拟这一系列操作,并及时输出每个 Q x 操作的结果。通过这个程序,政府可以更加高效地规划城市之间的交通网络,从而促进经济和社会的发展。
输入描述
第一行输入两个正整数 n , T ; 接下来 T 行,每行输入形如题面中的其中一种。
,
,
输出描述
对于每一个Q x 操作,输出一行两个正整数,分别表示 x 往左边和往右边最远能到达的城市编号中间用空格隔开。
样例
输入
3 5 Q 2 L 2 Q 2 R 2 Q 2
输出
2 2 1 2 1 3
思路
并查集
考虑将n个城市看成图上的n个节点。那么
-
每次将两个城市之间连通,相当于在点 u 和点 v 之间连一条边
-
每次查询一个城市可以向左和向右到达的最远城市,这启发我们并查集合并时需要维护两个值,一个合并时总是指向值更小的,一个合并时总是指向值更大的。即维护集合最大最小值
知识点学习:并查集
完全没接触过或不太熟悉并查集的同学,可以参考以下学习路线:
1.并查集算法讲解 -C++实现
图论——并查集(详细版)
看完本视频之后对并查集先有一个初步的了解
2.刷题
根据塔子哥给出的类似题目推荐,刷完Leetcode的相关题目以及CodeFun2000相关题目推荐
3.进阶应用(偏竞赛难度)
如果对并查集的应用有比较大的兴趣,希望进一步接触更多更妙的内容,可以学习
1.OI-WIKI-并查集应用
2.百度搜集ATC,CF以及ICPC/CCPC区域赛真题
类似题目推荐
Leetcode
-
547. 朋友圈
-
130. 被围绕的区域
-
200. 岛屿数量
-
684. 冗余连接
-
323. 无向图中连通分量的数目
CodeFun2000
以下问题用BFS/DFS解决都能解决。为了更好的学习并查集,希望大家能够尽量使用并查集完成
1.P1147 阿里巴巴 2023.4.3-研发岗-第二题-又一个连通块数数题
2.P1094. 米哈游 2023.03.19-第一题-塔子哥的RBG矩阵
时间复杂度:O(n\log n)
代码
CPP
#include <bits/stdc++.h>
using namespace std;
const int N = 10010;
// pL:维护集合最小值 , pR:最大值
int pL[N], pR[N];
int n, m;
char op[2];
int num;
// 并查集 非递归写法
int find(int p[], int x) {
int root = x;
while (root != p[root]) root = p[root];
while (x != p[x]) {
int nx = p[x];
p[x] = root;
x = nx;
}
return root;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) pL[i] = pR[i] = i;
// 模拟
for (int i = 1; i <= m; ++i) {
scanf("%s%d", op, &num);
if (*op == 'L') {
if (num == 1) continue;
int pa = find(pL, num - 1), pb = find(pL, num);
if (pa == pb) continue ;
pL[pb] = pa;
pa = find(pR, num - 1), pb = find(pR, num);
pR[pa] = pb;
} else if (*op == 'R') {
if (num == n) continue ;
int pa = find(pL, num), pb = find(pL, num + 1);
if (pa == pb) continue ;
pL[pb] = pa;
pa = find(pR, num), pb = find(pR, num + 1);
pR[pa] = pb;
} else {
printf("%d %d\n", find(pL, num), find(pR, num));
}
}
return 0;
}
Java
import java.util.Objects;
import java.util.Scanner;
public class Main {
static int N = 100010;
// pL:维护集合最小值 , pR:最大值
static int[] pL = new int[N];
static int[] pR = new int[N];
static Scanner sc = new Scanner(System.in);
// 并查集 : 寻找父亲
static int find(int[] p, int x) {
if (x != p[x]) p[x] = find(p, p[x]);
return p[x];
}
public static void main(String[] args) {
int n = sc.nextInt();
int m = sc.nextInt();
for (int i = 1; i <= n; ++i) pL[i] = pR[i] = i;
// 模拟
for (int i = 0; i < m; ++i) {
String op = sc.next();
int x = sc.nextInt();
if ("Q".equals(op)) {
int L = find(pL, x);
int R = find(pR, x);
System.out.println(L + " " + R);
} else if ("L".equals(op)) {
if (x == 1) continue;
int pa = find(pL, x - 1);
int pb = find(pL, x);
if (pa == pb) continue;
pL[pb] = pa;
pa = find(pR, x - 1);
pb = find(pR, x);
if (pa == pb) continue;
pR[pa] = pb;
} else {
if (x == n) continue;
int pa = find(pL, x);
int pb = find(pL, x + 1);
if (pa == pb) continue;
pL[pb] = pa;
pa = find(pR, x);
pb = find(pR, x + 1);
if (pa == pb) continue;
pR[pa] = pb;
}
}
}
}
Python
n, T = map(int, input().split()) f = [i for i in range(n+1)] # mi维护集合最小值 , mx 维护 最大值 mi = [i for i in range(n+1)] mx = [i for i in range(n+1)] # 并查集 模板 def find(x): global f if f[x] == x: return x f[x] = find(f[x]) return f[x] def mer(x, y): global f x = find(x) y = find(y) if x != y: f[x] = y mx[y] = max(mx[x], mx[y]) mi[y] = min(mi[x], mi[y]) for ii in range(T): p, x = input().split() x = int(x) if p == 'L' and x != 1: mer(x, x-1) if p == 'R' and x != n: mer(x, x+1) if p == 'Q': x = find(x) print(mi[x], mx[x])
Go
package main
import (
"fmt"
)
var f []int
var mi []int
var mx []int
func main() {
var n, T int
fmt.Scan(&n, &T)
// f: 父亲
f = make([]int, n+1)
// mi mx 维护每个点所在集合的最大值最小值
mi = make([]int, n+1)
mx = make([]int, n+1)
// 初始化 指向自己
for i := 0; i <= n; i++ {
f[i] = i
mi[i] = i
mx[i] = i
}
// 模拟
for i := 0; i < T; i++ {
var p string
var x int
fmt.Scan(&p, &x)
if p == "L" && x != 1 {
mer(x, x-1)
}
if p == "R" && x != n {
mer(x, x+1)
}
if p == "Q" {
x = find(x)
fmt.Println(mi[x], mx[x])
}
}
}
// 并查集 模板
func find(x int) int {
if f[x] == x {
return x
}
f[x] = find(f[x])
return f[x]
}
func mer(x, y int) {
x = find(x)
y = find(y)
if x != y {
f[x] = y
mx[y] = max(mx[x], mx[y])
mi[y] = min(mi[x], mi[y])
}
}
// 最大最小值
func max(a, b int) int {
if a > b {
return a
}
return b
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
Js
process.stdin.resume();
process.stdin.setEncoding('utf-8');
let input = '';
process.stdin.on('data', (data) => {
input += data;
});
process.stdin.on('end', () => {
lines = input.trim().split('\n');
let f = []
let mi = []
let mx = []
const arr = lines[0].split(' ')
const n = parseInt(arr[0])
const T = parseInt(arr[1])
// mi mx 维护每个点所在集合的最大值最小值
for (let i = 0; i <= n; i++) {
f[i] = i
mi[i] = i
mx[i] = i
}
// 并查集模板
function find(x) {
if (f[x] === x) {
return x
}
f[x] = find(f[x])
return f[x]
}
function mer(x, y) {
x = find(x)
y = find(y)
if (x !== y) {
f[x] = y
mx[y] = Math.max(mx[x], mx[y])
mi[y] = Math.min(mi[x], mi[y])
}
}
// 模拟
for (let i = 1; i <= T; i++) {
const line = lines[i].trim().split(' ')
const p = line[0]
const x = parseInt(line[1])
if (p === 'L' && x !== 1) {
mer(x, x-1)
}
if (p === 'R' && x !== n) {
mer(x, x+1)
}
if (p === 'Q') {
const res = find(x)
console.log(mi[res], mx[res])
}
}
});


![[C++刷题之旅]反转链表](https://img-blog.csdnimg.cn/b51033cc0360463f80e1dd2c2e0ba3ef.png)