在神经网络中,使用前向或者反向传播计算后,再使用梯度下降去寻找代价函数最小时 θ \theta θ的取值是一个可行的方法,但是它很容易出错:因为在这个算法中含有海量的细节,容易产生微小而又难以察觉的bug。即便是存在bug,梯度下降计算出来的 J ( θ ) J(\theta) J(θ)还是会照常迭代下降,但是得出来的结果的误差将会比正确的情况高出一个量级。因此我们需要使用梯度检验的方法赖解决这种问题,只要需要使用类似梯度下降或者反向传播的算法都可以使用这种方法,这种方法能够确保你的前向\反向传播完全正确。
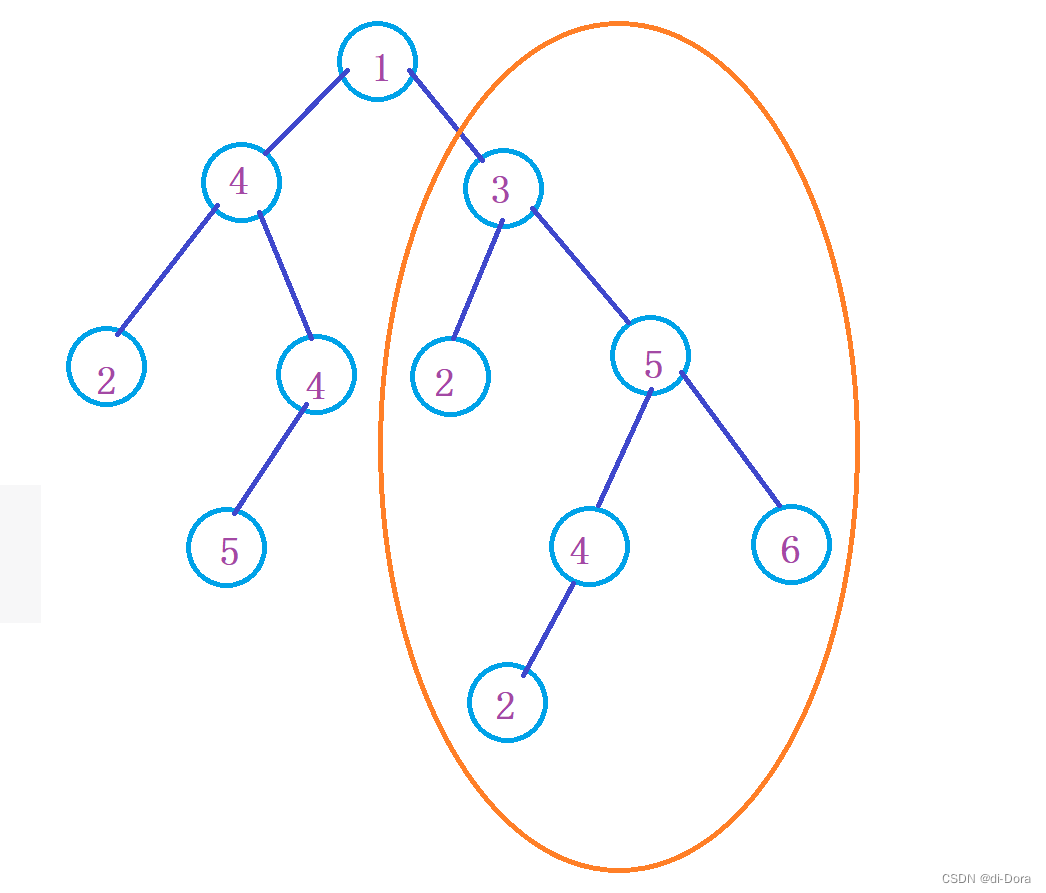
首先我们以下图为例子,其中有一个点
θ
\theta
θ,而
ϵ
\epsilon
ϵ是一个很小的数,类似于微积分中的微小增量,一般可以将
ϵ
\epsilon
ϵ取作
1
0
−
4
10^{-4}
10−4
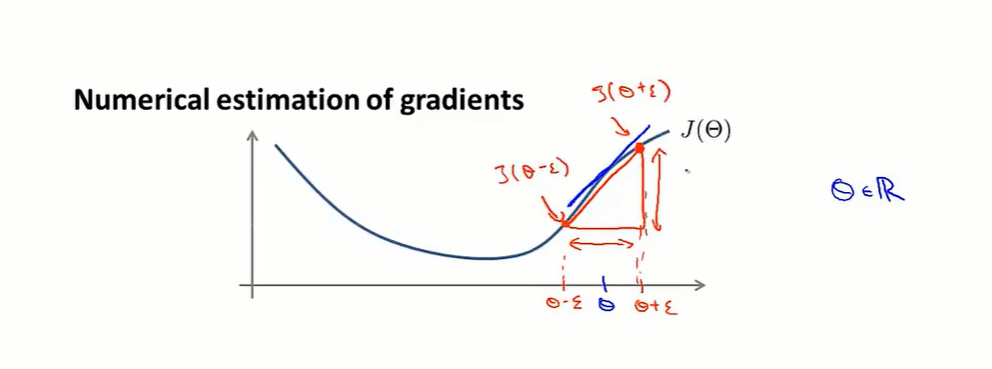
而另外两个点分别为
(
θ
−
ϵ
,
J
(
θ
−
ϵ
)
)
(\theta-\epsilon , J(\theta-\epsilon ))
(θ−ϵ,J(θ−ϵ))和
(
θ
+
ϵ
,
J
(
θ
+
ϵ
)
)
(\theta+\epsilon , J(\theta+\epsilon ))
(θ+ϵ,J(θ+ϵ)),这和导数十分像不是吗?那当然我们可以得出如下的式子
δ
δ
θ
J
(
θ
)
≈
g
r
a
d
A
p
p
r
o
x
=
J
(
θ
+
ϵ
)
−
J
(
θ
−
ϵ
)
2
ϵ
\frac{\delta }{\delta \theta } J(\theta )\approx gradApprox= \frac{J(\theta+\epsilon )-J(\theta-\epsilon )}{2\epsilon }
δθδJ(θ)≈gradApprox=2ϵJ(θ+ϵ)−J(θ−ϵ)
接下来我们呢考虑更加广泛的情况比如假设
θ
\theta
θ是一个n维向量,也就是
θ
∈
R
n
,
θ
=
[
θ
1
,
θ
2
,
θ
3
,
.
.
.
,
θ
n
]
\theta \in R^n,\theta=[\theta_1,\theta_2,\theta_3,...,\theta_n]
θ∈Rn,θ=[θ1,θ2,θ3,...,θn],那么我们可以使用相同的办法得出对应偏导数的大约值

接下来我们需要使用到反向传播所计算出来的导数向量
D
V
e
c
=
[
D
(
1
)
,
D
(
2
)
,
D
(
3
)
.
.
.
D
(
n
)
]
D\:Vec=[D^{(1)},D^{(2)},D^{(3)}...D^{(n)}]
DVec=[D(1),D(2),D(3)...D(n)],检查
g
r
a
d
A
p
p
r
o
x
≈
D
V
e
c
gradApprox\approx D\:Vec
gradApprox≈DVec,如果成立的话,则可以认为反向传播是正确的,把DVex用于梯度下降则可以得出较好的结果
主要的步骤如下: