文章目录
- AI实战营第二期 第九节 《底层视觉与MMEditing》
- 什么是超分辨率
- 图像分辨率的目标
- 应用方向
- 超分的类型
- 单图超分的解决思路
- 深度学习时代的超分辨率算法
- SRCNN
- Fast SRCNN
- SRResNet
- 感知损失 VS. 均方误差
- 均方误差
- 感知损失
- 对抗生成网络
- GAN应用于超分辨率
- 如何学习生成器网络
- 对抗训练
- GAN优化目标
- DCGAN
- SRGAN
- ESRGAN
- 视频复原任务流程
- EDVR
- BasicVSR
AI实战营第二期 第九节 《底层视觉与MMEditing》

本节内容 :
- 图像超分辨率 Super Resolution
- 基于卷积网络的模型 SRCNN 与 FSRCNN
- 损失函数
- 对抗生成网络 GAN 简介
- 基于 GAN 的模型 SRGAN 与 ESRGAN
- 视频超分辨率介绍
- 实践 MMEditing 1
什么是超分辨率
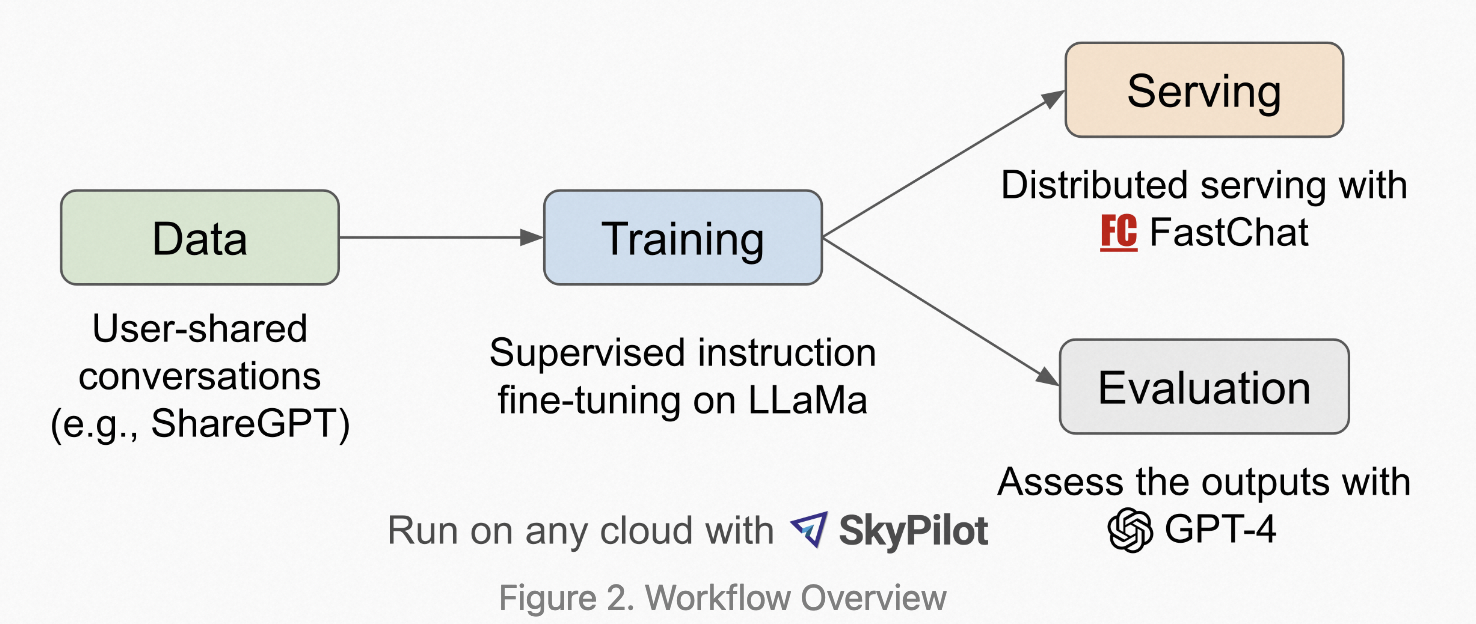
图像超分辨率 : 根据从低分辨率图像重构高分辨率图像 。 将图像放大,变清晰

图像分辨率的目标
- 提高图像的分辨率
- 高分图像符合低分图像的内容
- 恢复图像的细节、产生真实的内容
常用的双线性或双立方揷值不能恢复图像的高频细节

应用方向
经典游戏高清重制

动画高清重制

照片修复

节约高清视频传输带宽

民生领域,如:医疗影像,卫星影像,监控系统 (车牌或人脸),空中监察等。
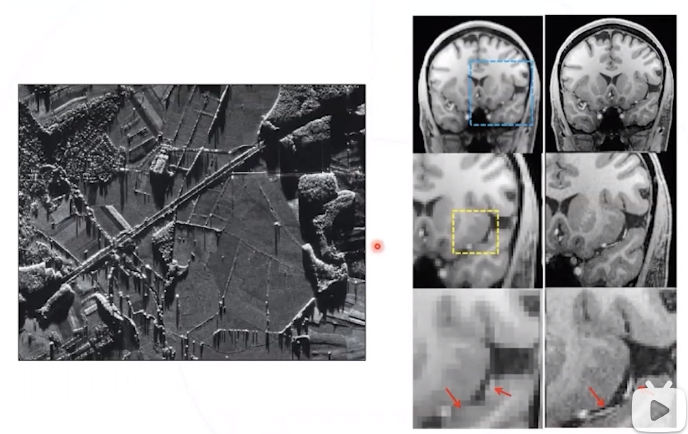
超分的类型

单图超分的解决思路
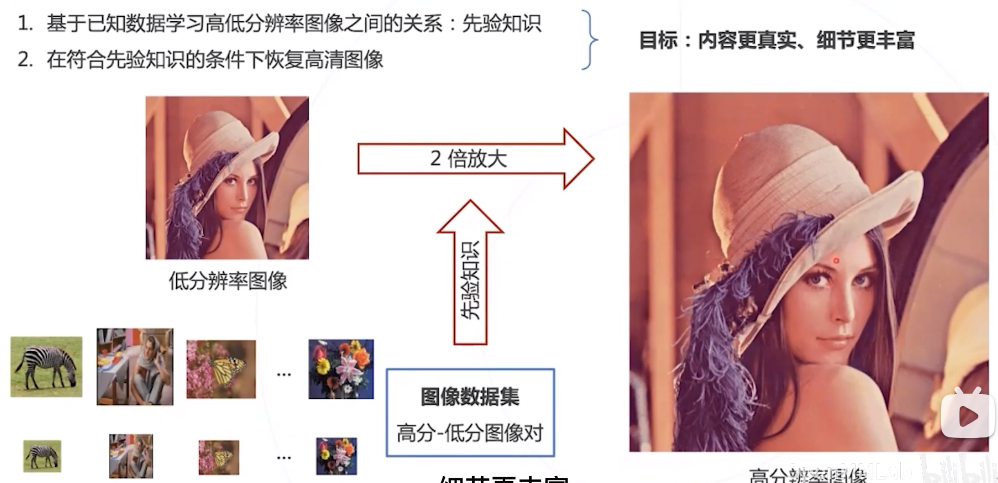
经典的解决方法:稀疏编码 ,一种无监督的方法。
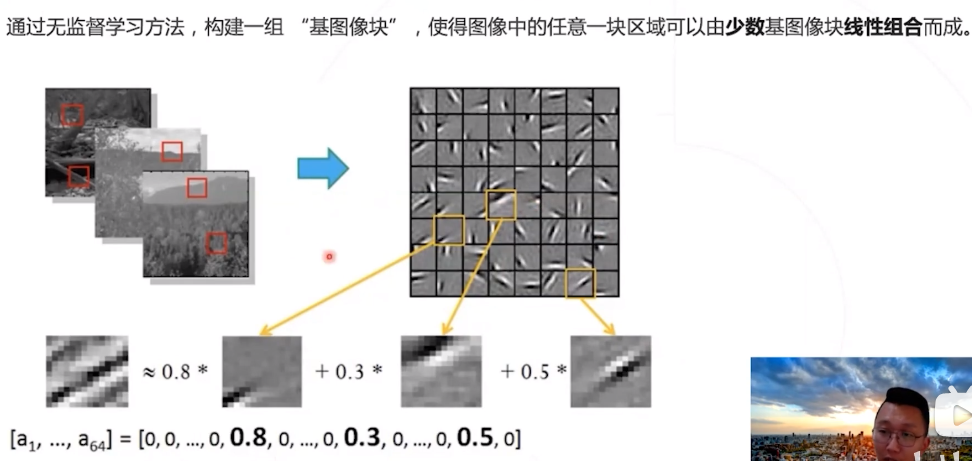
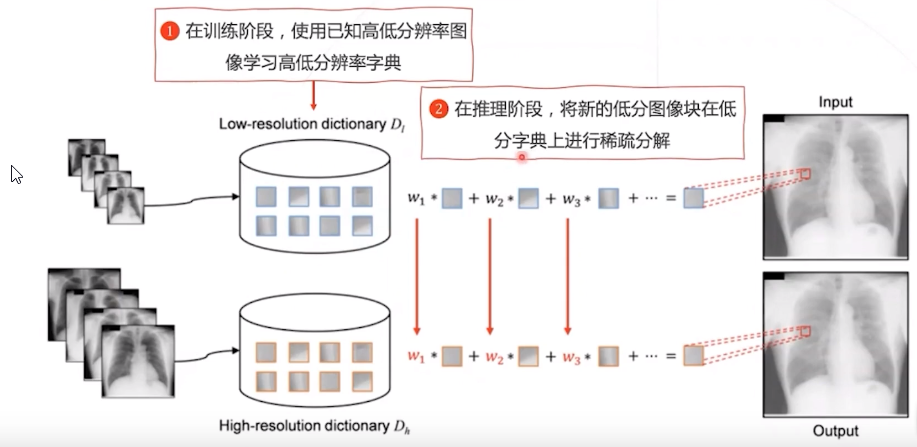
缺点:即便已经学习出字典,对低分辨率图像块进行系数分解、得到系数仍然是一个相对复杂的优化问题。而且训练和推理都很耗时!

深度学习时代的超分辨率算法
- 基于卷积网络和普通损失函数
使用卷积神经网络,端到端从低分辨率图像恢复高分辨率图像
代表算法 : SRCNN 与 FSRCNN - 使用生成对抗网络
采用生成对抗网络的策略,鼓励产生细节更为真实的高分辨率图像。
代表算法: SRGAN 与 ESRGAN
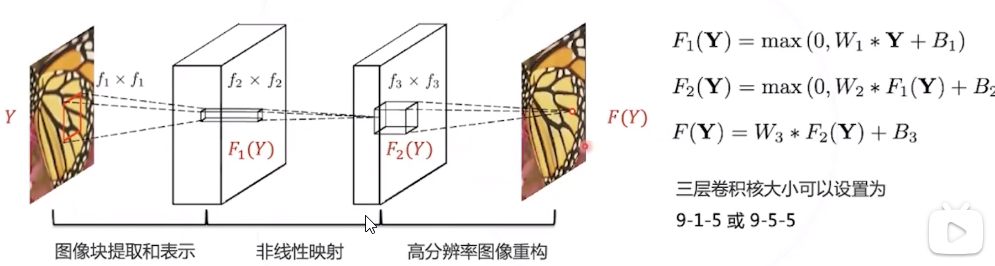
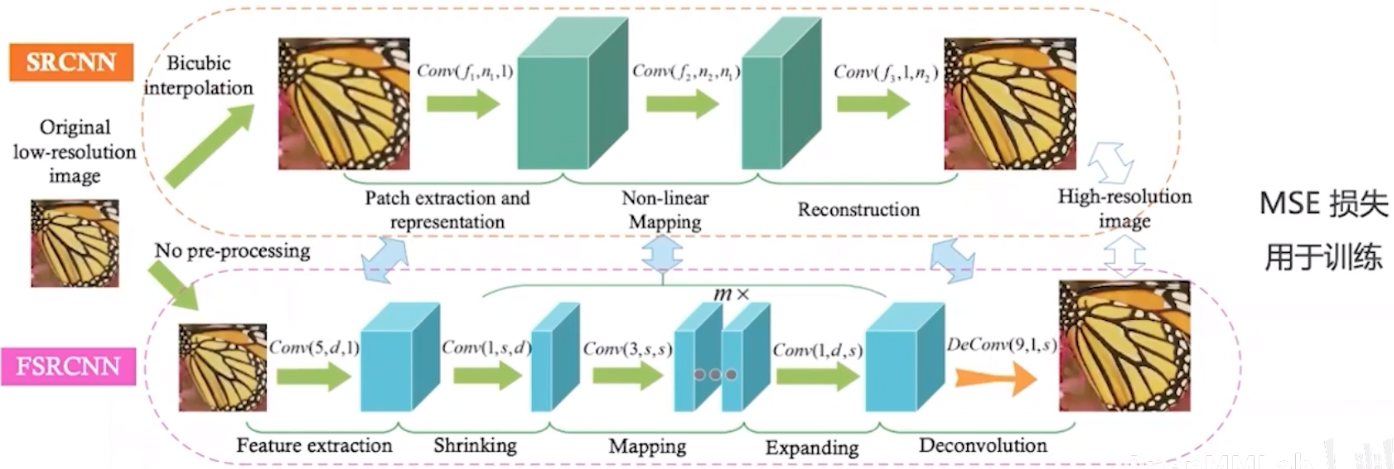
SRCNN
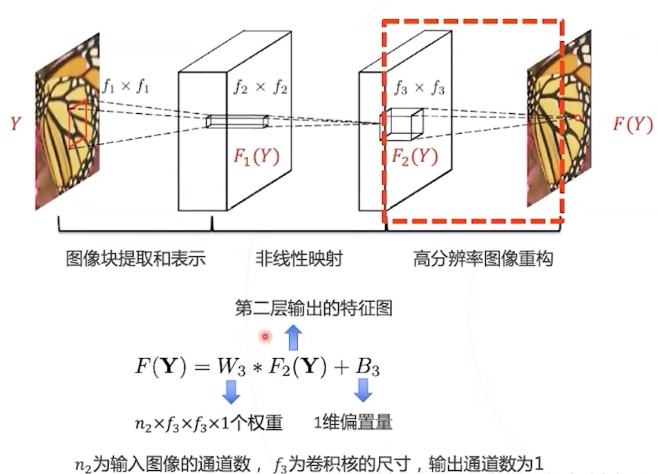
SRCNN 是首个基于深度学习的超分辨率算法,证明了深度学习在底层视觉的可行性。 模型仅由三层卷积层构成构成,可以端到端学习,不需要额外的前后处理步骤。
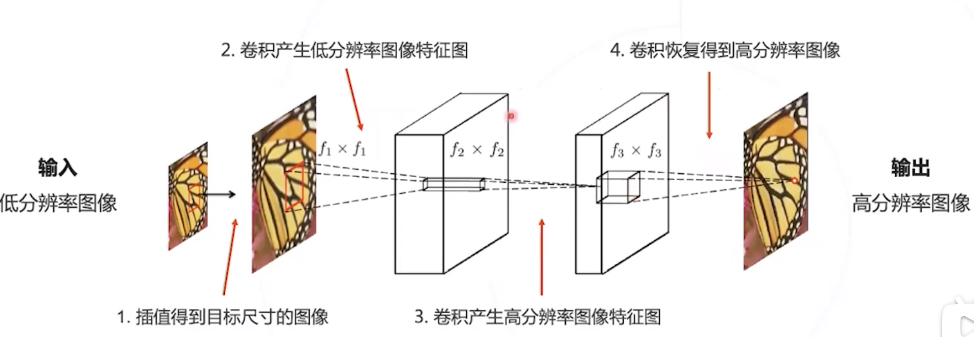
SRCNN 的单个卷积层有明确的物理意义 :
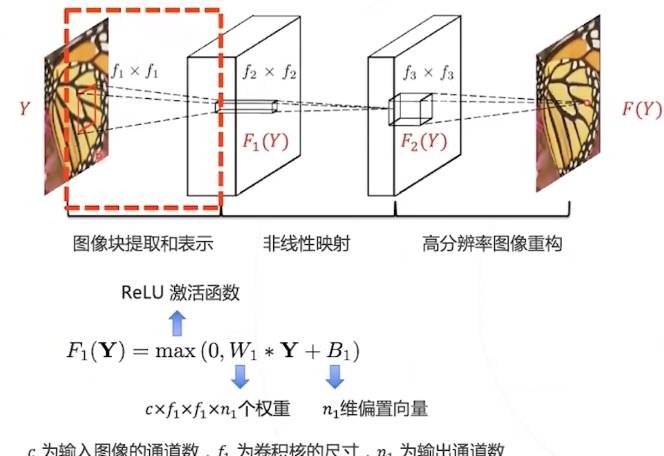
第一层 : 提取图像块的低层次局部特征;
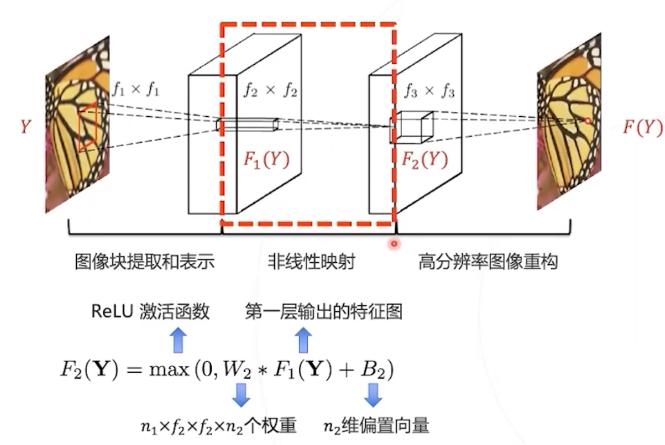
第二层 : 对低层次局部特征进行非线性变换,得到高层次特征;
第三层 : 组合邻域内的高层次特征,恢复高清图像。
经典方法通常将图像切分成小块, 并基于一系列基底对图像块进行分 解 (常用算法有PCA、DCT、 Haar小波等 ),分解系数向量即 为图像块在基底上的表示。
这个操作等价于用一系列卷积核 (对应经典方法中的基底) 对原图 像进行卷积。
F
1
(
Y
)
F_{1}(Y)
F1(Y) 中每个像素位 置上的
n
1
n_{1}
n1 维度的向量即为对应图 像块在基底上的表示。
使用神经网络,基底可以从数据中学习出来。
在 ImageNet 数据集上训练的 SRCNN 可以学习到不同的低层次特征所对应的卷积核。

第二层:非线性映射
f
2
=
1
f_{2}=1
f2=1 时,第二层卷积将
F
1
(
Y
)
F_{1}(Y)
F1(Y) 每 个位置上
n
1
n_{1}
n1 维度的特征非线性映射 为一个
n
2
n_{2}
n2 维的特征。
该特征可以看作是图像块在高分基 底上的表示,在后一层中用于重 构。
非线性映射可以有很多层,但实验 表明只应用单层卷积层就可以达到 较好的效果
第三层:图像重构
第三层的卷积核对应高分辨率基 底,用 F_{2}(Y) 中的系数对高分基底 加权求和即可得到高分图像块。第 三层卷积完成这个过程。
三个步骤与稀疏编码方法中的步骤一一对应。
准备数据:
将 ImageNet 数据集中的图像作为高分图像,降采样再揷值升采样得到的图像作为低分图像
需要学习的参数 :
Θ
=
{
W
1
,
W
2
,
W
3
,
B
1
,
B
2
,
B
3
}
\Theta=\left\{W_{1}, W_{2}, W_{3}, B_{1}, B_{2}, B_{3}\right\}
Θ={W1,W2,W3,B1,B2,B3}
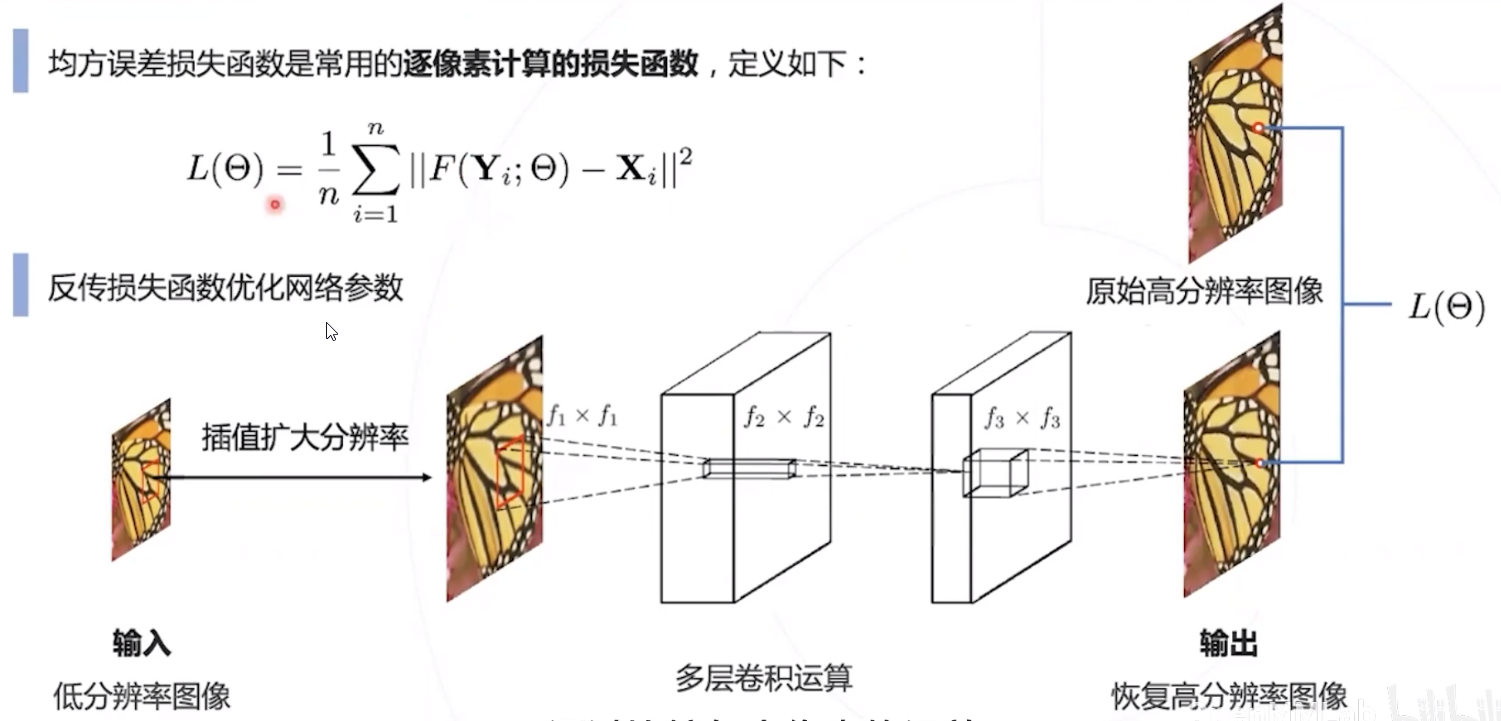
损失函数 : 逐像素计算恢复图像和原高分图像的平方误差 (Mean Squared Error, MSE)
L ( Θ ) = 1 n ∑ i = 1 n ∥ F ( Y i ; Θ ) − X i ∥ 2 , 最小化损失函数即可鼓励网络完美恢复高分辨率图像 L(\Theta)=\frac{1}{n} \sum_{i=1}^{n}\left\|F\left(\mathbf{Y}_{i} ; \Theta\right)-\mathbf{X}_{i}\right\|^{2}, \quad \text { 最小化损失函数即可鼓励网络完美恢复高分辨率图像 } L(Θ)=n1i=1∑n∥F(Yi;Θ)−Xi∥2, 最小化损失函数即可鼓励网络完美恢复高分辨率图像
通过标准的 SGD 训练模型
Δ
i
+
1
=
0.9
⋅
Δ
i
−
η
⋅
∂
L
∂
W
i
ℓ
,
W
i
+
1
ℓ
=
W
i
ℓ
+
Δ
i
+
1
\Delta_{i+1}=0.9 \cdot \Delta_{i}-\eta \cdot \frac{\partial L}{\partial W_{i}^{\ell}}, \quad W_{i+1}^{\ell}=W_{i}^{\ell}+\Delta_{i+1}
Δi+1=0.9⋅Δi−η⋅∂Wiℓ∂L,Wi+1ℓ=Wiℓ+Δi+1
评估
P S N R = 10 ⋅ log 10 ( M A X I 2 M S E ) P S N R=10 \cdot \log _{10}\left(\frac{M A X_{I}^{2}}{M S E}\right) PSNR=10⋅log10(MSEMAXI2)
峰值信噪比 (Peak signal-to-noise ratio, PSNR) 为最大信号能量与平均 噪声能量的比值,值越大恢复效果越 好。
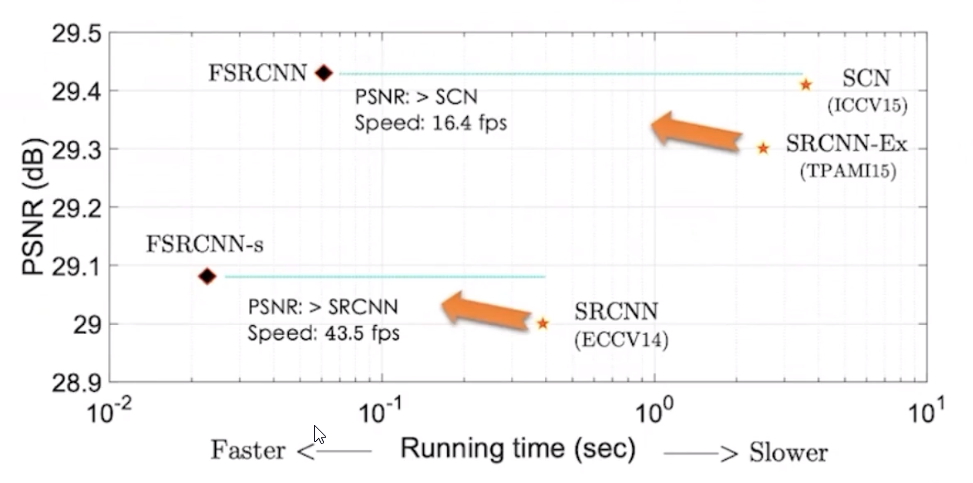
SRCNN 在性能和速度上全面超越深 度学习前的算法
缺点
SRCNN 先对低分图像进行揷值,再在高分辨率下进行卷积运算; 然而揷值不产生额外信息,因而产生一定的几余计算;
在学术数据集上,SRCNN 的速度在 1 10 FPS,达不到实时的标准。
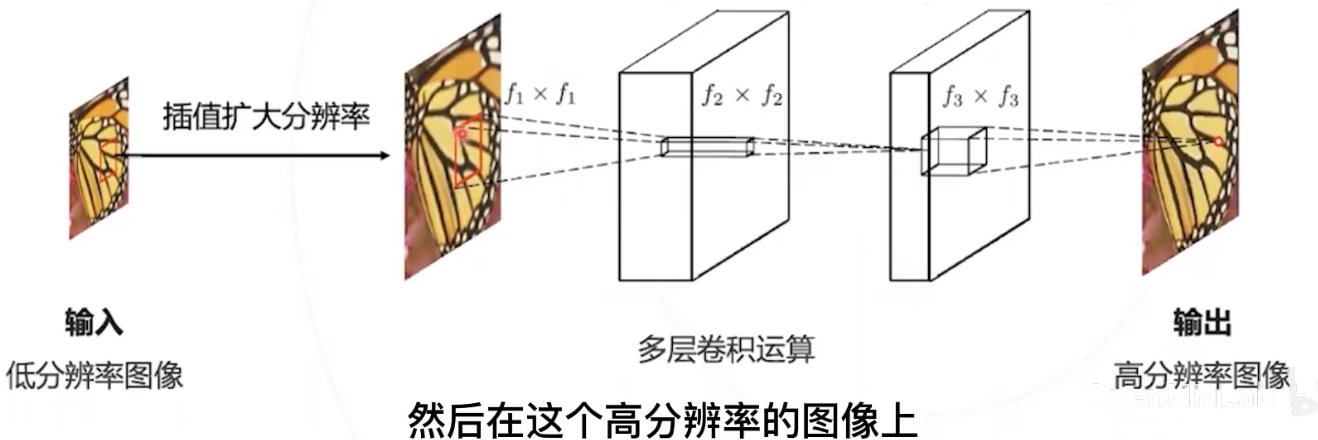
Fast SRCNN
FSRCNN 在 SRCNN 的基础上针对速度进行了改进 :
- 不使用掐值, 直接在低分辨率图像上完成卷积运算, 降低运算量
- 使用 1 × \times × 1 的卷积层对特征图通道进行压缩,进一步降低卷积的运算量
- 若干卷积层后再通过转置卷积层提高图像分辨率
优点 - 基于 CPU 进行推理,速度可以达到实时;
- 在处理不同上采样倍数时,只需要微调反卷积的权重,特征映射层的参数额可以保持不变,大幅加快训 练速度。
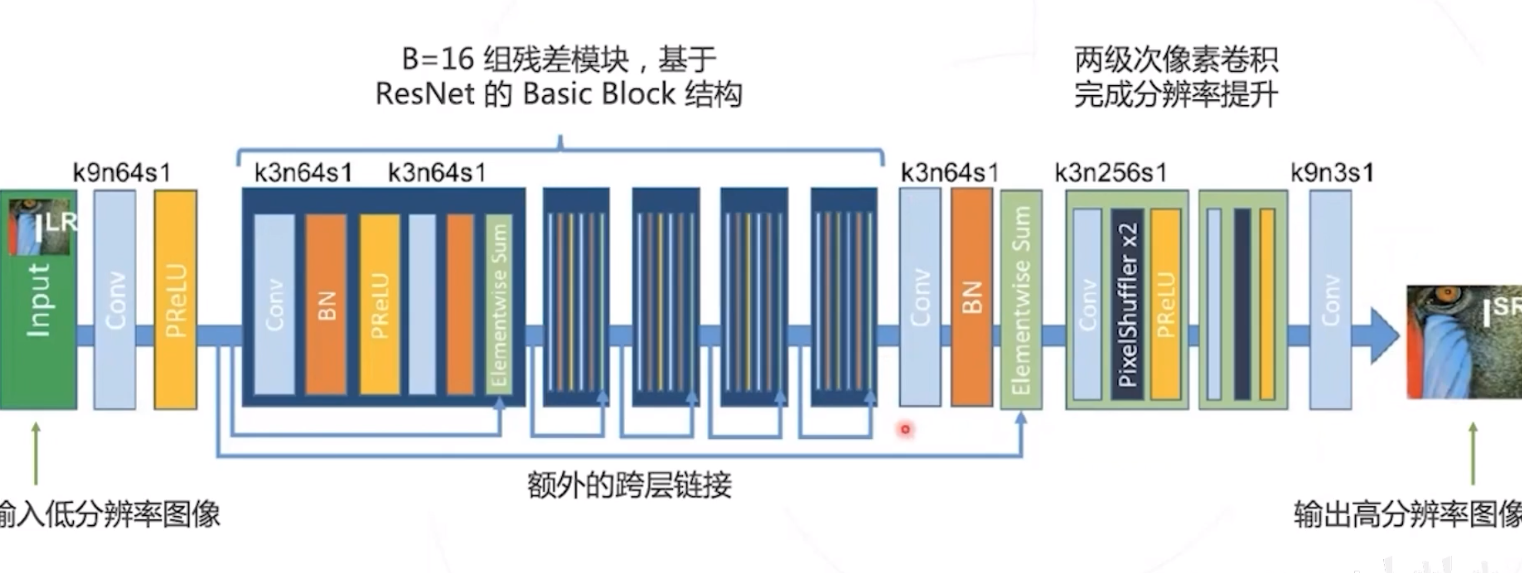
SRResNet
Twitter 于2016年提出的 模型使用类似 ResNet 的网络结构从低分图像生成高分图像。
感知损失 VS. 均方误差
- 逐像素计算的损失函数
比较恢复图像与原始高分图像的每个像素值,并计算均方误差。
例如 : SRCNN 和 FSRCNN 中用到的均方误差损失 (MSE Loss) - 感知损失函数
比较恢复图像与原始高分图像的语义特征,并计算损失。
语义特征的计算由预先训练的神经网络模型给出。例如 : 使用在 ImageNet 数据集上预训诪好的神经网络计算语义特征。
均方误差
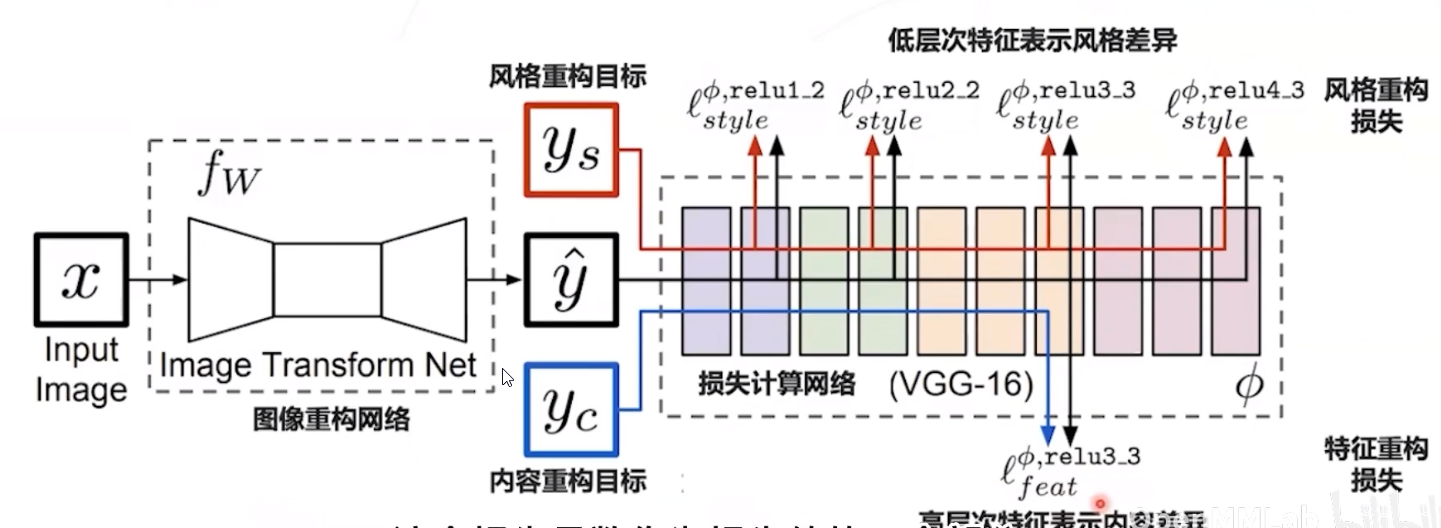
感知损失
比较恢复图像与原始高分图像的语义特征,并计算损失
损失网络一般是训练图像分类任务得到的模型构成,例如 VGG 网络
损失网络不参与学习,在训练过程中参数保持不变
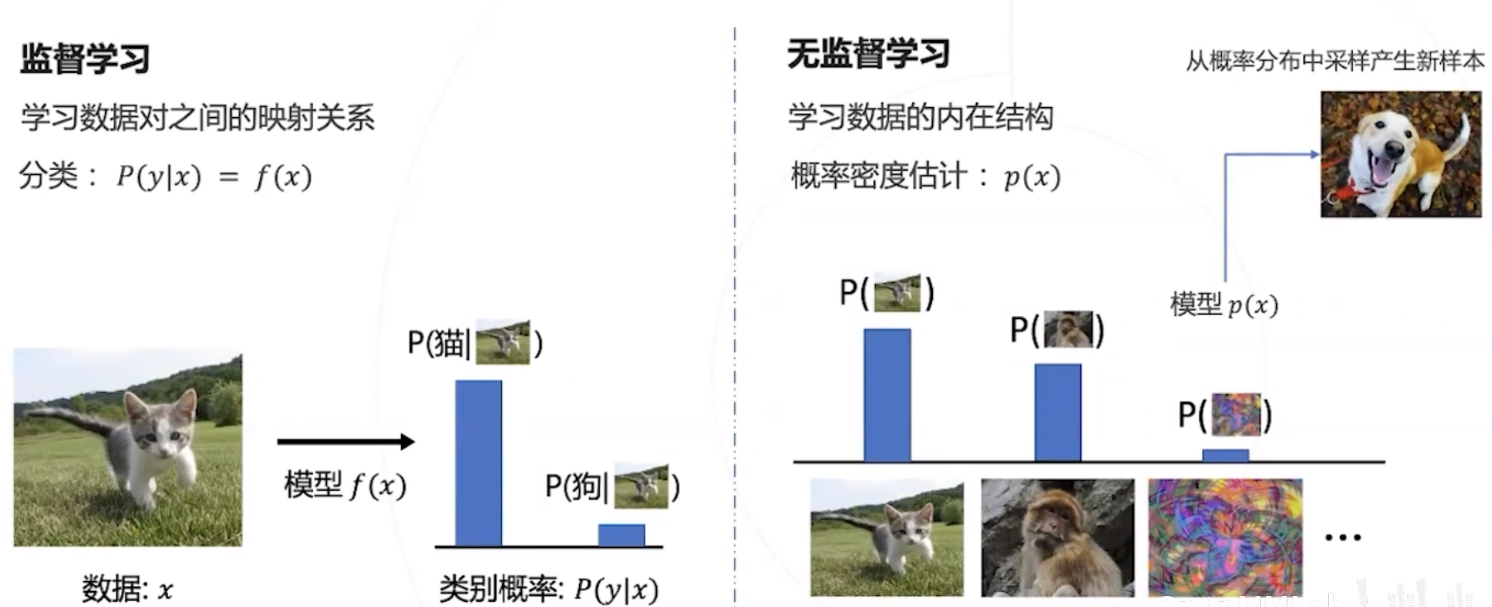
对抗生成网络
对抗生成网络是一种基于神经网络的无监督学习模型,可以建模数据的分布,并通过采样生成新数据。
GAN应用于超分辨率
使用普通损失函数训练的模型细节还有些模糊
使用对抗训练方法训练的模型 细节恢复得更好

如何学习生成器网络
问题 : 我们希望
p
x
p_{x}
px 与
p
d
a
t
a
p_{d a t a}
pdata 近似,但二者没有闭式表达,无法直接计算 “差距” 或损失函数。
思路 : 如果
p
x
p_{x}
px 与
p
d
a
t
a
p_{d a t a}
pdata 有差别,那么它们的样本就可以区分
→
\rightarrow
→ 使用一个分类网络区分两类样本,将分类 正确率作为两个概率分布的“差距”。二者越接近,分类正确率应该越低。
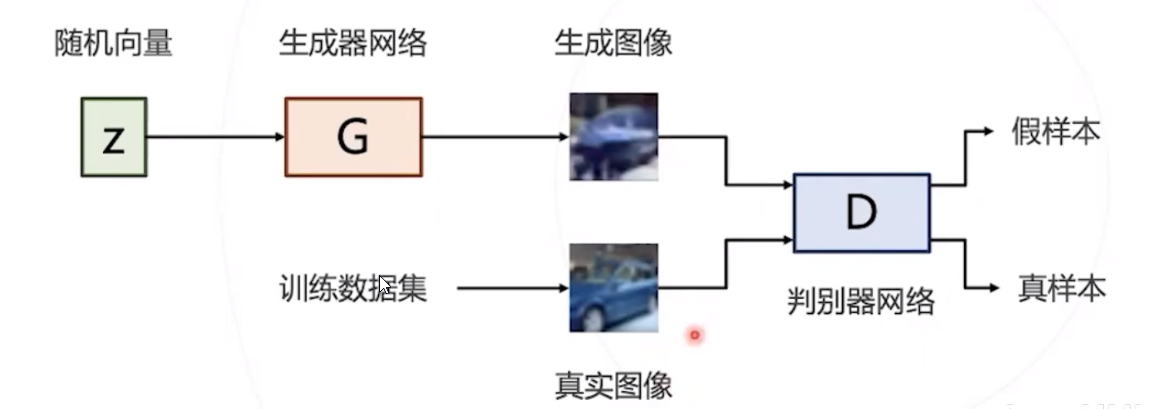
对抗训练
判别器网络 D 和生成器网络 G 采用对抗的方式进行训练 :
- 训练 D 网络时降低分类损失,尽力分辨 G 网络产生的假样本
- 训练 G 网络时提高分类损失,尽力迷惑 D 网络,使之无法区分真假样本
二者相互对抗相互进步,最优状态下 G 网络可以生成以假乱真的样本
GAN优化目标
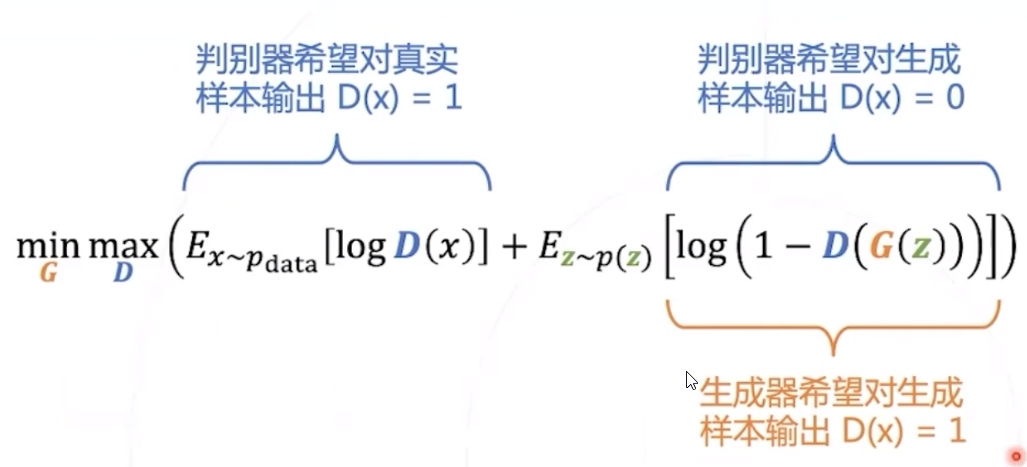
- 对于给定的 G 网络,训练出最佳判别器网络,记录对应的分类损失 (的负值)
- 在所有可能的 G 网络中,找到使得上述损失最大 (对应负值最小 ) 的 G 网络。
- 可以证明,最优 G \mathrm{G} G 网络满足 p G = p data p_{G}=p_{\text {data }} pG=pdata
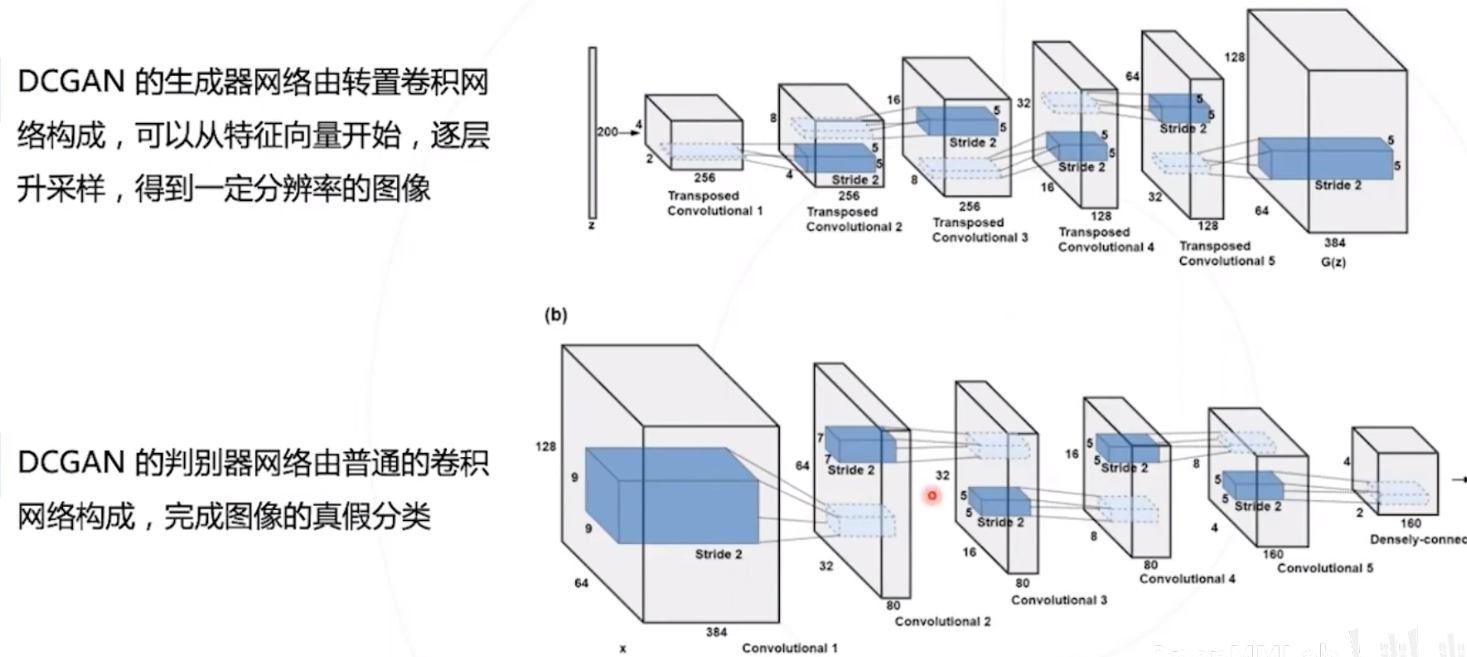
DCGAN
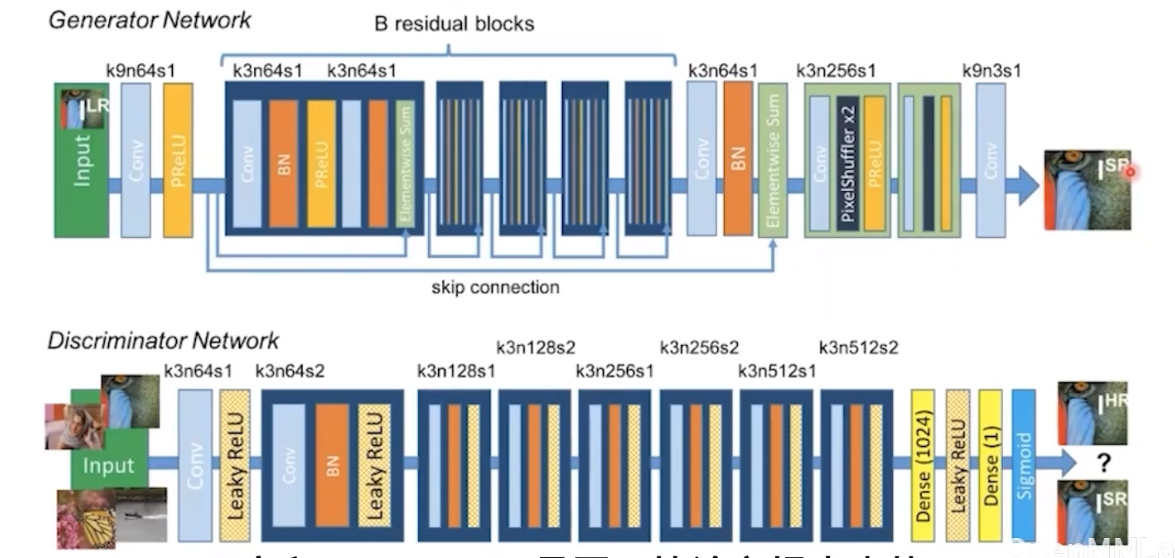
SRGAN
SRGAN 在 SRResNet 的基础上额外增加了判别器网络,用于区分训练集中的高分图像 ( 真实图像 ) 以及 SRResNet 恢复的高分图像 ( 虚假图像 )
ESRGAN
Enhanced SRGAN (ESRGAN) 从网络结构、感知损失、对抗损失三个角度对 SRGAN 进行了全面改进,在超 分辨率效果上取得了很大的提升,同时获得了 PIRM2018 超分辨率挑战赛冠军。

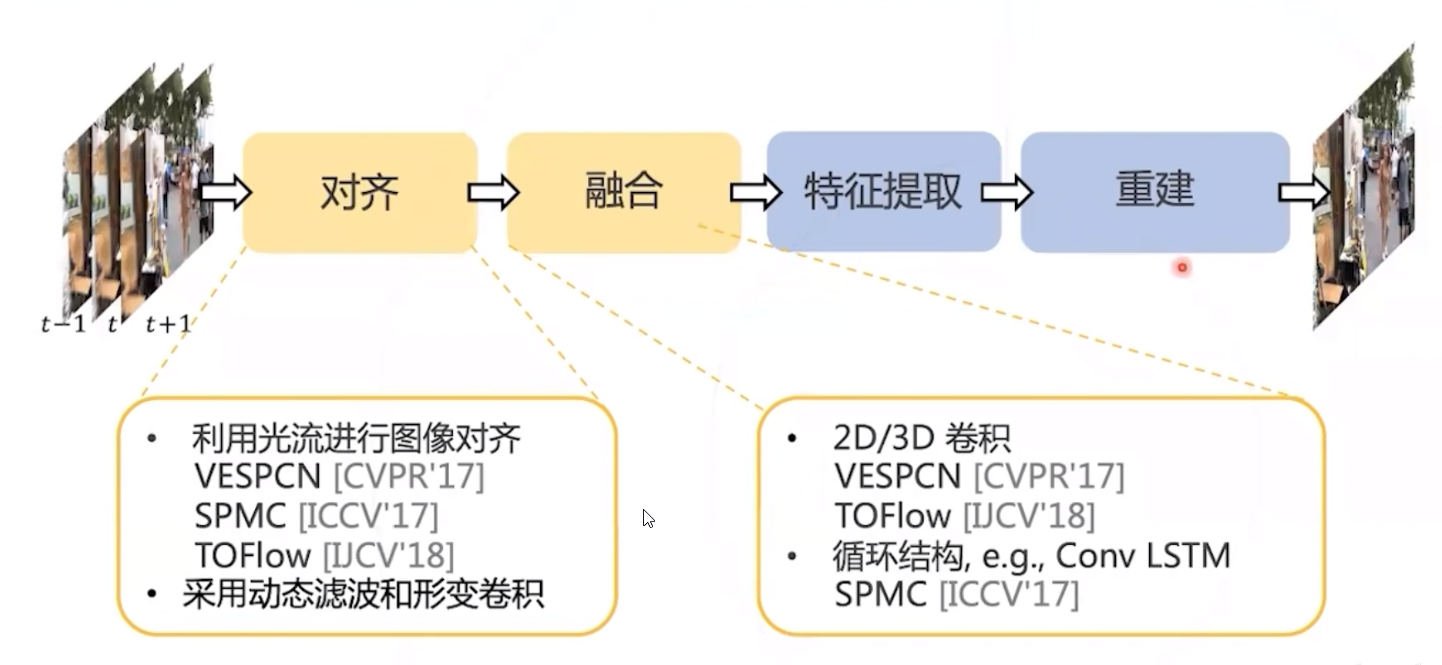
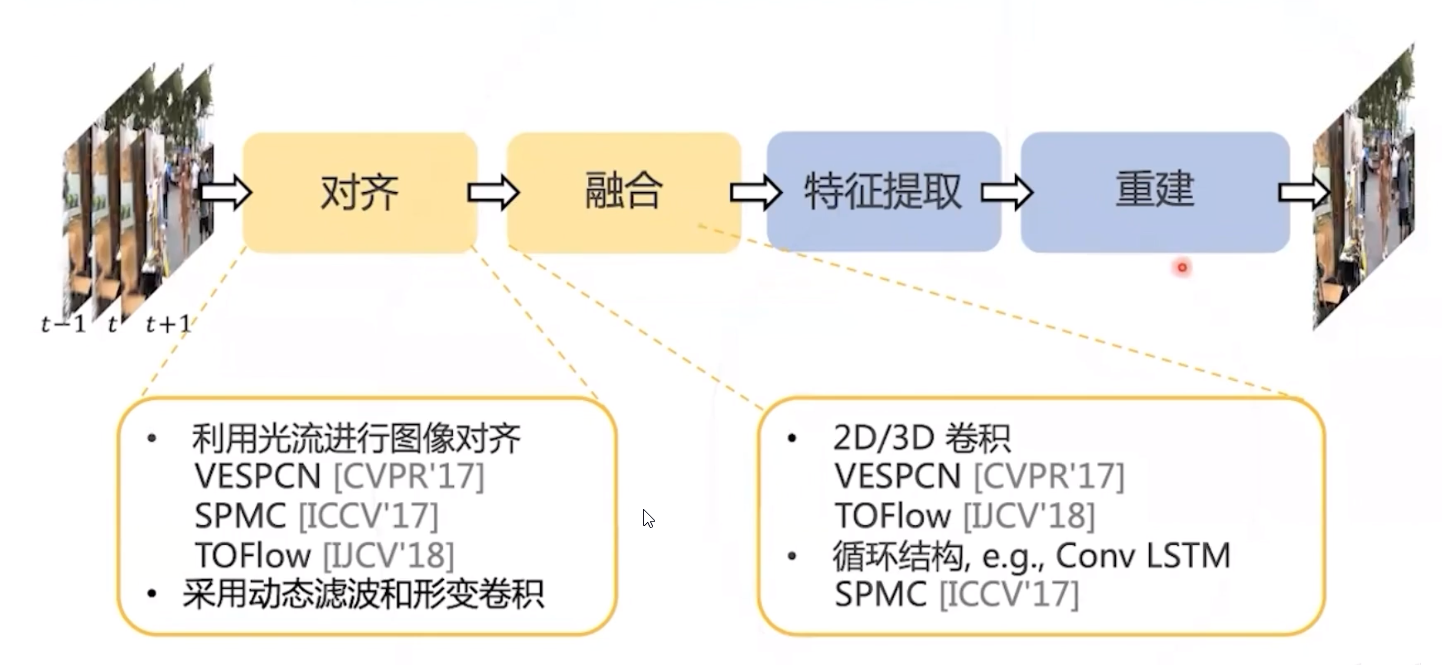
视频复原任务流程
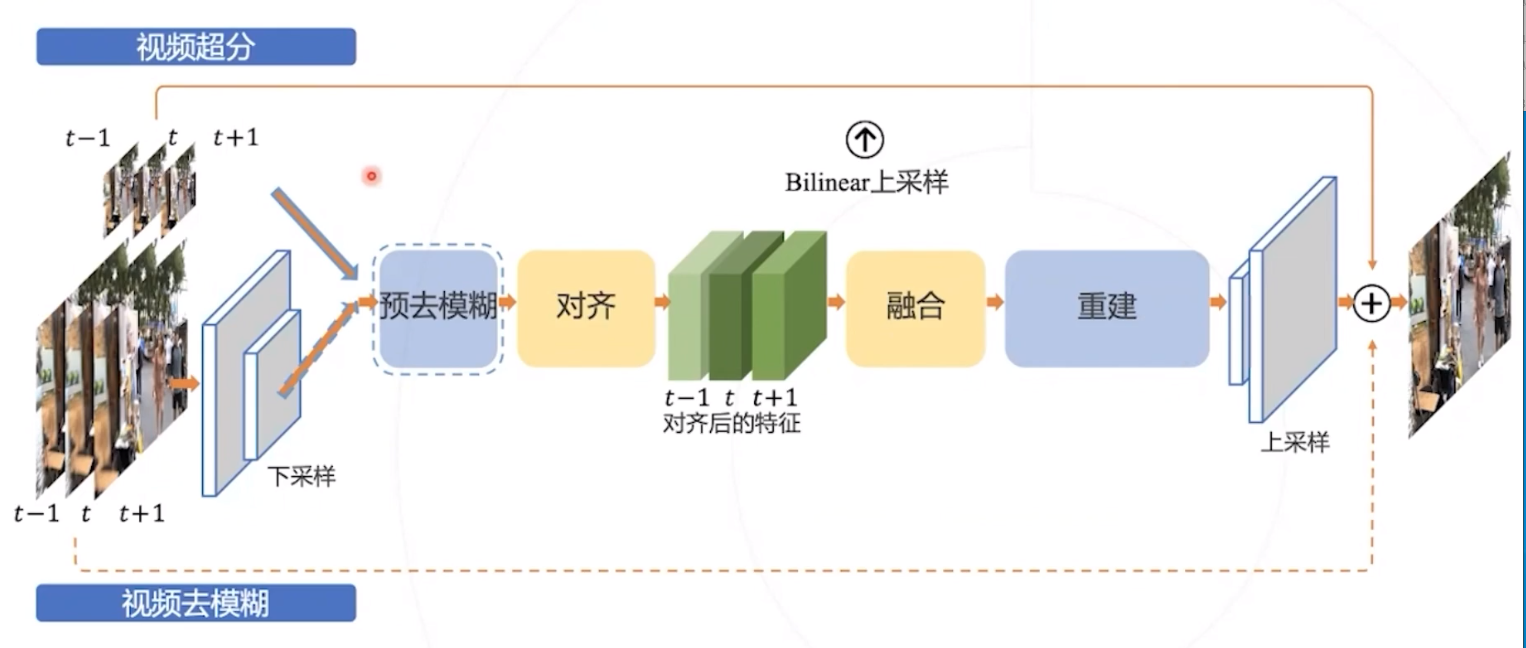
EDVR
- 适用于不同视频复原任务的通用框架
- PCD: 通过金字塔级联变形对齐处理大的运动,使用形变卷积以由粗到细的方式在特征级别进行帧对齐
- TSA: 时空注意力机制
- 由于遮挡,模糊和末对齐等等问题,相邻 帧的信息不足, 不同的相邻帧应该有不同 的权重
- 我们通过以下方式在每帧上分配像素级聚 合权重 :
✓ t e m p o r a l a t t e n t i o n \checkmark temporal attention ✓temporalattention 时间注意机制
✓ s p a t i a l a t t e n t i o n \checkmark spatial attention ✓spatialattention 空间注意机制
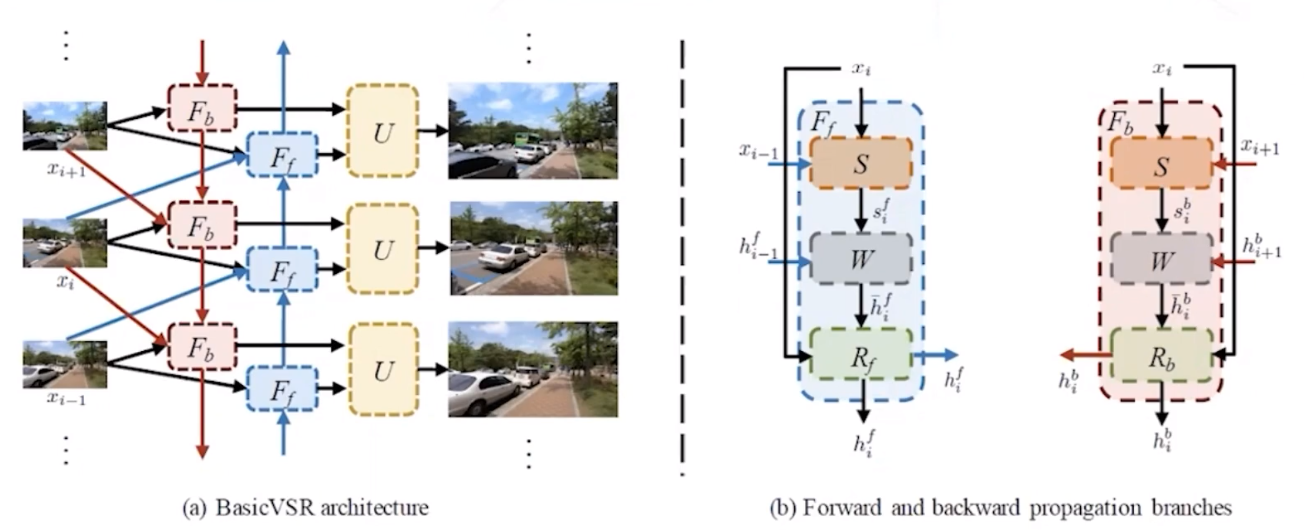
BasicVSR
BasicVSR在结构上更简单,效果比EDVR更好